Sobre a regressão infinita de Russell contra o nominalismo de semelhança

Introdução

Meu objetivo neste ensaio é argumentar que duas réplicas ao argumento de Russell contra o nominalismo de semelhança propostas por Cargile (2003) e Rodriguez-Pereyra (2001; 2002) não funcionam. Para isso procedo da seguinte forma: apresento o argumento de Russell; mostro qual das premissas o nominalista deverá atacar; apresento as respostas nominalistas de Cargile e Rodriguez-Pereyra e mostro por que elas não funcionam.

1. O argumento de Russell

O nominalismo de semelhança apela para relações de semelhança entre particulares a fim de justificar a inexistência de universais. Essa forma de nominalismo defende que aquilo que os universais explicam pode ser explicado somente em termos de relações de semelhança entre particulares. Assim, para explicar a brancura ou a triangularidade de um objeto, por exemplo, o nominalista de semelhança não apelará para a existência de uma entidade diferente dos particulares.

Russell em Os Problemas da Filosofia defende que apelar para a relação de semelhança entre particulares a fim de justificar a inexistência de universais não funciona, pois a própria semelhança é um universal, dado que ela é partilhada por diversos particulares. Além disso, Russell aponta que ao admitir a existência do universal da semelhança, não há razões para não admitir a existência de outros universais.

O argumento pode ser exposto do seguinte modo (Russell 1912, p. 156):

(P1) Algo é branco se, e somente se, é semelhante a um particular branco;
(P2) Se algo é semelhante a um particular branco, então a semelhança existe em pares de particulares brancos;
(P3) Se a semelhança existe em pares de particulares brancos, então é um universal;
(C) Logo, se algo é semelhante a um particular branco, então é um universal.

Esse argumento pretende mostrar que a relação de semelhança é um universal. O argumento tem uma forma válida, portanto se as premissas forem verdadeiras é impossível que a conclusão seja falsa. Resta-nos saber se as premissas são verdadeiras.

(P1) nos diz que para algo ser branco ele tem de ser semelhante a outro particular branco, ou seja, ser semelhante a outro particular branco é condição necessária e suficiente para ser branco. Isso parece ser verdade: não diríamos em pleno juízo que esta folha de papel é branca, mas não é semelhante à folha anterior no que diz respeito à brancura.

(P2) nos diz que por um particular ser semelhante a um particular branco ele também será semelhante a tantos particulares brancos quanto existirem. Isso se dá justamente por existirem muitos particulares brancos e por “ser branco” ser condição necessária e suficiente para ser semelhante a outro particular branco, como dito por (P1).

Agora examinemos (P3): “Se a semelhança existe em muitos pares de particulares brancos, então é um universal”. Um universal, por definição, é um modo de ser de muitas coisas, ou seja, é uma propriedade partilhada por particulares. Dado que a semelhança existe em mais de uma coisa, ela é partilhada. Logo, é um universal.

Um dos aspectos fundamentais do argumento é que não podemos deixar de postular a existência dos universais, já que a própria semelhança é um universal. E se é legítimo aceitar a existência do universal da semelhança não há razões para não aceitar a existência de outros universais. A razão adicional que motiva o uso dos universais, é que sem ele o nominalista cairá numa regressão infinita.

A regressão infinita ocorre da seguinte forma: o nominalista, para evitar o argumento de Russell, poderia dizer que as semelhanças entre particulares são diferentes umas das outras, ou seja, a semelhança entre os particulares a, b e c, d (S1) é diferente da semelhança entre os particulares a,b e e, f (S2). Porém, ao dizer isso terá de admitir uma semelhança de segunda ordem, já que (S1) é semelhante a (S2) — chamemos essa semelhança de segunda ordem de (S3). Feito isso, terá de admitir outras relações de semelhança de ordens distintas, uma vez que (S3) também é semelhante a (S2) e a (S1). Dado que essas semelhanças sempre serão semelhantes entre si, toda vez que o nominalista quiser explicar uma semelhança terá de postular a existência de outra.

A regressão compromete o nominalismo de semelhança, uma vez que para explicar a semelhança o nominalista introduz uma nova semelhança que carece de explicação tanto quanto a anterior. Por isso resta ao nominalista de semelhança mostrar que o argumento de Russell não funciona, de algum modo, bloqueando a regressão.

2. Quais premissas atacar?

Dadas as premissas do argumento de Russell, quais delas o nominalista terá de negar para defender sua tese? (P1) não só é aceita pelo nominalista de semelhança, como é parte fundamental da sua tese, já que este defende que o que faz um particular ter a propriedade F é ser semelhante a outros particulares. Portanto, o nominalista sustentará (P1).

No entanto, o nominalista não pode aceitar (P2), pois aceitá-la equivale a se comprometer com algo que é partilhado por vários particulares. Negar (P2) é afirmar que algo é semelhante a um particular branco e não existe em pares de particulares brancos. Para defender isso tem de se dizer que a semelhança entre um particular branco A e um particular branco B é diferente da semelhança entre o particular branco C e o particular branco B. Não é a mesma semelhança que existe nos pares de particulares, mas sim outra. Em suma, a semelhança entre dois particulares é ela mesma um particular e para cada particular semelhante haverá o particular da semelhança. Já sabemos que essa tese cairá na regressão infinita de Russell. Portanto, o desafio do nominalista de semelhança é negar (P2).

Repare que o nominalista também não pode aceitar (P3), mas como esta premissa se apóia na premissa anterior, basta refutar (P2) para tornar (P3) uma premissa inútil. Se (P2) é falsa, ela possui uma antecedente verdadeira e uma consequente falsa. A antecedente de (P3) é a consequente de (P2). Logo, se (P2) é falsa, a antecedente de (P3) é falsa. Logo, se a antecedente de (P3) é falsa, (P3) não pode ser utilizada para chegar à conclusão do argumento da regressão. Portanto tudo o que o nominalista precisa fazer para refutar o argumento de Russell é negar (P2).

A seguir apresento duas tentativas de resposta à regressão infinita de Russell. Essas tentativas de resposta não aceitam (P2) e consideram a semelhança como um particular. Defenderei que ambas as respostas falham.

3. Duas respostas nominalistas ao argumento da regressão

A primeira resposta que apresento é a de James Cargile (2003). Cargile defende que uma forma de evitar a regressão de Russell é considerar um dos particulares envolvidos como um paradigma. Seleciona-se um triângulo t como um paradigma da triangularidade, por exemplo. Feito isso, baseamos todas as relações de semelhança em t, ou seja, o triângulo t1 será um triângulo, pois é semelhante a t. Isso reduz o número de relações de semelhança a ponto de evitar a regressão infinita de Russell. Expliquemos melhor.

Primeiramente temos de ver quais são os pressupostos que Cargile assume. Ele assume que o que é chamado de ‘propriedades’ é, na verdade, a semelhança entre os particulares. A semelhança, por sua vez, é tida como uma relação complexa que não é instanciada por múltiplos particulares (2003, p. 549). No entanto, a relação de semelhança não se dá desordenadamente: ela se dá somente entre um paradigma e um particular. Além do mais, ele assume também que há um número finito de particulares. Com esses pressupostos em mente podemos prosseguir.

Dados três particulares (o exemplo original de Cargile é feito com cinco, mas três gera o mesmo efeito) a, b, c em que a é o paradigma, temos as seguintes relações de semelhança:

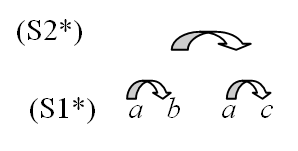
O esquema mostra todas as possíveis relações de semelhança ao tomarmos a como paradigma. (S1*) representa as relações de a com b e a com c, entretanto temos de admitir que essas semelhanças são semelhantes entre si, portanto postulamos (S2*). Não há regresso infinito, já que a regressão parou em (S2*). Como as semelhanças são particulares, não há qualquer entidade partilhada, logo não há universais. Porém, há aí alguns problemas.

O primeiro problema é aceitar os paradigmas. Cargile diz que não é relevante sabermos por que um particular é definido como paradigma, ou seja, por que um triângulo t é o paradigma da triangularidade. Mas como pode não ser relevante se é justamente o ponto central de sua argumentação? Seja o que for um paradigma para Cargile, ele não parece ser um fato bruto ou algo do tipo, mas sim algo convencionado. Cargile pensa que um particular é um paradigma, pois foi escolhido como tal por um agente cognitivo. Sendo algo convencionado, podemos facilmente conceber uma situação em que há a semelhança entre particulares, mas não há quaisquer paradigmas. Um exemplo é o caso em que não havia agentes cognitivos, mas havia pedras semelhantes. Como havia semelhança e não havia agentes cognitivos para determinar que um particular fosse um paradigma, então nessa situação a regressão de ocorreria.

Ainda há outro problema envolvendo os paradigmas de Cargile. Por que temos de aceitar que as relações de semelhança só se dão entre o particular paradigmático e um particular não paradigmático? Não temos. No exemplo dado pelo esquema temos a, b e c, sendo a o paradigma. Suponha que a seja branco, assim b e c são brancos por serem semelhantes a a. Entretanto, se a é semelhante a b e a c, então haverá alguma semelhança entre b e c. Nessa situação temos uma relação de semelhança que se dá entre particulares não paradigmáticos. Sendo assim, haverá outras infinitas relações de semelhança e a regressão infinita de Russell aparece novamente. Daí conclui-se que mesmo aceitando os paradigmas a regressão de Russell ocorre

Outra objeção é a que a exigência de que devemos aceitar apenas um número finito de particulares é irrelevante para a discussão, pois a semelhança tem de dar conta de qualquer particular novo que aparece num dado domínio. Limitar os particulares não parece ser uma boa saída, uma vez que parece ser impossível saber quantos particulares semelhantes aparecerão. A resposta tem de ser dada independentemente de sabermos se o número de particulares é finito ou não. A exigência de Cargile de que os particulares tenham um número finito parece motivada como um meio de impedir o regresso de Russell. De qualquer modo, mesmo se concedermos para fins de argumentação o número finito de particulares, as objeções anteriores ainda têm efeito. A resposta de Cargile, portanto, não funciona. Não temos motivos para admitir paradigmas, uma vez que eles não nos ajudarão em nada para evitar relações entre particulares paradigmáticos e não paradigmáticos.

A segunda resposta é a de Rodriguez-Pereyra (2001) e já é mais sofisticada que a anterior. Ela é baseada inteiramente nos particulares e, por isso, não invoca qualquer entidade ou paradigma. Responder apenas com base nos particulares é uma tarefa dificílima, pois é preciso encontrar um modo de derivar a semelhança somente dos particulares. Veremos que sua resposta requer um custo ontológico muito alto e que ainda assim não parece ser convincente. Antes de tudo, é preciso mencionar que Rodriguez-Pereyra parte de alguns pressupostos diferentes. O primeiro deles é o de que o problema dos universais deve ser entendido como o problema da Muitas para Um ao invés do Um para Muitas. O problema da Muitas para Um é o de explicar como um único particular pode ter diversas propriedades. O segundo pressuposto é o de que as propriedades relevantes para o problema dos universais não são tudo aquilo expresso por predicados, mas somente as chamadas propriedades esparsas ou naturais, que têm relação com poderes causais dos particulares e fazem parte do inventário da física e demais ciências. Outro pressuposto é o de que a relação de semelhança é primitiva no sentido de não poder ser explicada por fatos mais básicos.

Rodriguez-Pereyra defende que solucionar o problema dos universais é nada mais do que fornecer os veridadores das proposições que atribuem propriedades aos particulares. Mas o que são veridadores? Veridador é aquilo que torna uma proposição verdadeira. Por exemplo, qual é o veridador da proposição ‘existe água’? É a água existir de fato. Nas proposições que envolvem propriedades já não é tão claro quais são os veridadores. Um realista diria que na proposição ‘Russell é perturbador’ os veridadores são: Russell existir e instanciar o universal ‘ser perturbador’. Rodriguez-Pereyra, por sua vez, diz que esse não é o caso, já que não há universais. Dado que seu objetivo é explicar as propriedades em termos de relações de semelhança, uma parte fundamental de sua tese é a de fornecer os veridadores das proposições que envolvem semelhança entre particulares.

Daí, temos a seguinte proposição (Rodriguez-Pereyra, 2002):

1. Se os particulares x e y são os veridadores de uma proposição P, então “x existe’ e “y existe’ implica P. (Rodriguez-Pereyra, 2002)

Supondo que os particulares x e y são semelhantes, então:

2. Se os particulares x e y são os veridadores da proposição “x é semelhante a y’, então “x existe’ e “y existe’ implica “x é semelhante a y’.

Como‘x existe’ e ‘y existe’ implica ‘x é semelhante a y’, os particulares x e y são os únicos veridadores da proposição ‘x é semelhante a y’ e, com isso, a mera existência dos particulares x e y é uma condição suficiente para a relação de semelhança entre x e y. Como a semelhança é explicada a partir da mera existência dos particulares, não há qualquer regresso envolvendo a relação de semelhança, que já está explicada.

Essa solução enfrenta algumas objeções difíceis de serem respondidas. Considere um objeto branco. De acordo com o nominalismo de semelhança diríamos que ele é branco em virtude de ser semelhante a outros objetos brancos. Aplicando o raciocínio de Rodriguez-Pereyra, o objeto é semelhante aos outros objetos brancos porque existe. Se o que o torna semelhante aos outros objetos brancos se deve à sua mera existência, o objeto branco é branco simplesmente porque existe. Parece estar faltando aí um pedaço muito grande da explicação. Temos uma intuição contrária a essa explicação de que a mera existência de x e y não implica ou acarreta a semelhança entre x e y. Isso porque pensamos que há pelo menos um mundo possível em os particulares existem, mas não são semelhantes. Nesse mundo, x e y não são veridadores da proposição ‘x é semelhante a y’.

Expliquemos melhor essa intuição. O argumento de Rodriguez-Pereyra é uma espécie de modus ponens:

Se x existe e y existe, então x é semelhante a y.
x existe e y existe.
Logo, x é semelhante a y.

Partindo da suposição de que um argumento é válido quando é impossível que tenha premissas verdadeiras e uma conclusão falsa, basta conceber uma única circunstância ou mundo possível em que as premissas são verdadeiras e a conclusão falsa para demonstrar que o argumento é inválido.

Para responder essa objeção, Rodriguez-Pereyra faz uso do realismo modal e da teoria das contrapartes. Sem entrar em detalhes, o realismo modal sustenta a existência efetiva dos mundos possíveis e a teoria das contrapartes defende que um particular só existe no mundo atual, sendo que nos outros mundos possíveis só existem suas contrapartes, ou seja, particulares maximamente semelhantes, mas distintos dos particulares do mundo atual.

Essas teorias fornecem uma saída para a objeção da seguinte forma: a proposição principal pode ser formulada como uma condicional: se x existe e y existe, então x é semelhante a y. Uma condicional é falsa sempre que sua antecedente for verdadeira e sua conseqüente for falsa. Sendo x e y particulares, de acordo com a tese das contrapartes eles só existem no mundo atual, daí segue-se que não há qualquer mundo possível em que a antecedente da condicional seja verdadeira e a consequente falsa: essas possibilidades apenas ocorrem com as contrapartes de x e y, mas não com x e y. Como é verdade que eles são semelhantes e também não há um mundo possível onde esses particulares não o são, a condicional é verdadeira. Logo, x e y são de fato os veridadores da proposição ‘x é semelhante a y’ e, portanto, ‘x existe’ e ‘y existe’ implica ‘x é semelhante a y’.

Há um meio de rejeitar esse argumento sem colocar em causa a teoria das contrapartes. Rodriguez-Pereyra utiliza uma condicional com antecedente e conseqüente verdadeiras e conclui que a condicional é verdadeira. Portanto podemos inferir a consequente da antecedente por modus ponens. A sua tese está perfeita em termos de lógica clássica, pois uma condicional com a antecedente e a conseqüente verdadeiras é verdadeira. Porém, o argumento de Rodriguez-Pereyra sugere mais do que isso: que a verdade da antecedente ‘x existe e y existe’ é condição suficiente para a verdade da consequente ‘x é semelhante a y’. Mas é aí que a lógica clássica não dá conta de nossas intuições sobre o que é uma condição suficiente. Uma condição suficiente é uma condição que sozinha garante a realização da conseqüente, por exemplo, na condicional “Se estou em Ouro Preto, estou no Brasil”, estar em Ouro Preto é uma condição suficiente para estar no Brasil. Mas há inúmeras condicionais com antecedente e conseqüente verdadeiras nas quais a antecedente não é condição suficiente para a verdade da conseqüente. Dois exemplos são: a) Se os elefantes têm quatro patas, então o sol é feito de gás; b) Se uso óculos, então estou no Brasil.

Nesses dois exemplos a antecedente e a conseqüente estão totalmente desconexas. Não diríamos em pleno juízo que os elefantes terem quatro patas seja suficiente para concluir que o sol é feito de gás. A explicação da conseqüente não se dá por meio da antecedente: parte grande da explicação está faltando. O que isso mostra é que não basta que a condicional de Rodriguez-Pereyra seja verdadeira para concluirmos que a antecedente é uma condição suficiente para a conseqüente. Dizer que dois particulares existem não é suficiente para afirmar que eles são semelhantes. Para responder a essa objeção a teoria precisa explicar por que essa intuição de que uma condição suficiente precisa de algo além dos valores de verdade é equivocada e isso não é feito por Rodriguez-Pereyra.

Rodriguez-Pereyra poderia contra-argumentar defendendo que a antecedente é uma condição suficiente para a consequente, uma vez que a antecedente só pode ser os veridadores da conseqüente – e de fato ele impõe essa restrição na sua tese. O problema dessa resposta é que ela é circular, já que o que se pretende provar são os próprios veridadores da conseqüente, nomeadamente o que faz ser verdade que dois particulares são semelhantes.

Outra crítica que se pode fazer a Rodriguez-Pereyra é acerca do custo ontológico de sua teoria. Por ‘custo ontológico’ entendo a quantidade de entidades e estruturas da realidade que sua teoria postula. A teoria realista, por exemplo, tem um custo ontológico alto, pois tem de assumir a existência de uma nova categoria, nomeadamente, os universais. Já o nominalismo, tem um custo ontológico baixo, pois só postula a existência de particulares. O nominalismo de Rodriguez-Pereyra, apesar de compartilhar a economia do nominalismo, é extremamente pródigo em assumir o realismo modal. Assumindo o realismo modal, compromete-se com a existência efetiva de inúmeros mundos possíveis. Há, por exemplo, um mundo possível, que efetivamente existe, em que a palavra “vírgula” não está escrita neste ensaio. Desde que uma das maiores motivações para se defender o nominalismo tem sido a economia ontológica, parece até um contra-senso adotar tantas estruturas. Esse argumento não invalida a teoria, mas demonstra que o nominalismo perde uma de suas principais motivações.

4.A relevância do argumento de Russell

Até agora só mostramos as falhas em duas tentativas nominalistas de resposta ao argumento de Russell. Apesar da relativa simplicidade de (P2), essa premissa tem resistido a todas as objeções oferecidas na literatura. Dizer que há algo que é semelhante e ao mesmo tempo evitar o regresso infinito é o que o nominalista de semelhança deve fazer para refutar Russell. Mas quais requisitos essa refutação deve satisfazer para funcionar? Antes disso preciso fazer jus a importância e às implicações do argumento de Russell.

O argumento é direcionado ao nominalista de semelhança. No entanto, o mesmo gênero argumentativo pode ser aplicado a qualquer resposta ao problema dos universais, inclusive à própria tese universalista de Russell. Quaisquer teorias que usem relações para explicar as propriedades partilháveis caem em um regresso infinito. O nominalismo de semelhança, apesar de postular somente a existência de particulares, usa de relações de semelhança e é justamente aí que o regresso ocorre. Uma resposta alternativa ao mesmo problema, por exemplo, a resposta realista, também apela para relações. O realista defende que um particular tem uma dada propriedade por instanciar um universal. Ora, há aí a relação entre o particular e o universal, nomeadamente, a relação de instanciação. Mas será essa relação de instanciação a instância de outro universal? Parece que sim, portanto já vislumbramos o regresso. Respostas como a teoria dos tropos e o nominalismo de classes também usam relações e assim caem no mesmo regresso.¹

O argumento de Russell é muito mais importante do que de início colocamos. As dificuldades são impostas a toda e qualquer teoria que use relações. Isso talvez indique que para responder ao argumento de Russell não podemos depender de relações, ou devemos explicá-las de alguma forma que evite que sempre se postule uma nova relação para explicar a anterior.

Alternativas como as de Cargile que se limitam a restringir o domínio dos particulares e apelar para convenções parecem ser superficiais demais para resolver o problema. Penso que uma saída nominalista promissora é a explicação das relações em termos dos próprios particulares ou a partir de fatos brutos. Vimos que é justamente isso que Rodriguez-Pereyra faz. No entanto há muitas razões para rejeitar sua a tese e uma delas é o preço de aceitar todos os seus pressupostos.

Apontar como uma resposta promissora deve ser é demasiado simples. Se é possível dar uma boa resposta em termos não relacionais é um problema em aberto que não tenho resposta . O argumento de Russell, de início restrito somente ao nominalista de semelhança, parece ser um ponto central da discussão acerca dos universais de modo que não é possível simplesmente ignorá-lo.²

Notas

1. Essa extensão do argumento de Russell às outras teorias é detalhada por Armstrong, D.M. (1974). Nesse artigo ele mostra como cada resposta ao problema dos Universais cai no regresso infinito. É importante frisar que na literatura há a variação de nome do regresso, por exemplo, no caso das teorias universalistas o regresso é chamado de “Regresso de Bradley”, porém a espécie de argumento é a mesma.
2. Este artigo é uma modificação do trabalho produzido na disciplina Ontologia ministrada pelo professor Desidério Murcho em 2010, na UFOP. Gostaria de agradecer imensamente as objeções e correções feitas por Matheus Martins Silva, sem as quais o artigo teria muitas mais falhas. Também agradeço as discussões no Seminário Livre de Filosofia da UFOP, no qual sofri algumas objeções que ajudaram a repensar algumas ideias.

Referências