Esta é a versão em linha e gratuita da versão de 2003 do Dicionário Escolar de Filosofia, org. por Aires Almeida (Lisboa: Plátano Editora). Trata-se de um dicionário escolar por ter sobretudo em conta os estudantes do ensino secundário português (alunos entre 15 e 16 anos). Não apenas pela linguagem acessível e directa, mas também pela selecção de conteúdos, este dicionário serve os adolescentes que estudam filosofia pela primeira vez. Uma segunda edição (Lisboa: Plátano Editora, 2009), muitíssimo alargada, foi entretanto publicada.
Dicionário escolar de filosofia
A
a dicto secundum quid ad dictum simpliciter
Expressão latina que significa “da asserção qualificada para a não qualificada”; trata-se de uma falácia informal. Por exemplo: “Todo o deus omnipotente pode fazer tudo; logo, todo o deus pode fazer tudo”. (Desidério Murcho)
a dicto simpliciter ad dictum secundum quid
Expressão latina que significa “da asserção não qualificada para a qualificada”; defende-se por vezes que se trata de uma falácia informal. Por exemplo: “Nenhum cavalo pode voar; logo, nenhum cavalo alado pode voar”. (Desidério Murcho)
a fortiori
Expressão latina que significa “por maioria de razão”. Se todas as opiniões são inúteis, então a fortiori a sua opinião também o é. (Aires Almeida)
a priori e a posteriori
1. Uma distinção entre modos de conhecimento. Conhecemos a priori uma dada proposição quando não recorremos à experiência para a conhecer. Por exemplo, uma pessoa sabe a priori que 23 + 12 = 35 quando faz um cálculo mental, não recorrendo à experiência. Conhecemos a posteriori uma dada proposição quando recorremos à experiência para a conhecer. Por exemplo, uma pessoa sabe a posteriori que o céu é azul quando olha para o céu e vê que é azul. Considera-se, tradicionalmente, que a lógica, a matemática e a filosofia são disciplinas a priori porque têm por objecto problemas cuja solução implica recorrer ao pensamento puro. A história, a física e a economia, por exemplo, são disciplinas a posteriori porque têm por objecto de estudo fenómenos que só podem ser conhecidos através da experiência; por exemplo: para saber em que ano Buzz Aldrin e Neil Armstrong foram à Lua é necessário consultar documentos históricos; para saber qual a taxa de inflação em Portugal em 2003 é necessário consultar dados económicos.
2. Diz-se que um argumento é a priori quando todas as suas premissas são conhecíveis a priori; e diz-se que é a posteriori quando pelo menos uma das suas premissas só pode ser conhecida a posteriori. Não se deve confundir o a priori e a posteriori com o analítico e sintético, nem com necessário e contingente. (Desidério Murcho)
absoluto e relativo
Diz-se que é absoluto o que depende apenas de si próprio, não se submete a quaisquer condições e não tem restrições. Pelo contrário, o que tem uma natureza dependente e não existe por si mesmo é relativo. Por exemplo, dizer que há normas morais absolutas é dizer que essas normas não dependem da época, da sociedade, da opinião das pessoas, etc. Por sua vez, ao dizer que as normas morais são relativas, estamos a afirmar que tais normas dependem de algo que, neste caso, devemos especificar, sendo por isso variáveis. O termo “absoluto” é também utilizado por alguns filósofos como substantivo, para referir uma espécie de ser supremo, espiritual, único e autoconsciente. Um exemplo disso encontra-se na filosofia idealista de Hegel. (Aires Almeida)
abstracção
O processo psicológico que consiste em isolar as características comuns a um dado conjunto de objectos. Também se costuma chamar abstracção ao resultado deste processo. Segundo John Locke, trata-se do processo através do qual adquirimos os conceitos (ver conceito) de homem, árvore, azul, etc. Isso implica que, de entre a variedade de características que cada objecto exemplifica, se retenham apenas as que são comuns a todos os objectos da mesma classe. Assim, o conceito de árvore inclui apenas as características que se podem observar em todas as árvores, sejam elas pinheiros, oliveiras, laranjeiras, etc., e não características particulares como o tamanho, a forma da copa, o textura do tronco, ou a cor e a quantidade de folhas de cada árvore. Para Locke, os animais não são capazes de abstracção; apenas os seres humanos, residindo aí a principal diferença entre ambos. Por sua vez, Berkeley nega a existência da abstracção, pois considera que isso nos leva a conceber coisas que não existem em lado algum, como objectos sem cor, etc. Para este filósofo não há ideias abstractas, defendendo que todas as ideias são concretas. Ver também abstracto e concreto. (Aires Almeida)
abstracto e concreto
Muitas pessoas utilizam o termo “abstracto” para referir algo impreciso, vago, sem conexão com a realidade e sem objectividade. Mas isso é incorrecto. Um termo refere algo abstracto se aquilo que é referido por esse termo não tem existência espaciotemporal, isto é, se não existe num lugar qualquer nem num determinado momento. Por exemplo, a justiça é uma entidade abstracta, pois não tem localização espaciotemporal, não se podendo confundir com os casos concretos de situações justas, que têm localização espaciotemporal. As propriedades são, pois, exemplos típicos de “coisas” abstractas; a propriedade de ser árvore, por exemplo, não se confunde com as próprias árvores. Cada árvore em particular é concreta, dado que existe no espaço e no tempo; mas a própria propriedade de ser árvore é abstracta dado que não existe no espaço nem no tempo. Supostamente, os números e as proposições (ver proposição) também não têm existência espaciotemporal, pelo que são exemplos comuns de entidades abstractas. Por sua vez, diz-se que uma entidade é concreta se tem uma existência espaciotemporal, ou seja, se existe ou existiu numa dada ocasião, num certo sítio. Assim, a árvore que está neste momento à entrada do portão principal da minha escola é uma entidade concreta. Exemplos de entidades concretas são também a dor de dentes que tive hoje à tarde, o suspiro de Pedro ao ver Inês, a ponte Vasco da Gama, a Marisa Cruz, etc. Esta distinção nem sempre é pacífica: os nominalistas, por exemplo, rejeitam a existência de entidades abstractas. (Aires Almeida)
absurdo
1. Em lógica e filosofia, uma afirmação absurda é uma afirmação sem sentido; por outras palavras, sem valor de verdade, como “As ideias verdes dormem furiosamente juntas”. Não basta desconhecer o valor de verdade de uma afirmação para ela ser absurda; é preciso que a afirmação não tenha realmente valor de verdade. Por exemplo, desconhece-se se a afirmação “Há vida microscópica em Marte” é verdadeira, mas a afirmação não é absurda, dado que tem um valor de verdade, apesar de ser desconhecido.
2. Diz-se que a vida ou a existência é absurda quando não tem sentido (ver sentido da vida).
3. Diz-se que uma afirmação é absurda quando é disparatada, ou evidentemente falsa. (Desidério Murcho)
absurdo, redução ao
Ver redução ao absurdo.
acção
Aquilo que é feito intencionalmente por alguém; um acontecimento que resulta directamente da vontade de um agente. Uma pessoa pode causar um acontecimento sem que o tivesse previsto, desejado ou controlado (como quando chuta uma pedra involuntariamente e esta acerta num carro). Neste caso, não se trata de uma acção. Apenas aos acontecimentos causados por alguém de forma intencional (ver intenção), e que têm em vista obter algum resultado, se pode apropriadamente chamar “acções" (como atirar uma pedra a um cão para o afastar do meio da estrada). O movimento corporal não é necessário nem suficiente para assinalar a existência de uma acção: é vulgar alguém fazer a acção de se defender de um cão feroz permanecendo imóvel; e há movimentos quando espirramos sem que isto represente qualquer acção. (António Paulo Costa)
acção afirmativa
Ver discriminação positiva.
acto de fala
J. L. Austin, no seu célebre livro Como Fazer Coisas com Palavras, notou que as línguas humanas contêm frases gramaticalmente assertóricas (ver asserção) que, tipicamente, não são usadas pelos falantes para fazer asserções genuínas. Assim, se eu disser “prometo chegar a horas amanhã”, não estou a descrever uma situação futura, nem a descrever a minha intenção de cumprir a promessa, nem a descrever o acto de fazer a promessa, mas antes a fazer a própria promessa. O mesmo acontece se eu disser “agradeço as tuas palavras" (caso em que estou a agradecer, e não a descrever um agradecimento). Nestes, como em casos semelhantes, não se está a descrever um estado de coisas e, portanto, a elocução respectiva não é candidata a ser classificada como verdadeira ou falsa mas antes como “feliz” ou “infeliz”, consoante se satisfaça ou não certas condições para o sucesso de um acto de fala. Na influente teorização que John Searle fez dos actos de fala, é apresentada uma tipologia das acções praticáveis através do uso da linguagem humana, onde os actos assertivos (aqueles que consistem em descrever, veridicamente ou não, estados de coisas) correspondem apenas a uma das categorias contempladas. Outras categorias são as dos actos compromissivos (como os de prometer ou ameaçar), expressivos (como os de agradecer ou lamentar), directivos (como os de ordenar ou perguntar), declarativos (como os de baptizar ou celebrar um matrimónio) ou declarativo-assertivos (como os de demitir alguém ou declarar aberta uma cerimónia). (Pedro Santos)
acidente
Ver substância e acidente.
ad baculum, argumentum
Expressão latina que significa apelo à força. Ver falácia do apelo à força.
ad consequentiam, argumentum
Expressão latina que significa apelo às consequências. Ver falácia do apelo às consequências.
ad hoc
Expressão latina que significa literalmente “para isso”. Por exemplo, quando se introduz uma hipótese numa teoria em dificuldades para a salvar, diz-se que a hipótese é ad hoc. (Aires Almeida)
ad hominem, argumentum
Expressão latina que significa ataque pessoal. Ver falácia ad hominem.
ad hominem, falácia
Ver falácia ad hominem.
ad ignorantiam, argumentum
Expressão latina que significa apelo à ignorância. Ver falácia do apelo à ignorância.
ad infinitum
Expressão latina que significa literalmente “até ao infinito”.
ad misericordiam, argumentum
Expressão latina que significa apelo à piedade. Ver falácia do apelo à piedade.
ad populum, argumentum
Expressão latina que significa apelo ao povo. Ver falácia do apelo ao povo.
ad verecundiam, argumentum
Expressão latina que significa apelo à autoridade. Ver argumento de autoridade.
afirmação
O mesmo que enunciado.
afirmação da consequente, falácia
Ver falácia da afirmação da consequente.
agente
Aquele que age; a pessoa que faz uma acção. Na tradição filosófica são apontadas pelo menos duas exigências para que se considere que alguém tem a propriedade de ser um agente: a primeira, ser capaz de avaliar e escolher entre as várias opções de acção disponíveis; a segunda, ser capaz de concretizar a escolha que fizer. O problema filosófico da agência consiste em saber se as acções são apenas acontecimentos que envolvem pessoas (ou seres racionais em geral), ou se são acontecimentos causados pelos agentes e, nesse caso, como se dá tal causalidade. Ver causa e efeito e livre-arbítrio. (António Paulo Costa)
agnosticismo
A suspensão da crença em relação à existência de Deus. O agnosticismo forte é a ideia de que nunca poderemos descobrir se Deus existe ou não. (Célia Teixeira)
Agostinho, Santo
Ver Santo Agostinho.
alegoria da caverna
Situação imaginada por Platão no Livro VII de A República (trad. 2001, Gulbenkian) para representar os diferentes tipos de ser que, segundo ele, existem e a condição em que nos encontramos em relação ao seu conhecimento. Vários prisioneiros estão amarrados de pés e mãos numa caverna e só podem olhar para a parede diante deles. Por detrás existe um fogo e entre eles e o fogo passam pessoas transportando vários objectos, cuja sombra se reflecte na parede diante dos prisioneiros, o que os leva a pensar que as sombras são a verdadeira realidade. Só os prisioneiros que são capazes de se libertar (os filósofos), sair da caverna (mundo sensível) e contemplar a realidade e o Sol (mundo inteligível e ideia de Bem) são capazes de compreender como até essa altura viveram num mundo de aparências e ignorância. (Álvaro Nunes)
aletheia
Termo grego que significa “verdade” e de onde deriva o adjectivo “alético”.
alienação
Conceito que se refere a um conjunto de situações em que um ser não se reconhece porque perdeu algo da sua essência. Em Hegel a alienação era uma condição necessária da realização do Absoluto como Espírito que tudo governa. Em Marx o sujeito da alienação é o homem e a alienação é uma degradação física e moral de que urge salvá-lo. Para Marx a alienação fundamental é a económica: o trabalhador é obrigado a vender o seu trabalho para satisfazer necessidades que não são especificamente humanas (comer, beber...). A exploração do trabalho aliena o trabalhador, isto é, desumaniza-o. Na raiz da degradação está a propriedade privada dos meios de produção. Só o comunismo, ao abolir esta situação, poderá salvar o homem. (Luís Rodrigues)
ambiguidade
Uma frase é ambígua quando exprime mais de uma proposição. Por exemplo, a frase “O João está no banco” é ambígua porque tanto pode querer dizer que o João está numa instituição financeira como que o João está sentado num banco. Podemos distinguir dois tipos de ambiguidades: semântica e sintáctica. O exemplo dado é uma ambiguidade semântica. As ambiguidades semânticas resultam da ambiguidade do significado das palavras que ocorrem na frase; no exemplo dado, resulta dos diferentes significados da palavra “banco”. A ambiguidade sintáctica não resulta da ambiguidade do significado das palavras que ocorrem na frase, mas antes do modo como as palavras estão encadeadas. Por exemplo, a frase “O João viu a Maria com os binóculos” pode exprimir duas proposições: que quando o João olhou para a Maria ela estava com binóculos, ou que o João viu a Maria através de binóculos. Algumas ambiguidades são consideradas sintácticas na lógica clássica, mas híbridas ou até semânticas em linguística. É o caso das ambiguidades que dependem da ordem dos quantificadores, como a presente em “Toda a rapariga gosta de um actor" (que pode querer dizer que há um só actor de que todas as raparigas gostam, ou que cada rapariga gosta de um actor diferente). (Desidério Murcho)
âmbito
O âmbito de um operador (por exemplo “alguns” ou “não”) ocorrente numa expressão linguística é a parte da expressão a que ele se aplica. Por exemplo, na frase “Alguns estudantes gostam de filosofia mas detestam estudar”, o quantificador “alguns” tem por âmbito toda a sequência que se lhe segue (está a dizer-se, de alguns estudantes, que gostam de filosofia e, além disso, que detestam estudar); pelo contrário, na frase “Alguns estudantes gostam de filosofia mas o Paulo não” o âmbito do quantificador “alguns” não abrange a oração que começa por “mas”. A noção usa-se tanto no estudo da linguagem corrente como no da lógica. Na lógica, o âmbito dos operadores é assinalado por meio de parêntesis, impedindo a ocorrência de ambiguidades. A linguagem corrente, porém, é rica em ambiguidades de âmbito. Por exemplo, a frase “Todos os estudantes amam uma actriz americana” tem duas interpretações: a de que todos os estudantes amam alguma actriz americana, e a de que há uma actriz americana específica que é amada por todos eles; cada uma destas interpretações corresponde à atribuição de âmbitos diferentes aos quantificadores “todos” e “uma”. Para representar uma ambiguidade de âmbito é necessário analisar o papel dos operadores da linguagem corrente por meio de uma linguagem formal (como a do cálculo de predicados), onde os diferentes significados das frases ambíguas possam distinguir-se claramente. (Pedro Santos)
analítico e sintético
Uma distinção semântica, isto é, baseada no significado dos termos usados. Uma frase é analítica se, e só se, o seu valor de verdade é conhecível unicamente com base no significado dos termos usados. Por exemplo, “Nenhum solteiro é casado” é uma frase analítica porque para saber que é verdadeira basta saber o significado dos termos usados. Uma frase é sintética se, e só se, o seu valor de verdade não é conhecível unicamente com base no significado dos termos usados. Por exemplo, a frase “Nenhum solteiro é feliz” é uma frase sintética porque para saber se é verdadeira ou falsa não basta saber o significado dos termos usados. Kant definia estas noções de forma diferente. Partindo do falso pressuposto de que todas as frases têm uma estrutura sujeito-predicado (como “Sócrates é mortal”), defendeu que uma frase é analítica quando o predicado está “contido” no sujeito. É evidente que por este critério uma frase evidentemente analítica, como “Chove ou não chove” não seria analítica; nem uma frase como “Se Sócrates é grego, é grego”, que é evidentemente analítica, pode contar como analítica segundo a definição de Kant. Não se deve confundir o analítico e sintético com o a priori e a posteriori, nem com necessário e contingente. (Desidério Murcho)
analogia
Fazer uma analogia é estabelecer uma relação de semelhança entre coisas distintas. Por exemplo, quando se diz que tal como qualquer artefacto também a natureza mostra sinais de um criador, estamos a estabelecer uma analogia entre a natureza e os artefactos. Ver argumento por analogia. (Célia Teixeira)
anamnese
O processo que, segundo Platão, nos leva a recordar o que já tínhamos aprendido num estado de existência anterior e que estava como que adormecido na nossa alma. No seu diálogo Ménon, um jovem sem qualquer tipo de instrução consegue mostrar conhecimento de noções geométricas, respondendo apenas às perguntas que lhe são feitas por Sócrates. Platão pretende mostrar com isso que o conhecimento não se adquire neste mundo, mas se alcança por anamnese, salientando assim o seu carácter inato. Ver também ideias inatas. (Aires Almeida)
anamnêsis
Termo grego que significa anamnese ou reminiscência.
antecedente
Numa condicional com a forma “Se P, então Q” chama-se antecedente a P. Por exemplo, a antecedente de “Se Sócrates é um homem, então é mortal” é “Sócrates é um homem”. (Desidério Murcho)
antinomia
Contradição ou paradoxo, aparente ou real, entre dois princípios (ver princípio) ou conclusões (ver conclusão) de raciocínios que parecem igualmente justificados. Em Kant, na Crítica da Razão Pura (trad. 1997, Gulbenkian), as antinomias são contradições em que a razão pura cai necessariamente quando procura o incondicionado nos fenómenos e trata o mundo da experiência (ver experiência) como se tivesse realidade em si. Cada antinomia tem uma tese e uma antítese mutuamente contraditórias, para as quais existem aparentemente razões convincentes. Para além das antinomias da razão pura, existem uma antinomia da razão prática, respeitante ao conceito de soberano bem; uma antinomia do juízo teleológico, respeitante ao mecanismo e à finalidade; e uma antinomia do gosto. (Álvaro Nunes)
antítese
De um modo geral, a oposição entre dois termos ou proposições (ver proposição). Mas a palavra tem também um uso mais específico. Em Kant designa o segundo termo da oposição dialéctica que constitui as antinomias (sendo o primeiro a tese). Na dialéctica de Hegel e no materialismo dialéctico (ver materialismo), da oposição entre tese e antítese resulta uma síntese que supera ambas. (Álvaro Nunes)
apeiron
Termo grego que significa “ilimitado”. O filósofo pré-socrático Anaximandro de Mileto (610–656 a.C.) defendia ser o apeiron a origem do universo, e concebia o apeiron como algo infinito e sem ordem. Ver finitude e infinitude.
apelo à força, falácia do
Ver falácia do apelo à força.
apelo à ignorância, falácia
Ver falácia do apelo à ignorância.
apelo à piedade, falácia do
Ver falácia do apelo à piedade.
apelo ao povo, falácia do
Ver falácia do apelo ao povo.
apelo às consequências, falácia do
Ver falácia do apelo às consequências.
aporia
Um problema ou situação aparentemente sem saída. Diz-se por vezes que os chamados diálogos socráticos de Platão são aporéticos porque neles Sócrates discute problemas para os quais não se consegue encontrar uma solução. (Aires Almeida)
aposta de Pascal
Argumento indirecto a favor da existência de Deus da autoria de Blaise Pascal (1623-62), segundo o qual acreditar em Deus é a melhor aposta. Na ausência de argumentos decisivos a favor ou contra a existência de Deus, o melhor que temos a fazer é decidir se acreditar Nele é ou não uma boa aposta. O melhor resultado possível é Deus existir e termos apostado em acreditar Nele, o que implica a felicidade eterna — o Paraíso. O pior resultado possível é Deus existir e não acreditarmos Nele, o que implica a infelicidade eterna — o Inferno. Logo, o apostador racional deverá apostar em acreditar em Deus. Um dos problemas apontados a este argumento é o facto de partir da ideia de que nada podemos saber acerca de Deus, mas presumir, em contradição com esta ideia, que Deus irá reagir bem a um crente oportunista e mal a um descrente racionalmente íntegro. (Célia Teixeira)
Aquino, S. Tomás de
Ver Tomás de Aquino.
archê
Termo grego que significa origem, princípio ou ponto de partida. A palavra foi introduzida no vocabulário filosófico para referir a substância de que são feitas todas as coisas, ou a partir da qual todas surgiram, e que constituiu o objecto de estudo dos primeiros filósofos pré-socráticos. (Aires Almeida)
aretê
Termo grego que significa “virtude”, “excelência moral” ou “bem humano”. A tradução é problemática porque não existe um termo português que corresponda exactamente ao conceito grego original. Platão usava o termo para falar das virtudes ou bens essenciais para uma vida boa, e distinguia quatro virtudes cardinais: sabedoria (phronêsis), moderação (sôphrosynê), coragem (andreia) e justiça (dikaiosynê). Aristóteles ligava o termo à satisfação da função correcta do ser humano, e portanto à eudemonia ou felicidade. (Desidério Murcho)
Aufklärung
Termo alemão que significa “iluminismo”.
argumento
Um argumento é um conjunto de afirmações de tal modo estruturadas que se pretende que uma delas (a conclusão) seja apoiada pelas outras (as premissas). Por exemplo: “A vida tem de fazer sentido porque Deus existe” é um argumento; a premissa é “Deus existe” e a conclusão é “A vida tem de fazer sentido”. Mas “Ou Deus existe, ou a vida não faz sentido” não é um argumento, dado ser apenas uma afirmação que não está a ser apoiada por outras afirmações. Os argumentos podem ser válidos ou inválidos, mas não podem ser verdadeiros ou falsos. Um argumento é válido quando as suas premissas apoiam a sua conclusão (ver validade e invalidade). Há dois grandes grupos de argumentos: os dedutivos e os não dedutivos (ver dedução e indução).
Não se deve confundir argumentos com explicações (ver explicação científica). Para que um argumento seja bom, a conclusão não pode ser mais plausível do que as premissas. Mas esta exigência não existe numa explicação: a “conclusão” das explicações é quase sempre mais plausível do que as “premissas”. Por exemplo: “Existem estações do ano nas latitudes elevadas porque o eixo da Terra está inclinado, o que provoca, juntamente com o movimento em torno do Sol variações na intensidade com que os raios do Sol chegam à Terra”. Se pensarmos que estas afirmações formam um argumento, cuja conclusão é “Existem estações do ano nas latitudes elevadas”, trata-se de um argumento muitíssimo mau, dado que as premissas são muitíssimo menos evidentes do que a conclusão. Contudo, esta é uma boa explicação da razão pela qual há estações do ano. Assim, num argumento procura-se persuadir alguém da verdade de uma conclusão, ao passo que numa explicação procura-se explicar a alguém a razão pela qual uma dada afirmação é verdadeira. Por isso, num bom argumento parte-se geralmente de premissas mais plausíveis ou evidentes do que a conclusão, o que não acontece numa boa explicação. (Desidério Murcho)
argumento bom
Um argumento válido, dedutivo ou não, que tem premissas verdadeiras e é racionalmente persuasivo. Ver validade e invalidade, argumento forte. (Desidério Murcho)
argumento cosmológico
Tipo de argumento a favor da existência de Deus segundo o qual se tudo na natureza tem uma causa, então tem de existir algo que não dependa de nada que seja a causa de tudo. A conclusão é que esse algo é Deus. A versão mais discutida deste argumento é a de S. Tomás de Aquino. A ideia é a de que dado que as cadeias causais (Ver cadeia causal) não podem regredir infinitamente, tem de existir algo de natureza distinta das coisas naturais que seja a causa de tudo. O maior problema que este argumento enfrenta é o de que, no máximo, apenas mostraria que existe algo responsável pela existência de tudo, mas não que esse algo seja Deus. (Célia Teixeira)
argumento de autoridade
Um argumento baseado no testemunho de outras pessoas, em geral com uma forma lógica "X disse que P; logo, P”, sendo X uma pessoa ou grupo de pessoas e P uma afirmação qualquer. Por exemplo: “Einstein disse que nada pode viajar mais depressa do que a luz; logo, nada pode viajar mais depressa do que a luz”. Não há regras de inferência precisas para argumentos de autoridade, mas ao avaliar um argumento de autoridade devemos ter em mente os seguintes princípios: 1) O especialista invocado (a autoridade) tem de ser um bom especialista da matéria em causa. 2) Os especialistas da matéria em causa (as autoridades) não podem discordar significativamente entre si quanto à afirmação em causa. 3) Só podemos aceitar a conclusão de um argumento de autoridade se não existirem outros argumentos mais fortes ou de força igual a favor da conclusão contrária. 4) Os especialistas da matéria em causa (as autoridades), no seu todo, não podem ter fortes interesses pessoais na afirmação em causa. Precisamente porque em questões filosóficas disputáveis, por definição, os especialistas não concordam entre si, em filosofia os argumentos de autoridade são quase sempre falaciosos. Contudo, a maior parte do conhecimento de cada ser humano baseia-se em argumentos de autoridade, no sentido em que se baseia no testemunho de outras pessoas. Ver falácia. (Desidério Murcho)
Murcho, Desidério, O Lugar da Lógica na Filosofia, Cap. 9 (Lisboa: Plátano, 2003).
argumento dedutivo
Ver dedução.
argumento do desígnio
Argumento por analogia a favor da existência de Deus. A premissa da analogia é a de que os objectos naturais se assemelham a artefactos. Como tal, do mesmo modo que os artefactos têm um criador (um desígnio) responsável pela sua existência, também os objectos da natureza têm de o ter. Dada a complexidade e ordem da natureza, o criador por detrás da natureza tem de possuir uma inteligência divina. A conclusão é que esse criador é Deus. O argumento foi criticado por David Hume nos Diálogos sobre a Religião Natural. Um dos problemas é que a analogia entre artefactos e objectos naturais parece fraca. (Célia Teixeira)
argumento forte
1. Um argumento não dedutivo é forte quando as suas premissas são verdadeiras e a verdade destas torna muito baixa a probabilidade de a conclusão do argumento ser falsa. Por exemplo, o argumento indutivo seguinte é forte: “Todos os corvos observados até hoje são pretos; a cor dos corvos está geneticamente determinada; só poderia alterar-se em condições ambientais diferentes das geralmente escolhidas pelos corvos para viver; logo, todos os corvos são negros”.
2. Quando não sabemos se as premissas de um argumento dedutivo válido são verdadeiras mas achamos que são plausíveis dizemos que o argumento é forte. Por exemplo, muitas pessoas consideram que o seguinte argumento dedutivo válido é forte, pois consideram que a única premissa que não é evidentemente verdadeira (a primeira) é fortemente plausível: “Se os animais sentem dor, é imoral maltratá-los; dado que os animais sentem dor, é imoral maltratá-los”. Aristóteles chamava “dialécticos” a este tipo de argumentos. Note-se que a força de um argumento válido é precisamente igual à plausibilidade da sua premissa menos plausível: é por isso que para argumentar bem a favor de algo é uma boa ideia partir de premissas menos discutíveis do que a sua conclusão. Ver argumento sólido, validade e invalidade, indução. (Desidério Murcho)
argumento fraco
1. Um argumento não dedutivo é fraco quando a verdade das suas premissas não torna elevada a probabilidade de a sua conclusão ser verdadeira. Por exemplo, o seguinte argumento indutivo é fraco: “Todos os corvos que vi até hoje nasceram antes do ano 2100; logo, todos os corvos vão nascer antes do ano 2100”.
2. Quando não sabemos se as premissas de um argumento dedutivo válido são verdadeiras mas achamos que são implausíveis dizemos que o argumento é fraco. Por exemplo, muitas pessoas podem considerar que o seguinte argumento dedutivo válido é fraco porque pensam que a única premissa que não é evidentemente verdadeira (a segunda) é implausível: “Os animais não têm deveres; quem não tem deveres, não tem direitos; logo, os animais não têm direitos”. Por vezes, diz-se também que um argumento dedutivo inválido é fraco. Ver argumento sólido, validade e invalidade, indução. (Desidério Murcho)
argumento indutivo
Ver indução.
argumento ontológico
Argumento a priori a favor da existência de Deus; isto é, um argumento cujas premissas são todas a priori (ver a priori e a posteriori). Uma das versões mais discutidas do argumento é a de S. Anselmo, que parte da definição de Deus como “o ser maior do que o qual nada pode ser pensado”. A ideia é que se Deus não existisse, então não seria o ser maior do que o qual nada pode ser pensado, o que contradiz o ponto de partida; logo, Deus existe. O argumento foi criticado pelo monge Gaunilo, contemporâneo de Anselmo, que argumentou que através do mesmo tipo de argumento se poderia provar a existência de uma ilha perfeita, o que seria absurdo. (Célia Teixeira)
argumento por analogia
Argumento em que uma das premissas consiste numa analogia entre coisas semelhantes em alguns aspectos para se concluir que também são semelhantes em relação a outros aspectos específicos. Por exemplo, se os animais, tal como as pessoas, reagem quando sentem dor, então, por analogia, também eles devem sentir emoções. Um dos argumentos por analogia mais famosos é o argumento do desígnio a favor da existência de Deus. (Célia Teixeira)
argumento sólido
Um argumento válido com premissas verdadeiras. Por exemplo, o argumento “Se Sócrates era francês, era europeu; ele era francês; logo, era europeu” é válido (é um modus ponens) mas não é sólido, porque a segunda premissa não é verdadeira. Aristóteles chamava “demonstrações” aos argumentos sólidos e “argumentos dialécticos” aos argumentos válidos baseados em premissas cuja verdade não é conhecida. Ver validade e invalidade, argumento forte. (Desidério Murcho)
argumento válido
Ver validade e invalidade.
argumentos, tipos de
Há dois tipos gerais de argumentos: os dedutivos e os não dedutivos. Nos argumentos não dedutivos, a validade ou invalidade não depende exclusivamente da forma lógica; por exemplo: “Todos os corvos observados até hoje são pretos; logo, todos os corvos são pretos”. Há dois tipos de argumentos dedutivos: aqueles cuja validade ou invalidade depende exclusivamente da sua forma lógica, como “Se Deus existe, a vida faz sentido; logo, se a vida não faz sentido, Deus não existe”; e aqueles cuja validade ou invalidade é de carácter conceptual, como “O céu é azul; logo, é colorido”. Pode chamar-se aos primeiros “argumentos formais” e “argumentos conceptuais” aos segundos. Os argumentos formais podem dividir-se em dois grupos: os que são estudados pela lógica clássica (como o exemplo dado acima) e os que são estudados pelas lógicas não clássicas (como “A água é necessariamente H2O; logo, a água é possivelmente H2O”). Finalmente, todos estes tipos de argumentos são de carácter proposicional (como “Sócrates e Platão são mortais; logo, Sócrates é mortal”) ou predicativo (como “Sócrates é mortal; logo, há seres mortais”). (Desidério Murcho)
Aristóteles
(384-322 a. C.) Um dos mais influentes filósofos de sempre. Nasceu em Estagira, no norte da Grécia. Foi discípulo de Platão em Atenas e mestre de Alexandre Magno, na Macedónia. Depois da morte de Platão, fundou em Atenas a sua própria escola, a que deu o nome de Liceu. Os seus interesses eram os mais variados. Não houve quase nenhum domínio do conhecimento sobre o qual não tivesse escrito e atribuía uma grande importância à observação da natureza. Ele próprio procedeu a estudos minuciosos nos domínios da física, biologia, psicologia e linguagem. Como é típico nos melhores filósofos, era muito rigoroso na justificação das suas opiniões e meticuloso na ponderação dos argumentos contrários, evitando chegar a conclusões precipitadas. Entre as disciplinas filosóficas que desenvolveu contam-se a lógica, a metafísica, a ética, a filosofia política, e a estética. Pode mesmo dizer-se que foi o fundador da Lógica, começando o seu estudo praticamente do nada. Se bem que limitada e com várias deficiências, a teoria lógica aristotélica foi o resultado de um trabalho notável de inteligência, de tal modo que, no essencial, se manteve incontestada e estudada até ao final do séc. XIX. Aristóteles procurou determinar as formas válidas de inferência, isto é, as inferências cuja forma nos impede de chegar a uma conclusão falsa a partir de premissas verdadeiras (ver premissa). E estabeleceu um conjunto de regras para identificar as boas e evitar as más inferências (ver lógica aristotélica). Organon é o nome dado ao conjunto das suas obras de lógica. Na Metafísica, uma das suas obras mais marcantes (assim chamada apenas porque foi publicada a seguir à Física), Aristóteles descreve esta disciplina como o estudo do “ser enquanto ser”, isto é, o estudo do ser em geral, independentemente do modo particular como as coisas são. Muitos dos conceitos metafísicos ainda hoje utilizados foram introduzidos por si. Em Ética a Nicómaco (assim chamada por ter sido dedicada a seu filho Nicómaco), Aristóteles argumenta, entre outras coisas, a favor da ideia de que as virtudes morais, como a generosidade e a honestidade, não são inatas. Só o hábito de evitar excessos de qualquer tipo nos pode tornar pessoas virtuosas. Por isso, a virtude adquire-se com a prática. Sobre filosofia política escreveu a Política e sobre estética a Poética, entre outros livros. (Aires Almeida)
Aristóteles, Categorias (Lisboa: Instituto Piaget, 2000)
Aristóteles, Da Alma (Lisboa: Edições 70, 2001)
Aristóteles, Poética (Lisboa: INCM, 1994)
Aristóteles, Retórica (Lisboa: INCM, 1998)
Aristóteles, Tratado da Política (Mem Martins: Europa-América, 1977)
Kenny, Anthony, História Concisa da Filosofia Ocidental, capítulo 4 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, capítulo 2 (Lisboa: Presença, 1989)
Ross, David, Aristóteles (Lisboa: D. Quixote, 1987)
arte, filosofia da
Ver filosofia da arte.
artefacto
Os objectos que são construídos ou manufacturados, como martelos, livros, filmes, casas, esculturas, etc. Distinguem-se das coisas naturais, como as ondas do mar, as nuvens e as árvores. Em geral os filósofos da arte consideram que as obras de arte são artefactos. Daí que um belo pôr-do-sol não seja uma obra de arte. Contudo, visto que os movimentos que constituem uma peça de bailado, ou os sons que um cantor produz são frequentemente considerados arte, o termo “artefacto” tem sido interpretado de modo a incluir também esse tipo de acontecimentos. Ainda assim, podem encontrar-se outros casos na arte contemporânea que desafiam a ideia de que uma obra de arte tem que ser um artefacto. (Aires Almeida)
asserção
Acto linguístico que consiste na produção de uma frase declarativa com valor assertórico, ou seja, um acto linguístico através do qual o seu autor se compromete com a veracidade da proposição expressa. Muitas vezes uma frase declarativa parece ter valor assertórico mas não é susceptível de ser classificada como verdadeira ou como falsa, não fazendo qualquer asserção (por exemplo, “Prometo chegar a horas amanhã”). Ver também pragmática. (Pedro Santos)
ataraxia
Termo grego que significa “imperturbabilidade da alma” ou “tranquilidade interior”. Os epicuristas e estóicos consideravam-na o mais perfeito estado de felicidade. Ver epicurismo e estoicismo. (Aires Almeida)
ateísmo
Em sentido fraco, descrença na existência de uma entidade sobrenatural particular (o Deus teísta), omnipotente, omnisciente, perfeitamente boa, criadora do mundo, mas distinta deste e dotada de auto-existência (não existe por causa de outra coisa). Em sentido forte, é a crença na inexistência do divino em geral. A distinção é importante, pois muitas pessoas religiosas não são teístas (ver teísmo) nem ateístas, ou seja, acreditam em entidades sobrenaturais que não correspondem à ideia do Deus teísta, que é basicamente a ideia de Deus presente nas grandes tradições religiosas do Ocidente: judaísmo, cristianismo e islamismo. Os argumentos ateístas dividem-se em a) argumentos que visam demonstrar a inexistência de Deus e b) contra-argumentos aos principais argumentos teístas a favor da existência de Deus. Apesar de a popularidade da crença teísta sugerir o contrário, o ateísta considera que não está obrigado a apresentar argumentos do primeiro tipo — embora alguns filósofos ateístas procurem fazê-lo —, dado que o ónus da prova recai, neste caso, sobre a afirmação e não sobre a negação: cabe a quem propõe uma dada crença fundamentá-la racionalmente. Alguns dos principais argumentos ateístas do primeiro tipo são o chamado “problema do mal”, o problema da incompatibilidade dos atributos divinos, o problema da diversidade de religiões e o problema da descrença. O primeiro é um argumento que procura negar a existência do Deus teísta a partir da incompatibilidade entre a existência de mal ou sofrimento intenso no mundo e o atributo da perfeita bondade divina; o segundo tem diferentes versões, a mais conhecida das quais foi apresentada por Michael Martin (n. 1932), e consiste em mostrar que a incorporeidade é incompatível com a omnisciência: um ser incorpóreo não poderia ter conhecimento por contacto nem conhecimento performativo, mas apenas proposicional, logo, haveria seres corpóreos não omniscientes que saberiam coisas que Deus não sabe; o terceiro procura recusar a crença teísta com base na existência de múltiplas pretensões absolutas à verdade religiosa, sem que tenhamos qualquer razão forte para escolher uma delas em particular; o quarto consiste em mostrar que os atributos do Deus teísta são incompatíveis com a existência de descrentes: um Deus infinitamente bom e poderoso, que nos ama infinitamente, não deixaria de dar provas inequívocas da sua existência e impedir-nos-ia de acreditar que não existe. A partir daqui a crença teísta tem duas linhas de sustentação: 1) argumentos a favor das afirmações teístas fundamentais e 2) argumentos para proporcionar “imunidade epistémica" às afirmações teístas. Um destes últimos argumentos consiste em negar que as crenças deste tipo (a fé, as crenças com conteúdo religioso) possam ser avaliadas racionalmente como as outras crenças (ver fideísmo). Outra defesa consiste em afirmar que a crença teísta é “apropriadamente básica" (Alvin Plantinga), ou seja, é o tipo de crença que o agente não sabe justificar adequadamente mas que é racionalmente aceitável. (Vítor Guerreiro)
atitude estética
Disposição para nos relacionarmos com as obras de arte (e também com certos objectos ou aspectos da natureza) de forma meramente contemplativa e desinteressada. Esta caracterização sugerida por Kant significa que a apreciação das obras de arte não tem qualquer intuito prático, sendo isso que distingue a experiência estética de qualquer outro tipo de experiência. A atitude estética é, assim, a forma peculiar como encaramos a arte e as coisas belas, pelo que não deve ser confundida com outras atitudes como a religiosa, prática, moral, etc. Há, contudo, filósofos que rejeitam a existência de uma atitude peculiar que caracterize o modo como encaramos a arte em geral. O filósofo americano George Dickie (n. 1926) é autor de um ensaio intitulado O Mito da Atitude Estética (1964), onde argumenta que o desinteresse diz-nos mais acerca dos motivos de quem observa uma obra de arte do que acerca do modo como, em geral, nos relacionarmos com ela. (Aires Almeida)
autonomia e heteronomia
Um agente é autónomo quando as suas acções são autodeterminadas. Segundo Kant é a característica de uma vontade que cumpre o dever, não sendo condicionada por qualquer inclinação sensível (interesses, temores, desejos). A vontade autónoma considera imperativo categórico ou incondicional a obediência à lei moral. Esta exige que ao cumprir o dever apenas sejamos influenciados pela intenção de o cumprir (cumprir o dever pelo dever). À autonomia opõe-se a heteronomia. A vontade heterónoma pode cumprir o dever mas com a intenção, por exemplo, de agradar, de obter recompensas ou de evitar castigos (não cumpre o dever pelo dever). A vontade autónoma “dá a lei a si mesma”. Dá a si mesma a forma como cumpre o dever e encontra no cumprimento da lei moral a razão suficiente das suas decisões. Autodetermina-se. Liberta de qualquer influência das inclinações sensíveis, a vontade autónoma é a vontade de um sujeito que toma decisões enquanto ser racional e se submete unicamente à lei da sua razão. Deus, os interesses, a sociedade podem ser fonte de normas morais concretas mas não da lei moral, lei puramente formal que não nos diz o que devemos fazer mas de que forma devemos cumprir o dever. É a autonomia da vontade que torna a vontade boa. “Vontade autónoma” e “vontade boa” são termos equivalentes. (Luís Rodrigues)
auto-refutação
Uma afirmação é auto-refutante se o próprio facto de ser produzida implica a falsidade do que está a ser afirmado. Quem produzir afirmações como “Eu não estou aqui”, “Paulo Portas é ambicioso mas eu não acredito nisso” e, provavelmente, “O significado de uma frase ou de um texto escapa-se-nos infindavelmente” está a auto-refutar-se. (Pedro Santos)
axiologia
Teoria dos valores. A axiologia é o ramo da filosofia que estuda a natureza dos valores. Alguns filósofos consideram que o problema central da axiologia é a justificação dos juízos práticos em geral, confundindo-se em grande parte com a filosofia da acção e, mais recentemente, com a teoria da decisão. Outros acham que se trata da justificação dos juízos morais em particular. (Aires Almeida)
axioma
Em lógica e matemática, um axioma é uma proposição que não se demonstra, mas que serve de base para se demonstrar outras proposições, a que se chama “teoremas”. Os teoremas são demonstrados partindo dos axiomas e usando regras de inferência. Por exemplo, partindo dos axiomas (P ∧ Q) → P e P → (P ∨ Q) podemos derivar o teorema (P ∧ Q) → (P ∨ Q), com base na regra conhecida pelo nome de “silogismo hipotético”. Figurativamente, chama-se “axioma”, no discurso corrente, a qualquer afirmação dada como evidente e com base na qual se podem fazer outras afirmações. Contudo, não se deve pensar que os axiomas, quer em sentido figurado, quer no sentido rigoroso da lógica e matemática, são Verdades monolíticas arbitrárias que não podem ser colocadas em causa nem discutidas. Um bom axioma não pode ser arbitrário e tem de resistir à discussão crítica: tem de ser realmente indisputável, ou pelo menos muitíssimo plausível. Caso contrário, tudo o que se disser com base nesse “axioma” será tão implausível, ou mais, do que o próprio “axioma”. (Desidério Murcho)
B
Bedeutung
Termo alemão que significa “referência” e se opõe a Sinn (sentido). Frege introduziu esta distinção para separar o que um termo refere da maneira como o termo refere: os termos “Mestre de Platão” e “O filósofo que bebeu a cicuta” referem a mesma coisa (Sócrates), mas referem essa coisa de maneiras diferentes: têm diferentes sentidos. (Desidério Murcho)
beleza
Harmonia, proporção, equilíbrio, graciosidade, e elegância são alguns exemplos de propriedades estéticas (ver propriedade), mas a beleza é a propriedade estética mais central, para a qual contribuem propriedades como as anteriores. Ao contrário do que por vezes se pensa, não foram muitos os filósofos que procuraram identificar as características que algo deve ter para se poder chamar “belo”. Entre esses filósofos contam-se Platão, Tomás de Aquino, Hume, Kant, Monroe Beardsley (1915-85) e Frank Sibley (1923–96). Apesar de cada um deles enfatizar mais uma ou outra característica, todos acabam por convergir na ideia de que a beleza é algo 1) que tem um valor positivo; 2) que nos agrada ou proporciona prazer; 3) que é inspirador e motivador; 4) cuja apreciação depende da percepção ou de alguma forma de contacto com o que é objecto apreciação e 5) cuja apreciação é independente de qualquer interesse teórico ou prático, exprimindo-se através de um de juízo próprio, o juízo estético. Diferentes problemas foram discutidos também por outros filósofos. Trata-se de problemas de carácter metafísico (ver metafísica), epistemológico (ver epistemologia) e ético (ver ética). A discussão metafísica acerca da natureza da beleza inclui problemas com o seguinte: a beleza tem uma natureza subjectiva (ver subjectivismo) ou objectiva (ver objectivismo)? Kant e Hume pensam que a beleza tem uma natureza subjectiva, dado que consiste, segundo eles, no sentimento do sujeito, ao passo que Platão e Beardsley defendem que tem uma natureza objectiva, dado que dizem residir em certas propriedades exemplificadas pelos objectos. Se, por sua vez, perguntarmos “Como sabemos o que é belo?”, estaremos no domínio da epistemologia da beleza. À pergunta anterior há quem, como Hume e Kant, responda que descobrimos a beleza através de uma faculdade especial, a faculdade do gosto; quem, como Clive Bell (1881–1964), defenda que é a através de uma espécie de intuição e quem, como Schopenhauer, defenda que é através do intelecto. Há ainda a questão de saber se a apreciação da beleza tem alguma finalidade ou valor ético. Platão defende que a beleza conduz ao bem, acabando por se identificar com ele, ao passo que os estetas decadentistas (ver decadentismo) defendem que a beleza e a moral são coisas completamente independentes. Há ainda a questão ontológica sobre se há diferentes tipos de beleza e quais. (Aires Almeida)
bem
Em termos algo imprecisos, o bem é aquilo que tem valor em si — valor intrínseco — e é desejável por si. Nesse sentido, o bem seria a finalidade última das nossas acções. Mas que finalidade é essa a que chamamos “bem"? A resposta de Aristóteles e seus contemporâneos foi que essa finalidade é a eudemonia, que costumamos traduzir por felicidade, mas que inclui um vida virtuosa e bem-sucedida. Uma resposta alternativa, dada pelos utilitaristas, é que o bem é o prazer e a ausência de dor e sofrimento. Mas há quem não considere estas respostas satisfatórias. Por um lado, pensamos que há meios que nem mesmo a procura da felicidade justifica, caso em que há outras coisas tão ou mais valiosas que a felicidade. Por outro lado, uma vida isenta de dor e recheada dos prazeres que se queira, mas inautêntica (por exemplo, se estivermos sob o efeito de uma espécie de droga), também não é uma vida desejável. Uma maneira de evitar este tipo de objecções, é fazer como G. E. Moore, declarando que o termo “bem” não é analisável e que o bem é conhecido por intuição: não o sabemos definir mas reconhecemo-lo quando o encontramos. Isto, contudo, ainda não é completamente satisfatório, pois acabamos por identificar o bem com coisas diferentes. Assim, continua em aberto a discussão — que se desenvolve no âmbito da ética e da teoria do valor — sobre o que significa o termo “bem”; sobre que coisas são boas e como sabemos isso; sobre qual é o maior bem; e sobre que tipos de bem existem. (Aires Almeida)
Berkeley, George (1685–1753)
Filósofo e bispo irlandês. Berkeley defende uma forma extrema de idealismo, segundo a qual “esse est percipi" (ser é ser percepcionado). Por outras palavras, uma árvore, por exemplo, não tem qualquer existência material independente da nossa percepção da sua cor, textura, solidez, etc. Apesar disso, a árvore não é menos real nem a sua existência menos objectiva, dado que a nossa percepção dela é involuntária. Assim, o idealismo de Berkeley, apesar de radical, é objectivista, ainda que seja comum dizer-se, erradamente, que ele é um idealista subjectivista (ver objectivo e subjectivo). O idealismo de Berkeley tem tendência para parecer uma ilustração das ideias disparatadas típicas de filósofos ociosos; mas esta impressão falsa só subsiste quando não se compreendem os problemas a que Berkeley estava a dar resposta. No contexto filosófico da época, o dualismo cartesiano (ver Descartes) introduzia um fosso entre as ideias (ou a mente) e o mundo físico; e Berkeley considerava que a resposta de Locke era insatisfatória, tendo como consequência o ateísmo e o cepticismo. Ao eliminar a materialidade do mundo, Berkeley procura eliminar o fosso entre a mente e o mundo. O valor de Berkeley não reside tanto na conclusão a que chegou e que nunca foi muito levada a sério, mas no vigor e brilho da sua defesa, clara e articulada, honesta e acessível ao leitor comum. O Tratado do Conhecimento Humano (1710) é uma defesa brilhante e sintética das suas ideias; os Três Diálogos entre Hilas e Filonous (1713), menos sintéticos, são uma exposição mais literária e popular das ideias da obra anterior. (Desidério Murcho)
Berkeley, George, Tratado do Conhecimento Humano e Três Diálogos (Lisboa: INCM, 2000).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 14 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 6 (Lisboa, Presença, 1989).
bicondicional (↔)
Uma afirmação com a forma “P se, e só se, Q”, como “Uma coisa é arte se, e só se, for bela”. No discurso corrente omite-se muitas vezes um dos ses: “Ofereço-te um livro se passares de ano” quer em geral dizer “se, e só se, passares de ano”. Uma bicondicional é uma conjunção de duas condicionais: “P se, e só se, Q” é o mesmo que “Se P, então Q, e se Q, então P" (ver condicional). Uma bicondicional só é verdadeira quando ambas as proposições têm o mesmo valor de verdade e por isso chama-se-lhe também “equivalência”. As definições mais rigorosas usam bicondicionais para conectar o que se está a definir com o que o define. (Desidério Murcho)
bioética
Ramo da ética aplicada relativo às questões morais suscitadas pela medicina e pela biologia. Na bioética discute-se, por exemplo, a moralidade do aborto, da eutanásia, das experiências com animais, da clonagem, da manipulação genética ou dos transplantes de órgãos. A discussão destas questões exige não só um conhecimento médico e científico especializado, mas também um domínio das teorias éticas normativas que os filósofos propõem. Ver normativo e descritivo. (Pedro Galvão)
C
cadeia causal
Sucessão de acontecimentos relacionados entre si como causa e efeito (Ver causa e efeito). Por exemplo, o acontecimento de o João ter partido a janela da escola com a bola, tem a seguinte cadeia causal: o atirar da bola pelo João como causa e o partir da janela como efeito. Mas a cadeia causal não pára aqui. Por exemplo, o João pode ter atirado a bola contra a janela por se sentir frustrado com a nota de filosofia. E o que causou a sua frustração foi não ter estudado o suficiente, e assim por diante. As cadeias causais podem mesmo regredir infinitamente. (Célia Teixeira)
cálculo de predicados
O tipo de linguagem que contém o cálculo proposicional e ainda símbolos predicativos, quantificadores (ver quantificador), variáveis e constantes individuais (as traduções formais de nomes de indivíduos), bem como regras de inferência (e, eventualmente, axiomas) apropriadas para eles. Ao contrário do cálculo proposicional, o cálculo de predicados permite analisar a estrutura predicativa das proposições e assim representar relações lógicas como as existentes entre 1) “Todos os seres vivos são mortais” e 2) “O Rui é um ser vivo imortal" (contradição) e entre 1 e 3) “Não é verdadeiro que alguns seres vivos não sejam mortais" (equivalência). As fórmulas bem formadas desta linguagem predicativa são usadas em derivações, que são versões formais de argumentos formulados em linguagem corrente (ver cálculo lógico). Desde o início do séc. XX, o cálculo de predicados tem ocupado o lugar da lógica aristotélica como o instrumento de análise lógica por excelência, e é geralmente considerado a linguagem formal na qual a esmagadora maioria dos padrões do raciocínio válido é representável rigorosamente. É ainda utilizado como meio (ou pelo menos como inspiração) para o estudo sistemático de muitas subtilezas sintácticas e semânticas da linguagem corrente. Ver também lógica, lógica clássica, lógica formal. (Pedro Santos)
cálculo lógico
Um sistema formal que permite derivar (ver derivação) conclusões a partir de premissas por meio de regras de inferência. Um cálculo lógico contém uma linguagem bem definida nos seus símbolos básicos e nas regras de construção de fórmulas, além de uma especificação das regras de inferência (e, nos casos de existirem, dos axiomas) admitidas. O conjunto destas especificações determina quais as derivações admitidas no sistema (ver sintaxe). O cálculo proposicional e o cálculo de predicados são exemplos canónicos de sistemas deste tipo. Assim caracterizados, os cálculos lógicos são apenas linguagens formais cujas fórmulas são manipuláveis através de regras, de modo a obterem-se outras fórmulas; mas é evidente que eles serviriam de muito pouco se as suas derivações não fossem modelos dos nossos raciocínios válidos. Assim, para além destas especificações sintácticas, um cálculo lógico pode ser interpretado (ver interpretação, semântica), isto é, podem ser atribuídos significados aos seus símbolos básicos e fórmulas, e as suas derivações podem ser avaliadas como válidas ou inválidas. Idealmente, todas as derivações admitidas num cálculo lógico são válidas e todos os argumentos válidos representáveis na sua linguagem correspondem a derivações nele admitidas. O cálculo proposicional e o cálculo de predicados têm esta característica, a que se chama “completude”. Ver também lógica, lógica clássica.
cálculo proposicional
O tipo de linguagem onde são representadas as relações logicamente relevantes entre proposições (ou entre as frases que exprimem essas proposições): negação, conjunção, disjunção, condicional, bicondicional. Contém letras do alfabeto, como P, Q e R (cada uma delas representando uma proposição), e constantes lógicas (ver conectiva), que são definidas como operadores verofuncionais que actuam sobre as letras proposicionais para construir fórmulas (correspondentes à frases da linguagem corrente). Contém ainda regras de inferência (e, eventualmente, axiomas), o que permite que as fórmulas bem formadas da linguagem sejam usadas em derivações (versões formais de argumentos formulados em linguagem corrente — ver cálculo lógico). No cálculo proposicional são representáveis inferências como “Se o Rui é um ser vivo, então é mortal; o Rui é um ser vivo; logo, é mortal”; mas não são representáveis inferências como “Todos os seres vivos são mortais; o Rui é um ser vivo; logo, o Rui é mortal”. Isto deve-se ao facto de, ao contrário do que acontece com o cálculo de predicados, no cálculo proposicional não ser possível representar a estrutura predicativa das proposições (de modo que a segunda inferência seria nele desinformativamente representada apenas como P; Q; logo, R, o que não daria conta da sua validade). Ver também lógica, lógica clássica, lógica formal. (Pedro Santos)
caprichoso, pensamento
Ver pensamento caprichoso.
caracterização
Caracteriza-se algo quando se apresentam algumas das suas propriedades ou características importantes. Por exemplo, pode-se caracterizar o álcool como um líquido transparente que usamos para desinfectar feridas, que é muito inflamável e volátil, etc. Em suma, escolhemos um conjunto de propriedades que reputamos importantes ou típicas e apresentamos essas propriedades. As caracterizações distinguem-se das definições explícitas (ver definição explícita) por não apresentarem obrigatoriamente condições necessárias nem suficientes (ver condição necessária e condição suficiente). As caracterizações são auxiliares preciosos para a compreensão e podem ser usadas para complementar definições que, apesar de mais correctas, são muitas vezes menos informativas. (Desidério Murcho)
Murcho, Desidério, “Definição de “Definição"" in A Natureza da Filosofia e o seu Ensino (Lisboa: Plátano, 2002).
carácter
Ter um certo carácter é equivalente a ser um certo tipo de pessoa. A avaliação moral do carácter de uma pessoa faz-se a partir dos traços de carácter que exibe. Um traço de carácter é uma disposição estável para agir e que se manifesta no comportamento correspondente. É assim uma disposição comportamental. Mas é também uma disposição para distinguir os aspectos moralmente relevantes dos casos e dar-lhes um certo peso nas nossas deliberações. É também, por isso, uma disposição cognitiva. Por exemplo, a compaixão é um traço de carácter que distingue as necessidades dos outros como um aspecto moralmente relevante a ter em conta. Um traço de carácter envolve ainda uma disposição para sentir, e é, nessa medida, uma disposição emocional. Isto quer dizer que uma pessoa de carácter compassivo sentirá, obviamente, compaixão. Há dois tipos de traços de carácter: os desejáveis e os indesejáveis. Os primeiros são virtudes; os segundos são vícios. Para a ética das virtudes, na qual a noção de carácter tem um papel fundamental, devemos desenvolver as primeiros e evitar os segundos. (Faustino Vaz)
Carnap, Rudolf (1891–1970)
Filósofo americano nascido na Alemanha. Positivista lógico, foi um dos filósofos mais importante do séc. XX. Carnap foi aluno de Frege tendo sido profundamente influenciado por este, assim como por Russell e Wittgenstein. Leccionou nas universidades de Viena e Praga, mudando-se para os EUA em 1935. As suas principais contribuições são em semântica formal (Meaning and Necessity, 1937), filosofia da ciência, lógica e teoria da probabilidade (The Logical Foundations of Probability, 1950). Numa das suas primeiras obras (Der logische Aufbau der Welt, 1928), defendeu a redução de todo o conhecimento humano aos dados dos sentidos ligados pela relação de recordação de semelhança. Posteriormente, reconsidera esta posição abrindo uma excepção para o caso da física. A sua posição anti-metafísica segundo a qual as afirmações metafísicas não têm significado por não serem empiricamente verificáveis (ver verificacionismo) tornou-se emblemática do positivismo lógico. Carnap defende ainda a redução das verdades da matemática e da lógica à linguagem, considerando-as assim de meras verdades por convenção. Pensava também que o único método de fazer filosofia é através da análise lógica da linguagem. Defendia a unidade da ciência e a centralidade da noção de confirmação para o método científico. (Célia Teixeira)
cartesiano
Que se refere a Descartes.
catarse
O processo psicológico de libertação de maus sentimentos e de purificação dos bons. Segundo Aristóteles, a arte proporciona-nos essa oportunidade, contribuindo para nos tornar melhores. (Aires Almeida)
categorias
O termo foi usado pela primeira vez por Aristóteles para designar as classes mais gerais de seres (ver ser) ou os predicados (ver predicado) que podem ser afirmados de um sujeito. Para Aristóteles, as categorias são dez: substância, quantidade, qualidade, relação, lugar, tempo, posição, posse, acção e paixão. A palavra é mais tarde retomada por Kant para designar doze conceitos (ver conceitos) puros do entendimento, formas a priori de conhecimento, que agrupa sob quatro grandes classes: quantidade, qualidade, relação e modalidade. (Álvaro Nunes)
categórica, proposição
Ver proposição categórica.
categórico, imperativo
Ver imperativo categórico.
causa e efeito
Os dois termos de uma relação causal. Chama-se “causa” ao que provoca algo; e “efeito” ao que é provocado. Do ponto de vista temporal, é comum pensar-se que a causa é anterior ao efeito, mas alguns fenómenos estudados na física quântica parecem desmentir esta crença. O modo como se estabelece a relação entre a causa e o efeito tem sido objecto de amplo debate entre os filósofos, especialmente a partir de Hume, no séc. XVIII. Acontecimentos, mudanças e estados (físicos ou mentais) exemplificam aquilo que pode estar causalmente relacionado: quando afirmamos “o calor dilata os metais”, estamos a enunciar uma relação causal em que o aumento da temperatura é a causa e a dilatação dos metais é o efeito. Numa cadeia causal, a causa próxima é aquela que antecede um dado efeito sem a mediação de qualquer outro acontecimento ou estado; pelo contrário, quaisquer outras causas existentes nessa cadeia são causas remotas. Se existir, a Causa Primeira é aquela que causou todas as cadeias causais sem que ela própria tivesse sido causada. Alguns teístas (ver teísmo) identificam-na com Deus. Ver argumento cosmológico. (António Paulo Costa)
causalidade
Ver causa e efeito, relação causal e cadeia causal.
caverna, alegoria da
Ver alegoria da caverna.
cepticismo
A perspectiva que nega total ou parcialmente a possibilidade do conhecimento. De acordo com o céptico, se bem procurarmos, encontramos sempre boas razões para duvidar mesmo das nossas crenças mais fortes. Há dois grupos de argumentos cépticos: o primeiro baseia-se nas diferenças de opinião, mesmo entre as pessoas mais conhecedoras; o segundo, baseia-se nas ilusões perceptivas. Há diferentes tipos de cepticismo. Uma forma radical de cepticismo é geralmente atribuída a Pirro de Élis (c.360 a. C.-c.270 a. C.), para quem devíamos suspender o nosso juízo em relação a todas as coisas. A resposta habitual a este tipo de cepticismo é procurar mostrar que é auto-refutante (ver auto-refutação), pois se podemos afirmar que nada sabemos é porque já sabemos precisamente isso. Também Descartes procurou responder aos argumentos cépticos, mostrando que há pelo menos uma coisa que resiste à dúvida mais insistente: que existimos. Além do cepticismo radical há outros tipos de cepticismo que limitam o seu âmbito apenas a certas áreas. Este tipo de cepticismo parcial pode aplicar-se a aspectos metodológicos: empiristas, como Hume, são cépticos em relação ao conhecimento a priori do mundo (ver a priori e a posteriori), enquanto que alguns racionalistas duvidam do conhecimento empírico. Mas também se pode dirigir apenas a determinado tipo de entidades: o conhecimento de outras mentes, a existência de Deus, o conhecimento do futuro, a indução (ver problema da indução), o conhecimento de verdades éticas, o conhecimento do mundo exterior, etc. Sexto Empírico (c. 150–c.225) e Michel de Montaigne (1533–92) são dois dos mais destacados defensores do cepticismo. (Aires Almeida)
certeza
Grau máximo de convicção acerca da verdade de uma certa proposição. Quando afirmamos “Tenho a certeza absoluta de que P!”, estamos a exprimir a nossa completa convicção de que P é verdade. Mas podemos perfeitamente estar enganados. A certeza não implica a verdade, ao contrário do conhecimento. (António Paulo Costa e Desidério Murcho)
Chomsky, Noam (n. 1928)
Linguista norte-americano e inspirador do movimento generativista em linguística. As suas ideias revolucionaram a disciplina, redefinindo-a no seu objecto e na sua metodologia. A linguística passou a ser vista como a disciplina que estuda a competência gramatical dos falantes e o modo como ela é obtida; sendo acerca do conhecimento que cada falante tem da sua língua, pretende descrever esse conhecimento e não tem, portanto, carácter prescritivo. A visão chomskiana do papel da linguística é inseparável da sua tese inatista de que as características essenciais do conhecimento linguístico humano são determinadas geneticamente; tal como uma cria de pardal está geneticamente programada para um dia vir a voar, também os seres humanos estão geneticamente equipados com a capacidade de compreender e produzir estruturas linguísticas com certas características. Chomsky chamou “gramática universal” ao conjunto de princípios abstractos que definem o potencial linguístico de um falante humano. Os princípios abstractos da gramática universal concretizar-se-ão, à medida que cada criança vai aprendendo a falar uma dada língua, no seu conhecimento gramatical dessa língua específica. Dois argumentos importantes a favor desta visão mentalista e racionalista acerca do conhecimento linguístico são o da pobreza dos estímulos exteriores (segundo o qual a informação linguística que uma criança obtém a partir de estímulos exteriores é insuficiente para explicar a complexidade do conhecimento gramatical que, relativamente cedo, vem a dominar) e o de que as crianças de origens e contextos sociais e geográficos completamente distintos adquirem essencialmente o mesmo tipo de conhecimento linguístico, passando exactamente pelas mesmas fases de desenvolvimento, a ritmos semelhantes. Deste ponto de vista, a linguagem é vista como uma construção mental (e não social, como para Saussure) e a linguística, em última análise, como um ramo da psicologia cognitiva. (Pedro Santos)
cidadania, teorias da
As teorias da cidadania respondem de maneira diferente à pergunta “Como devemos organizar a sociedade de modo a potenciar a participação dos cidadãos no processo de decisão política?" Há cinco teorias centrais.
O republicanismo aristotélico é a teoria que defende que os cidadãos têm o dever de participar na vida política, e que só essa participação pode realizá-los como seres humanos. A teoria dos direitos defende que a participação dos cidadãos na vida pública emerge quando o estado lhes garante direitos civis, políticos e sociais. Os direitos civis incluem coisas como o direito a não ser discriminado em função da raça, religião ou sexo; os políticos, o direito de votar, de ter filiação partidária e de concorrer a eleições; e os sociais, o direito à educação, à saúde, ao trabalho e à reforma. A teoria conservadora defende que a participação dos cidadãos resulta da imersão na vida económica e da compreensão dos mecanismos do mercado, sendo necessário que o estado cancele grande parte dos direitos sociais. A teoria da sociedade civil defende que os cidadãos aprendem a participar na vida pública participando em associações cívicas, nas quais aprendem as virtudes cívicas, e através das quais intervêm na vida pública. A teoria da virtude liberal defende que só o ensino das virtudes liberais dará aos cidadãos a motivação e os conhecimentos necessários para participar na vida pública.
Os aspectos centrais de cada uma destas teorias são suficientemente vagos para se poder combinar mais de uma teoria. Podemos, por exemplo, defender que a escola desempenha um papel crucial na formação do cidadão, mas ao mesmo tempo defender a importância das associações cívicas e da responsabilização económica. (Desidério Murcho)
ciência
As disciplinas que agrupamos sob a designação “ciência" incluem as ciências formais e as ciências empíricas (ver empírico).
As principais ciências formais, assim chamadas pelo facto de os seus objectos de estudo não terem existência concreta (ver abstracto e concreto), são a matemática e a lógica.
As ciências empíricas são aquelas que estudam, com base na experiência, os fenómenos naturais e sociais. A finalidade de tais ciências é descobrir e explicar os padrões e regularidades desses fenómenos, enunciando-os rigorosamente sob a forma de leis. As leis genuinamente científicas 1) constituem generalizações corroboradas acerca dos fenómenos que descrevem, 2) permitem realizar previsões rigorosas e 3) são passíveis de ser testadas. Estas três características diferenciam-nas dos enunciados da filosofia, da religião, do senso comum e das pseudociências (como a alquimia, a astrologia ou a parapsicologia). Outro aspecto que diferencia a ciência dos demais saberes, e também das pseudociências, é o recurso sistemático a métodos formais de prova. Saber se as ciências sociais têm por objectivo, como as naturais, a elaboração de leis, é ponto de discórdia entre os especialistas.
O conjunto de procedimentos dos cientistas no seu trabalho constitui o método científico. Em filosofia da ciência discute-se se existe um método científico único e como poderemos descrevê-lo apropriadamente, sendo particularmente importantes a este respeito os trabalhos de Imre Lakatos (1922–1974), Karl Popper, Paul Feyerabend e Thomas Khun.
A cisão moderna entre a filosofia e a ciência dá-se progressivamente com os trabalhos de Copérnico (1473–1543), Kepler (1571–1630), Galileu e Newton (1642–1727), que impulsionaram decisivamente o recurso à experimentação e a matematização da ciência. Ver explicação científica, observação, método científico, método experimental, método hipotético-dedutivo, corroboração, generalização, problema da indução, verificacionismo, verificabilidade, falsibicabilidade, falsificacionismo, critério de demarcação, positivismo e Comte. (António Paulo Costa)
ciência, filosofia da
Ver filosofia da ciência.
científico, método
Ver método científico.
coerentismo
Perspectiva epistemológica (ver epistemologia), segundo a qual o nosso conhecimento não carece de qualquer tipo de fundamento. O conhecimento é antes encarado à maneira de uma teia ou sistema de crenças coerentes entre si, que se sustentam mutuamente, dispensando qualquer necessidade de uma crença — ou de um conjunto de crenças — em que todas as outras se apoiem. O filósofo austríaco Otto Neurath (1882–1945) ilustra esta perspectiva com uma célebre metáfora, conhecida como Barco de Neurath: tal como é possível a um barco navegar sem se afundar, apesar de ser composto de inúmeras partes e de nenhuma delas suportar todas as outras, o mesmo acontece com o conhecimento. Cada uma das nossas convicções é como cada uma das peças do barco. Ligadas umas às outras, formam uma totalidade consistente e auto-sustentada. Este é o modo como, de facto, se estrutura a justificação das nossas crenças, demarcando-se o coerentismo tanto do cepticismo como do fundacionalismo. Para um céptico, é impossível encontrar justificações satisfatórias para as nossas crenças, coisa que um coerentista rejeita; para um fundacionalista, as nossas crenças justificam-se a partir de um número limitado de crenças mais evidentes e fundamentais, como sustenta Descartes com o célebre cogito ergo sum, coisa que o coerentismo também rejeita. (Aires Almeida)
cogito
Nome por que é conhecido o famoso argumento (segundo alguns) ou afirmação (segundo outros) de Descartes “penso, logo existo” e que em latim é “cogito ergo sum”.
cogito ergo sum
Expressão latina utilizada por Descartes que significa “penso, logo existo”. Ver também dúvida metódica.
cognitivismo estético
Perspectiva filosófica acerca da arte, segundo a qual ela tem valor na medida em que serve para aumentar o nosso conhecimento. O cognitivismo estético é uma teoria funcionalista (ou instrumentalista), pois reconhece que a arte tem uma função, ao contrário do esteticismo. Um dos mais destacados defensores do cognitivismo estético é o filósofo americano Nelson Goodman. Ver também funcionalismo estético. (Aires Almeida)
compatibilismo e incompatibilismo
O problema do livre-arbítrio consiste em saber se a crença de que somos livres é compatível com a crença de que o mundo é governado por leis e que no mundo todos os acontecimentos, incluindo as nossas acções, são determinados pelas suas causas (ver causa e efeito). Em geral, existem dois tipos de teorias que respondem a este problema: as teorias compatibilistas e as teorias incompatibilistas.
O compatibilismo é uma concepção metafísica que afirma que o livre-arbítrio é compatível com o determinismo. A posição compatibilista pode ser expressa com a seguinte afirmação condicional: se tudo for determinado, é possível que exista livre-arbítrio.
O determinismo moderado é a teoria compatibilista mais influente. Um determinista moderado, como David Hume, aceita que a acção seja determinada por causas; no entanto, sustenta que essa acção pode ser livre se o agente, ao praticá-la, puder agir de outra forma e se tiver um controlo sobre o desejo e a crença que causam a acção. Por exemplo, entregar um telemóvel a um ladrão é uma acção livre caso nos seja possível recusar fazê-la e se o desejo de viver, assim como a crença de que entregar o telemóvel permite preservar a vida, forem as causas dessa acção.
O incompatibilismo é o conjunto de concepções metafísicas que negam que o livre-arbítrio seja compatível com o determinismo. A posição dos incompatibilistas é a seguinte: se tudo for determinado, não é possível que exista livre-arbítrio. As duas teorias incompatibilistas mais importantes são o determinismo radical e o libertismo. Os deterministas radicais argumentam que o livre-arbítrio não existe porque todas acções são efeito de causas remotas e incontroláveis. Os libertistas afirmam que o livre arbítrio existe porque nem todas as acções são o efeito de causas remotas e incontroláveis. (António Paulo Costa)
composição, falácia da
Ver falácia da composição.
compreensão
Segundo a chamada lógica de Port-Royal, a compreensão é o conjunto de atributos que são consequência semântica de um termo ou conceito. Assim, atributos como substância, material, viva e sensível constituem a compreensão do conceito animal. A compreensão de um termo ou conceito distingue-se da sua extensão. Esta é o conjunto de indivíduos ou entidades a que o termo ou conceito se aplica. A extensão do conceito de animal inclui todo e qualquer animal que exista, tenha existido ou venha a existir. A compreensão de um termo ou conceito não é alterada pelo número de indivíduos a que se aplique esse conceito: o conceito de animal permanece o mesmo quer se aplique a um indivíduo, a milhões de indivíduos ou a nenhum indivíduo. Ver extensão, intensão. (Luís Rodrigues)
Comte, Auguste (1798–1857)
Filósofo francês, pai do positivismo do séc. XIX. É também considerado um dos fundadores da sociologia. Comte chamava à sua filosofia “positiva” porque acreditava no progresso do conhecimento em todos os domínios, procurando identificar os diferentes estados ou fases por que as nossas concepções do mundo tiveram de passar até chegar ao seu estado definitivo. Os três estados são o teológico, o metafísico e o positivo. No primeiro, procuravam-se as causas primeiras de todos os fenómenos, recorrendo-se a entidades sobrenaturais e a explicações de tipo religioso. No segundo, as nossas concepções evoluíram no sentido de substituir as entidades sobrenaturais por forças abstractas. No estado positivo ou científico, o “espírito humano” deixa de querer conhecer “as causas íntimas dos fenómenos, para se dedicar apenas à descoberta, pelo uso bem combinado do raciocínio e da observação, das suas leis efectivas, isto é, das suas relações invariáveis de sucessão e similitude”. Para Comte só a ciência pode satisfazer adequadamente a nossa necessidade de conhecimento, já que só a ciência é capaz de formular leis da natureza e de fazer previsões apoiadas em dados empíricos. As ideias de Comte foram muito criticadas, mas também influenciaram filósofos tão importantes como Stuart Mill. Curso de Filosofia Positiva (1830–42) é o título da sua obra mais importante. (Aires Almeida)
conceito
Os constituintes dos pensamentos (ou proposições). A proposição de que Lisboa é uma bela cidade, tem como um dos seus constituintes o conceito de cidade. Possuir um conceito é saber usá-lo. Por exemplo, se alguém apontar para uma bola e disser que é um tigre é porque não possui o conceito de tigre; mas se for competente no uso do termo “tigre”, possuiu o conceito em causa. Uma das muitas questões em aberto é a de saber se os conceitos são entidades abstractas independentes da mente ou se dependem desta para existirem. (Célia Teixeira)
conceito aberto e conceito fechado
Um conceito é aberto se não houver um conjunto de características fixas, ou condições necessárias e suficientes, a partir das quais ele possa ser definido, isto é, a partir das quais se torna possível encontrar a sua extensão. Caso seja possível apresentar um conjunto de características fixas capazes de identificar os objectos que fazem parte da extensão de um dado conceito, então esse conceito é fechado. Isto significa que um conceito aberto é reajustável, podendo ser corrigido de modo a alargar o seu uso a casos completamente novos. Esta noção surgiu com o filósofo austríaco Wittgenstein, que deu como exemplo o conceito de jogo. Segundo Wittgenstein, não é possível identificar um conjunto fixo de características comuns a todos os jogos, além de que podem ser inventados jogos com características completamente diferentes dos que já existem. O mesmo se passa, segundo o filósofo americano Morris Weitz (1916-87), com o conceito de arte, até porque a arte é sempre criativa e inovadora. Por isso, a arte também não pode ser definida em termos de condições necessárias e suficientes. Ver também parecença familiar. (Aires Almeida)
conclusão
A afirmação que se defende, num argumento, recorrendo a premissas. Por exemplo, a conclusão do argumento “Os animais não têm direitos porque não têm deveres” é a afirmação “Os animais não têm direitos”. (Desidério Murcho)
condição necessária
Uma condição necessária para ser F garante que tudo o que for F satisfaz essa condição, mas não garante que tudo o que satisfaz essa condição é F (não é uma condição suficiente). Por exemplo, ser grego é uma condição necessária para ser ateniense, mas não é uma condição suficiente, já que se pode ser grego sem ser ateniense. Uma condição necessária é expressa pela consequente de uma condicional; por exemplo: se alguém é ateniense, é grego. Numa afirmação com a forma “Todo o F é G”, o G é uma condição necessária de F; por exemplo: todos os atenienses são gregos. Ver definição explícita. (Desidério Murcho)
condição necessária e suficiente
Uma condição necessária e suficiente para ser F garante a coincidência entre F e essa condição. Por exemplo, uma condição necessária e suficiente para ser água é ser H2O. Isto significa que tudo o que for H2O é água, e tudo o que for água é H2O. Exprime-se muitas vezes uma condição necessária e suficiente usando uma bicondicional; por exemplo: Sócrates era ateniense se, e só se, nasceu em Atenas. Encontrar condições necessárias e suficientes é o objectivo da definição explícita e parte integrante de uma compreensão aprofundada das coisas. (Desidério Murcho)
condição suficiente
Uma condição suficiente para ser F garante que tudo o que satisfaz essa condição é F, mas não garante que tudo o que é F satisfaz essa condição (não é uma condição necessária). Por exemplo, ser ateniense é uma condição suficiente para ser grego, mas não é uma condição necessária, já que se pode ser grego sem ser ateniense. Uma condição suficiente é expressa pela antecedente de uma condicional; por exemplo: se alguém é ateniense, é grego. Numa afirmação com a forma “Todo o F é G”, o F é uma condição suficiente de G; por exemplo: todos os atenienses são gregos. Ver definição explícita. (Desidério Murcho)
condicional (→)
Uma afirmação com a forma “Se P, então Q”, como “Se a música é arte, é bela”. Chama-se “antecedente” a P e “consequente” a Q. No discurso corrente usa-se muitas vezes condicionais como formas extremamente abreviadas de modus tollens ou modus ponens: “Se Deus não existisse, não poderia haver universo” pode ser uma forma abreviada de argumentar a favor da conclusão omitida “Deus existe”, omitindo também a premissa (“Há universo”). E “Se a dor tem importância moral, não devemos maltratar os animais” pode ser uma forma abreviada de argumentar a favor da conclusão “Não devemos maltratar os animais”, omitindo também a premissa “A dor tem importância moral".
Na lógica clássica, encara-se uma condicional como uma afirmação que só é falsa caso a antecedente seja verdadeira e a consequente falsa. Isto provoca problemas (discutidos em filosofia da linguagem), pois em muitas circunstâncias achamos que uma condicional com antecedente e consequente falsa não é verdadeira, como afirma a lógica clássica, mas sim falsa: “Se Durão Barroso é francês, é asiático” é intuitivamente falsa, mas do ponto de vista da lógica clássica é verdadeira, dado que a sua antecedente é falsa. Intuitivamente, é-se levado a pensar que esta condicional é falsa porque a interpretamos como um caso particular da seguinte condicional geral: “Se alguém é francês, é asiático”. Dado que esta condicional geral é efectivamente falsa (é equivalente à afirmação universal falsa “Todos os franceses são asiáticos”), é-se levado a pensar que a primeira também o é. Quando as condicionais gerais associadas às particulares são verdadeiras, as intuições linguísticas não diferem da definição clássica da condicional: a condicional “Se Sócrates é lisboeta, é português” é intuitivamente verdadeira (porque “Se alguém é lisboeta, é português” é verdadeira) e é verdadeira segundo a lógica clássica (porque a antecedente é falsa).
As condicionais tipicamente usadas em filosofia exprimem conexões conceptuais. Uma condicional como “Se Kant vivia numa ilha, era um ilhéu” é intuitivamente verdadeira, porque há uma conexão conceptual entre viver numa ilha e ser ilhéu que garante a verdade da seguinte condicional: “Se alguém vive numa ilha, é um ilhéu”. Assim, para negar uma condicional filosófica como “Se Deus existe, a vida faz sentido”, não é necessário provar que é verdadeiro que Deus existe e falso que a vida faz sentido; basta mostrar que não há conexão conceptual entre a antecedente e a consequente da condicional — isto é, que seria conceptualmente possível existir Deus apesar de a vida não ter sentido. (Desidério Murcho)
Murcho, Desidério, O Lugar da Lógica na Filosofia, Cap. 4 (Lisboa: Plátano, 2003).
Newton-Smith, W. H., Lógica: Um curso introdutório, Cap. 2 (Lisboa: Gradiva, 1998).
Priest, Graham, Lógica, Cap. 7 (Lisboa: Temas e Debates, 2002).
condições de verdade
Ver tabela de verdade.
conectiva
Aquelas expressões que servem para gerar frases a partir de frases. Por exemplo, a conectiva “e”, quando colocada entre duas frases (por exemplo, “Aristóteles é um filósofo” e “Aristóteles foi aluno de Platão”), gera a seguinte frase complexa: “Aristóteles é um filósofo e foi aluno de Platão”. As conectivas são classificadas em função do número mínimo de frases que podem ligar. Por exemplo, as conectivas como “e” e “ou”, são binárias pois precisam no mínimo de duas frases para gerar uma frase complexa. Já a conectiva “não” é unária, pois apenas precisa de uma frase para formar outra. Por exemplo, se juntarmos “não" à frase “Aristóteles é um filósofo” ficamos com a seguinte frase falsa: “Aristóteles não é um filósofo”. As conectivas mais usadas são as verofuncionais (ver operador verofuncional): “e”, “ou”, “não” e “se, então” apesar de ser discutível se esta última é verofuncional (ver condicional). (Célia Teixeira)
confirmação
Num bom argumento indutivo (ver indução), as premissas confirmam a conclusão num grau elevado. Por exemplo, se observamos muitos corvos e constatamos que não há um único que não seja negro, encontramos assim dados que confirmam a hipótese de que todos os corvos são negros. Obviamente, não podemos ter a certeza de que esta hipótese é verdadeira, mas à medida que vamos observando cada vez mais corvos negros a probabilidade de a hipótese ser verdadeira (isto é, o seu grau de confirmação) vai aumentando. Ver implicação, corroboração. (Pedro Galvão)
conhecimento
Os verbos conhecer e saber são sinónimos e costumam ser utilizados de três maneiras diferentes. Na frase “a Ana sabe nadar”, o termo “sabe” serve para atribuir à Ana uma determinada competência ou capacidade; por sua vez, na frase “a Ana conhece o primeiro-ministro” o termo “conhece” significa que a Ana é capaz de identificar alguém (ou algo), ou também pode significar que ela tem ou teve algum tipo de contacto com essa pessoa (ou coisa); finalmente, na frase “a Ana sabe que Paris é a capital da França”, o que se afirma que a Ana sabe é algo que tanto pode ser verdadeiro como falso. Neste último caso, o que vem a seguir a “sabe que” é uma outra frase que exprime uma proposição. Este é o sentido proposicional de “conhecer” que é objecto de estudo da epistemologia. Não existe uma definição satisfatória de “conhecimento”, mas há pelo menos três condições necessárias que, em geral, os filósofos aceitam: não há conhecimento sem crença; a crença tem de ser verdadeira; além de verdadeira, a crença tem também de ser justificada. Quer isto dizer que não podemos conhecer algo em que não acreditamos; que não podemos conhecer falsidades; e que não há conhecimento se as nossas crenças, apesar de verdadeiras, não forem justificadas. (Aires Almeida)
conjunção (∧)
Qualquer afirmação com a forma “P e Q”, como “Deus existe e a vida tem sentido”. Uma conjunção é verdadeira se, e só se, ambas as proposições, P e Q, que a constituem forem verdadeiras. Em qualquer outra circunstância é falsa. É preciso ter em consideração que não se está a falar de conjunção em sentido gramatical. Assim, frases com as formas “P mas Q”, “P, apesar de Q”, “Não só P como Q”, ou “P, Q e R” são conjunções. Por outro lado, frases como “Dá-me uma cerveja e eu fico feliz”, que são superficialmente conjunções, não o são de facto (neste caso, trata-se de uma condicional: “Se me deres uma cerveja, eu fico feliz”. (Aires Almeida)
conotação
1.Termo equivalente ao mais corrente “intensão”.
2. Frequentemente, diz-se que um termo tem certo tipo de conotações se estiver tipicamente associado a ideias, modos de pensar ou práticas expecíficas (por exemplo, o termo “alma”, ao contrário do termo “mente”, tem conotações religiosas). Ver também compreensão, denotação, sentido. (Pedro Santos)
consciência moral
O reconhecimento do carácter moral de algumas das nossas acções. Uma pessoa com consciência moral é alguém que sabe que algumas das suas acções podem ser boas ou más, morais ou imorais e que tem isto conta quando age. Pelo contrário, uma pessoa sem consciência moral é alguém que não tem em conta esse aspecto das suas acções. Por exemplo, uma pessoa sem consciência moral poderá roubar outra pessoa sem ter em consideração o facto de o seu acto ser imoral. Ver ética, egoísmo psicológico. (Desidério Murcho)
consequência
1. (⊨) Uma proposição P é uma consequência de um dado conjunto de proposições quando P se pode concluir validamente desse conjunto de proposições (ver validade e invalidade). Ter atenção às consequências das nossas afirmações é muito importante, pois por vezes elas têm consequências indesejadas. Por exemplo, afirmar que tudo é relativo tem como consequência que isto que se está a dizer também é relativo, o que derrota a própria ideia que se queria defender.
2. Noutros contextos, usa-se o termo “consequência" como sinónimo de “efeito”, nomeadamente efeito causal. Por exemplo, uma bola move-se em consequência de um pontapé. (Desidério Murcho)
consequencialismo
O consequencialismo é a perspectiva normativa segundo a qual as consequências das nossas opções constituem o único padrão fundamental da ética. Esta perspectiva corresponde a um conjunto muito abrangente e diversificado de teorias da obrigação moral, do certo e do errado, e não há um acordo perfeito quanto às condições que uma teoria tem de satisfazer para ser classificada como “consequencialista”. (O egoísmo ético, por exemplo, nem sempre é considerado uma versão de consequencialismo.) No entanto, as teorias consequencialistas mais puras exibem seguramente três características importantes. Em primeiro lugar, aplicam-se directamente a actos individuais. Em segundo lugar, prescrevem a maximização do bem, isto é, afirmam que os agentes morais estão sob a obrigação permanente e ilimitada de dar origem aos melhores estados de coisas ou situações. Em terceiro lugar, pressupõem uma teoria do valor que resulta numa avaliação dos estados de coisas em termos estritamente impessoais.
De acordo com a interpretação prevalecente, mas objectável, o utilitarismo clássico de Jeremy Bentham (1789) e J. S. Mill (1861) (e em certa medida também de Henry Sidgwick (1907)) exibe estas três características. Pressupondo uma teoria hedonista do valor, segundo a qual o prazer é o único bem fundamental e a dor o único mal, os utilitaristas clássicos terão defendido que agir acertadamente é escolher, entre as opções disponíveis, aquela que resulta no maior total de prazer.
Os utilitaristas distinguem-se dos demais consequencialistas em virtude do tipo de teoria do valor em que se baseiam. O utilitarismo parte sempre de uma teoria welfarista do valor, ou seja, sustenta que o bem a promover consiste exclusivamente no bem-estar dos indivíduos que poderão ser afectados pela nossa conduta. Obviamente, o utilitarista não tem de advogar uma concepção hedonista do bem-estar: pode, como R. M. Hare (1981), identificar o bem-estar com a satisfação de desejos ou preferências, ou, à semelhança de G. E. Moore (1903), conceber o bem-estar em termos de uma pluralidade irredutível de valores, como a virtude, o conhecimento, a fruição estética e a amizade. No entanto, o utilitarista supõe sempre que só as entidades dotadas de estados mentais conscientes possuem bem-estar no sentido relevante: só essas entidades têm uma vida que pode ser boa ou má para si próprias. O consequencialista que inclui, por exemplo, a preservação dos ecossistemas entre os bens fundamentais a promover, rejeita o utilitarismo.
Afirma-se por vezes que, além de welfarista, a teoria do valor pressuposta em qualquer versão de utilitarismo tem de ser agregacionista: a avaliação dos estados de coisas deverá ser indiferente à distribuição do bem, consistindo no simples apuramento do bem total através da soma dos custos e benefícios para todos os indivíduos afectados.
De acordo com o consequencialismo objectivo ou actualista, o acto certo ou obrigatório é sempre aquele que efectivamente maximiza o bem, independentemente daquilo que o agente previu ou poderia ter previsto. O consequencialismo subjectivo ou probabilista, pelo contrário, identifica o acto obrigatório atendendo à perspectiva epistémica do agente: agir correctamente é seguir o curso de acção que, ponderadas as probabilidades à luz dos dados disponíveis, se apresenta mais promissor. Imagine-se, por exemplo, que um cirurgião pode escolher entre (A) uma operação extremamente arriscada mas que, em caso de sucesso, produzirá uma cura total e (B) uma operação com riscos negligenciáveis que produzirá seguramente uma cura quase total. Um consequencialista subjectivo dirá que o acto acertado é realizar a operação B. Mas suponha-se que o cirurgião opta pela operação A e que, contrariamente ao que seria de esperar, o paciente sobrevive e fica curado. Um consequencialista objectivo, como Hare, dirá que esse acto foi acertado.
Este exemplo pode sugerir que na sua versão objectiva o consequencialismo é demasiado contra-intuitivo para ser levado a sério. Mas importa agora observar que o consequencialismo costuma ser entendido explicitamente não como uma perspectiva sobre a forma correcta de tomar decisões morais, mas como um padrão que visa indicar as propriedades ou factores que tornam uma acção moralmente certa ou errada. Assim, o consequencialista objectivo pode reconhecer que o cirurgião realizou o acto acertado, mas acrescentar que esse acto resultou de uma decisão que não foi razoável ou racional e que, portanto, a sua conduta nada tem de louvável.
Para afastar a objecção ingénua segundo a qual o consequencialismo implica um modo de vida insustentavelmente calculista, basta perceber precisamente que este não consiste num procedimento de decisão, e que, por isso, não implica que os agentes devem estar sempre embrenhados na ponderação dos custos e benefícios dos diversos cursos de acção disponíveis em cada momento. No entanto, isto não significa que o consequencialismo nada nos possa dizer sobre a tomada de decisões — se fosse esse o caso, o próprio interesse prático desta perspectiva seria muito questionável.
Para tornar isto claro, vale a pena destacar as teorias consequencialistas que, como a de Hare, distinguem dois níveis diferentes de pensamento moral. Hare defende que, em virtude das nossas limitações cognitivas, o pensamento moral humano deve situar-se quase sempre no nível intuitivo: neste nível permanecemos indiferentes ao padrão consequencialista e limitamo-nos a agir em função das disposições e intuições que se exprimem nas regras morais simples habitualmente reconhecidas, isto é, limitamo-nos a seguir de perto a “moralidade comum”. No entanto, por vezes as regras morais entram em conflito. Precisamos de resolver dilemas — e precisamos também de determinar que intuições e disposições devemos inculcar e cultivar. Para estes efeitos, e só para estes efeitos, devemos ascender ao nível crítico do pensamento moral. É neste nível que tomamos decisões raciocinando de forma abertamente consequencialista. Esta distinção entre níveis de pensamento dá origem à seguinte perspectiva: os agentes morais não devem colocar-se acima da moralidade comum recorrendo sistematicamente ao padrão consequencialista para tomar todo o tipo de decisões, mas esse padrão tem uma relevância prática significativa, pois serve tanto para reformar a moralidade comum através do exame crítico das práticas que a sustentam como para fornecer orientação onde esta colapsa em conflitos de deveres.
Existem duas objecções fundamentais ao consequencialismo que apontam o seu carácter fortemente contra-intuitivo. Segundo a objecção da integridade (veja-se Scheffler: 1994), o consequencialismo é uma perspectiva demasiado exigente: implica que devemos dedicar todos os nossos recursos à promoção estritamente imparcial do bem, de tal maneira que qualquer acto que não maximize o bem terá de ser considerado errado. Na prática, isto significa que é moralmente errado fazer coisas como comprar um bilhete de cinema ou praticar desportos náuticos, pois o dinheiro ou o tempo assim despendidos poderiam ser canalizados para actividades mais proveitosas de um ponto de vista impessoal. Dada a extrema exigência do consequencialismo, alegam os críticos, este aliena o agente dos seus projectos e compromissos pessoais, ameaçando assim a sua integridade enquanto indivíduo autónomo.
De acordo com a objecção dos direitos, o consequencialismo falha também pela razão inversa, isto é, por propor um padrão moral demasiado permissivo. O exemplo mais utilizado para ilustrar este ponto é talvez o do transplante: para salvar cinco pacientes que estão prestes a morrer devido à falta de órgãos para transplante, um cirurgião mata outro paciente e usa os seus órgãos para os salvar. Embora este acto seja intuitivamente abominável, o consequencialismo parece sancioná-lo, pois não reconhece a existência de quaisquer direitos que imponham limites àquilo que é permissível fazer em nome do maior bem.
Podemos destacar três estratégias gerais para lidar com estas objecções. A primeira consiste em mitigar o peso das intuições morais através do recurso à distinção entre níveis do pensamento moral. Hare desenvolve esta estratégia da seguinte maneira: se considerarmos apenas situações realistas — as únicas relevantes para o pensamento intuitivo — o consequencialismo não implica, por exemplo, que o cirurgião deve matar o paciente para aproveitar os seus órgãos; só no nível crítico encontramos casos hipotéticos suficientemente idealizados para a obtenção de resultados contra-intuitivos, mas a este nível as intuições não têm a menor força probatória e, portanto, a ideia de que em certas circunstâncias muito específicas o cirurgião deveria matar o paciente não milita contra o consequencialismo.
A segunda estratégia consiste em advogar uma versão indirecta de consequencialismo. Em vez de aplicar directamente o seu padrão normativo a actos, o consequencialista pode eleger outro tipo de ponto focal — por exemplo, regras, motivos ou traços de carácter. O consequencialismo das regras, cujo representante mais influente é talvez R. B. Brandt (1979), é a opção mais frequente. Segundo esta perspectiva, o estatuto moral de um acto depende da sua conformidade a regras, de tal maneira que um acto é errado se, e apenas se, estiver em desacordo com as regras morais correctas. E as regras morais são correctas apenas em virtude de a sua observância geral promover imparcialmente o bem. O consequencialista das regras pode condenar o cirurgião e absolver o praticante de desportos náuticos: dirá que o primeiro transgride uma regra vital para o bem-estar da sociedade, mas que a conduta do segundo está em conformidade com todas as regras sancionadas pelo padrão consequencialista.
A terceira estratégia consiste na adopção de uma teoria do bem que evite os resultados contra-intuitivos. Imagine-se, por exemplo, um “consequencialismo dos direitos”, ou seja, uma perspectiva consequencialista baseada na tese segundo a qual a melhor situação de um ponto de vista impessoal é aquela em que menos direitos são violados. Poder-se-ia alegar que o cirurgião — mas não o desportista — procedeu erradamente: ao matar o paciente violou o direito à vida de uma pessoa, mas não teria violado qualquer direito à vida caso tivesse deixado morrer os cinco pacientes.
Note-se que qualquer uma destas estratégias para responder às objecções da integridade e dos direitos requer uma justificação apropriada. Por que razão teremos de ignorar as intuições quando nos situamos no nível crítico do pensamento moral? Por que razão deveremos eleger um ponto focal como as regras em vez de aplicarmos o padrão consequencialista a actos? Ou por que razão deixar morrer alguém não deve contar como uma violação de um direito? Mesmo que esteja em conformidade com as nossas intuições onde isso pareça desejável, uma perspectiva consequencialista satisfatória não pode ser meramente ad hoc — tem de justificar as opções teóricas que asseguram tal conformidade.
Hare tentou justificar o consequencialismo a partir da universalizabilidade dos juízos morais; J. C. Harsanyi (1978) recorreu à teoria bayesiana da decisão para o mesmo efeito; mais recentemente, P. Pettit (1991) argumentou a favor da perspectiva salientando a sua elevada parcimónia. Apesar de os fundamentos do consequencialismo serem ainda objecto de grande controvérsia, esta perspectiva permanece muito influente, até porque as principais perspectivas rivais — a ética deontológica e a ética das virtudes — enfrentam problemas teóricos pouco invejáveis. No domínio da ética prática ou aplicada, as abordagens consequencialistas, em grande medida devido à influência de Peter Singer, continuam a florescer. Ver também deontologia, utilitarismo, valor, virtude. (Pedro Galvão)
Bentham, J. (1789), An Introduction to the Principles of Morals and Legislation, Oxford University Press, Oxford (1996).
Brandt, R. B. (1979), A Theory of the Good and the Right, Prometheus, Londres. Darwall, S. (2003) (org.), Consequentialism, Blackwell, MA.
Hare, R. M. (1981), Moral Thinking, Clarendon Press, Oxford.
Harsanyi, J.C. (1978) “Bayesian Decision Theory and Utilitarian Ethics”, in S. Darwall, Consequentialism, Blackwell, Oxford, (2003), págs. 197-206.
Mill. J. S. (1861), Utilitarismo. Tradução de Pedro Galvão, Porto Editora, Porto (2004).
Moore, G. E. (1903), Principia Ethica, Cambridge University Press, Cambridge (1993).
Parfit, D. (1984), Reasons and Persons, Oxford University Press, Oxford.
Pettit, P. (1991) “Consequentialism" in P. Singer, A Companion to Ethics, Blackwell, Oxford, págs. 230–240.
Scheffler, S. (1994), The Rejection of Consequentialism, ed. rev., Oxford University Press, Oxford.
Sidgwick, H. (1907), The Methods of Ethics, 7.ª ed., Hackett, Indianapolis e Cambridge (1981).
Singer, P. (1993), Ética Prática, Gradiva, Lisboa (2000).
consistência e inconsistência
Duas ou mais proposições são consistentes se, e só se, podem ser simultaneamente verdadeiras; e são inconsistentes se, e só se, não podem ser simultaneamente verdadeiras. Por exemplo, as afirmações “Deus existe” e “Sócrates era um filósofo” são consistentes; e as afirmações “Deus existe” e “Deus não existe” são inconsistentes. Nem sempre é fácil saber quando duas proposições são consistentes ou inconsistentes. A mais leve complexidade lógica pode provocar enganos. Por exemplo, há razões para pensar que as afirmações “Todos os lobisomens são peludos” e “Nenhum lobisomem é peludo” não são inconsistentes; mas, intuitivamente, estas afirmações parecem inconsistentes. Note-se que a lógica aristotélica não se aplica a proposições que contenham classes vazias, como “lobisomens”; se excluirmos as classes vazias, quaisquer duas proposições com a forma “Todo o A é B” e “Nenhum A é B” serão efectivamente inconsistentes (ver quadrado de oposição).
Outras vezes, é muito difícil saber se duas proposições são consistentes ou não. Por exemplo, em filosofia discute-se o chamado problema do mal, que consiste em saber se as duas afirmações seguintes são consistentes: “Deus existe e é omnipotente, omnisciente e sumamente bom” e “Há mal no mundo”.
Não se deve confundir inconsistência com contradição; todas as contradições são inconsistências, mas nem todas as inconsistências são contradições. Por exemplo, uma vez que há seres humanos, as afirmações “Todos os seres humanos são mortais” e “Nenhum ser humano é mortal” são inconsistentes, mas não são contraditórias entre si. Não se deve igualmente dizer que uma teoria ou proposição “é consistente com o mundo”; as teorias ou proposições só podem ser consistentes entre si e não com o mundo. Relativamente ao mundo, as teorias e proposições são verdadeiras ou falsas, consoante descrevem fielmente ou não o modo como as coisas são. (Desidério Murcho)
contexto
A realidade, situação ou linguagem que rodeia a enunciação de uma palavra, frase ou discurso (ver discursivo) de que pode depender a determinação do seu significado e, em última instância, a sua interpretação e compreensão. Numa frase como “Hoje ofereci-lhe um ramo de flores”., aquilo que “hoje” e “lhe” referem e, consequentemente, o significado da frase e o valor de verdade da proposição que a frase exprime, dependem do seu contexto de uso (quando é enunciada, quem a enuncia, a quem a frase se refere, etc.). Para eliminar a ambiguidade de certos termos, como “aqui”, e frases, como “O Speedy é do outro mundo" tem de se ter em conta o contexto em que esses termos e frases são usados. Ver indexical, uso e menção. (Álvaro Nunes)
contingente
Ver necessário e contingente.
continuidade e descontinuidade
A expressão “continuidade e descontinuidade" (ou “continuidade e ruptura”) tem sido usada para referir três problemas diferentes de filosofia da ciência: 1) o problema da demarcação, que consiste em saber se existe e qual é o critério que estabelece a fronteira entre, por um lado, o conhecimento científico e, por outro, o conhecimento não científico (como o senso comum, a filosofia ou a religião) e pseudocientífico (como a parapsicologia, a alquimia e a astrologia); 2) o problema da unidade da ciência, em que se discute se existe e qual é a descrição apropriada de um único método científico comum às várias ciências; 3) o problema do desenvolvimento das ciências, que consiste em discutir se existe continuidade ou ruptura entre diferentes estádios de desenvolvimento das ciências, e até entre estes e os estádios pré-científicos. A propósito de 1, ver explicação científica, critério de demarcação, verificabilidade, verificacionismo, corroboração, falsibicabilidade e Popper; a propósito de 2, ver método experimental, método hipotético-dedutivo, Galileu Galilei, positivismo, Comte e Paul Feyerabend; a propósito de 3, ver Popper, paradigma, incomensurabilidade e Thomas Kuhn. (António Paulo Costa)
contra-argumento
O objectivo de um contra-argumento é refutar a conclusão estabelecida no argumento de um opositor. Um contra-argumento, que é também um argumento, deverá concretizar pelo menos um dos seguintes objectivos: 1) demonstrar que o argumento do opositor é inválido, isto é, que as premissas não apoiam a conclusão; 2) mostrar que pelo menos uma das premissas do argumento do opositor é falsa; 3) mostrar que a conclusão do argumento do opositor é falsa, ou tem consequências inverosímeis ou contraditórias. Por exemplo, uma forma muito simples de concretizar o primeiro objectivo consiste em imaginar um contra-argumento com a mesma forma lógica do argumento a refutar, mas cujas premissas sejam evidentemente verdadeiras e cuja conclusão seja evidentemente falsa. A validade do argumento “Todas as coisas têm uma causa; logo, há uma causa de todas as coisas” pode refutar-se com o argumento seguinte, obviamente inválido: “Todas as pessoas têm uma mãe; logo, há uma mãe de todas as pessoas”. Ver premissa, conclusão, verdade e falsidade, validade, consequência, contradição, refutação, redução ao absurdo, falácia. (António Paulo Costa)
contradição
1. Uma falsidade lógica; isto é, uma proposição cuja falsidade se pode determinar exclusivamente por meios lógicos. Por exemplo, a afirmação “Sócrates é mortal e não é mortal” é uma contradição.
2. Duas proposições são mutuamente contraditórias quando têm valores de verdade opostos em qualquer circunstância logicamente possível. Por exemplo, as afirmações “Tudo é relativo” e “Algumas coisas não são relativas” são contraditórias. Não se deve confundir inconsistência com contradição; todas as contradições são inconsistências, mas nem todas as inconsistências são contradições. Ver consistência e inconsistência. (Desidério Murcho)
contradição pragmática
Uma contradição entre o que se afirma e a circunstância na qual isso é afirmado. Por exemplo, uma pessoa que grite “Eu não estou a gritar!” está a cair em contradição pragmática. Outros casos menos óbvios incluem alguém que afirme “Não há verdades”; dada a maneira como normalmente usamos a linguagem, esta afirmação parece apresentar-se como uma candidata a ser considerada verdadeira, mas isso contradiz a própria afirmação. Nesse caso, não se compreende bem qual é o objectivo de afirmar tal coisa e os críticos poderão dizer que se trata apenas de uma contradição pragmática. (Desidério Murcho)
contra-exemplo
Um exemplo que se destina a mostrar que uma dada afirmação é falsa. Os contra-exemplos são muito importantes em filosofia, pois são um método eficaz de refutação de teorias (ou afirmações) e uma maneira de as pôr à prova. Por exemplo, será a afirmação “só quem tem deveres pode ter direitos” verdadeira? Um contra-exemplo é que as crianças recém-nascidas não têm deveres, mas têm direitos. Isto mostra que a afirmação anterior é falsa. Muitas vezes encontrar contra-exemplos claros a uma determinada teoria filosófica não é fácil, exigindo-se informação relevante, alguma criatividade e sentido crítico. É importante referir que afirmações como “alguns países europeus que foram no passado colonizadores são hoje ricos” não admitem contra-exemplos. Dizer que Portugal foi colonizador no passado mas não é rico, não é um contra-exemplo. Mas é um contra-exemplo da afirmação universal “todos os países europeus que foram no passado colonizadores são hoje ricos”. Assim, só há contra-exemplos a afirmações universais e condicionais. (Aires Almeida)
contratualismo
O contratualista concebe a ética como uma espécie de acordo ou contrato — as acções são certas ou erradas em virtude de obedecerem ou não aos princípios que seriam objecto do acordo. Alguns contratualistas, como Hobbes, sustentam que o contrato ético é motivado pelo interesse pessoal (ver egoísmo psicológico). Para outros contratualistas, no entanto, a motivação subjacente ao acordo é o respeito recíproco entre pessoas livres e iguais. Além de diferirem entre si quanto à maneira como concebem a motivação do contrato, os contratualistas também divergem no modo como definem as circunstâncias, geralmente idealizadas, em que o mesmo tem lugar. Ver egoísmo ético, Rawls. (Pedro Galvão)
corroboração
Na sua filosofia da ciência, Popper rejeita a indução e, consequentemente, a ideia de que uma hipótese ou teoria científica pode ser confirmada por dados empíricos. Assim, no seu falsificacionismo a noção de confirmação dá lugar à de corroboração. Uma hipótese ou teoria científica é corroborada por dados empíricos quando sobrevive a testes experimentais, isto é, quando não é refutada depois de ter sido posta à prova. E, quanto mais severos são os testes, maior é o grau de corroboração que a teoria adquire. (Pedro Galvão)
crença
O termo é usado para referir 1) um estado mental disposicional, que tem como conteúdo uma proposição, verdadeira ou falsa (ver verdade e falsidade), ou 2) para referir a proposição que constitui o conteúdo desse estado mental. Quando tomamos “crença” na segunda acepção, ela é independente de quem quer que a pense e o estado mental correspondente constitui uma atitude proposicional, uma atitude de crença numa proposição, que envolve certo grau de confiança na verdade dessa proposição (daí a relação próxima entre crença e verdade). O facto de as crenças, enquanto estados mentais, serem disposicionais significa que podemos ter uma disposição para agir de certa forma devido às crenças que temos. Uma concepção comum de filosofia, presente, por exemplo, em Bertrand Russell, vê esta como a análise crítica das crenças (na segunda acepção) instintivas, com o objectivo de determinar quais as justificadas e construir, assim, um sistema coerente de crenças instintivas nas quais todas as outras se fundem. Ver fundacionalismo. (Álvaro Nunes)
critério de demarcação
Critério de acordo com o qual se distinguem as teorias científicas das teorias pseudocientíficas, isto é, daquelas que não sendo científicas procuram passar por tal. O filósofo Karl Popper defende que uma teoria só é científica se puder ser testada. Por sua vez só pode ser testada se for falsificável, coisa que não acontece, segundo Popper, com as pseudociências, como a astrologia e a parapsicologia. Ver também falsificabilidade. (Aires Almeida)
crítica
O acto de examinar cuidadosamente uma obra, teoria ou opinião, procurando determinar se são boas ou verdadeiras e avaliando os argumentos ou ideias em que se apoiam. A filosofia é uma actividade crítica, pois procura-se sempre determinar se as ideias, teorias ou opiniões filosóficas propostas são verdadeiras e se se apoiam em bons argumentos. Para o filósofo, uma opinião que não seja sustentada por bons argumentos, ainda que seja verdadeira, não passa de um preconceito. A crítica não tem de ser negativa. Podemos ser críticos concordando com as opiniões dos outros, desde que encontremos boas razões para concordar com elas. Mas ser crítico implica também ter abertura de espírito para discutir racionalmente as nossas próprias ideias e até para as abandonar, caso não existam boas razões a seu favor. A atitude da pessoa crítica opõe-se à atitude da pessoa dogmática. Ver também dogma. (Aires Almeida)
cultura
1. Conjunto de conhecimentos e práticas aprendidos e ensinados, por contraste com o que é inato. Por exemplo, se um pássaro não tem de aprender a fazer o ninho, fazendo-o instintivamente, então esse ninho não é um produto cultural; mas se tiver de ser ensinado a fazê-lo, então esse ninho é um produto cultural. Os seres humanos são os maiores produtores de cultura do planeta.
2. O conjunto de práticas e de produções materiais, espirituais, artísticas, etc. que servem para identificar um povo ou nação e distingui-lo de outros povos.
3. Opõe-se por vezes a cultura às ciências, usando o primeiro termo para falar das artes e das letras, como a pintura e a poesia. Esta oposição é polémica. (Desidério Murcho)
D
dasein
Termo alemão introduzido por Heidegger e que significa “ser-aí”. Para este filósofo, o ser humano é um ser-aí no sentido em que a sua natureza consiste em estar no mundo. (Desidério Murcho)
datum
Termo latino que significa “dado”: o que é dado nos sentidos, por exemplo. Opõe-se ao que é inferido, nomeadamente com base nos sentidos. Por exemplo, o que eu vejo ao olhar para uma maçã é apenas uma forma e uma cor; mas infiro que é um objecto real com base em vários outros dados, nomeadamente dados de outros sentidos. (Desidério Murcho)
decadentismo
Doutrina estética que coloca a arte acima da ética, defendendo que arte pode mesmo ser imoral, sem que isso lhe retire qualquer valor. É uma doutrina associada às teorias da “arte pela arte”, ou esteticismo. O esteta e escritor irlandês Oscar Wilde (1854–1900) é um dos seus mais ilustres representantes. (Aires Almeida)
dedução
Um argumento cuja validade depende unicamente da sua forma lógica, ou da sua forma lógica juntamente com os conceitos usados. Por exemplo, o argumento seguinte é dedutivo: “Se os animais têm direitos, têm deveres; dado que não têm deveres, não têm direitos”. É dedutivo porque a sua validade depende unicamente da sua forma lógica, que neste caso é a seguinte: “Se P, então Q; não Q; logo, não P”. O argumento seguinte é dedutivo porque a sua validade depende unicamente da sua forma lógica juntamente com os conceitos usados: “A neve é branca; logo, tem cor”. Não é verdadeiro que nos argumentos dedutivos se parta sempre do geral para o particular. O argumento seguinte é dedutivo e tanto a sua premissa como a sua conclusão são particulares: “Alguns filósofos são gregos; logo, alguns gregos são filósofos”. Ver indução. (Desidério Murcho)
definição
Uma maneira de dizer o que uma coisa é. Por exemplo, quando se pergunta o que é a água pode-se responder que é H2O; quando se pergunta o que é o azul pode-se apontar para o céu, o mar, etc. A primeira é uma definição explícita; a segunda é uma definição implícita. Em filosofia, as definições são importantes por duas razões: para que o nosso discurso seja mais claro e como meio para uma compreensão mais substancial dos nossos conceitos mais importantes. Mas as definições filosóficas são objecto de disputa porque são surpreendentemente difíceis de obter. Isto acontece porque os conceitos que queremos definir em filosofia são por vezes tão centrais na nossa economia conceptual que se tornam difíceis de definir. Por exemplo: a física consegue definir “massa”, mas torna-se cada vez mais difícil definir, sem cair em circularidade, os conceitos com que se define a massa, nomeadamente “energia” e “corpo”. E depois será necessário definir os conceitos que usamos para definir esses conceitos, e acabaremos por entrar em problemas filosóficos. As definições que interessam na filosofia são difíceis porque são definições de conceitos tão básicos e centrais que é difícil encontrar outros conceitos mais básicos e mais simples que possamos usar para os definir. (Desidério Murcho)
Murcho, Desidério, “Definição de “Definição"" in A Natureza da Filosofia e o seu Ensino (Lisboa: Plátano, 2002).
definição essencialista
Uma definição que apresenta as condições necessárias e suficientes que algo satisfaz não apenas de facto, mas que é impossível que não satisfaça (ver condição necessária e suficiente). Por exemplo, podemos definir água como H2O; esta é uma definição essencialista porque é impossível que a água não tenha a composição química que tem. As definições essencialistas são importantes em filosofia e correspondem à ideia popular de uma boa definição como algo que capta “a essência” de uma coisa. Imagine-se que se define do seguinte modo criatura com rins: “Criatura com rins é toda a criatura que tem coração”. Enquanto definição essencialista, é uma má definição porque apesar de ser verdade que todas as criaturas que têm rins têm coração, e vice-versa, não é impossível que algumas criaturas com rins não tenham coração, e vice-versa. Talvez noutros planetas outras criaturas com rins não tenham coração; ou talvez tivesse havido na Terra criaturas com rins e sem coração, se a história evolutiva tivesse sido diferente. (Desidério Murcho)
definição explícita
Uma maneira de definir algo por meio de condições necessárias e suficientes (ver condição necessária e suficiente). Por exemplo: “o Homem é um animal racional”; ou: “um estudante transita de ano se, e só se, tiver uma média igual ou superior a 50%”. Há três tipos de definições explícitas: extensionais, essencialistas e analíticas. As definições extensionais limitam-se a procurar dizer o que as coisas são de facto, sem procurar dizer o que as coisas são necessariamente; dado que todos os seres humanos são animais racionais, e que só os seres humanos são animais racionais, esta definição é extensionalmente boa. Mas é uma má definição essencialista, porque não é necessário que todos os animais racionais sejam seres humanos, nem que só os seres humanos sejam animais racionais. E é uma má definição analítica porque a expressão “ser humano” não significa “animal racional" (ver analítico e sintético). As definições explícitas contrastam com as definições implícitas (ver definição implícita). Em filosofia, procuram-se sobretudo definições essencialistas e analíticas dos conceitos filosóficos centrais, como conhecimento, verdade, arte, etc. (Desidério Murcho)
definição implícita
Uma maneira de definir algo sem recorrer a condições necessárias e suficientes (ver condição necessária e suficiente). Por exemplo, para definir a cor verde basta apresentar vários objectos verdes; e podemos compreender o que é a melancolia lendo um romance que descreve uma personagem melancólica, apesar de no romance nunca se dizer explicitamente o que é a melancolia. Há dois tipos de definições implícitas: as ostensivas e as contextuais. Nas ostensivas apresentam-se casos que exemplificam a propriedade que se quer definir (como no caso da cor). Nas contextuais (como no caso do romance) apresentam-se vários contextos nos quais se usa o termo a definir. É um erro tentador pensar que desconhecemos algo se não o soubermos definir explicitamente; na maior parte das vezes, as definições implícitas são perfeitamente adequadas. Contudo, faz parte do estudo sistemático em qualquer área, seja na filosofia ou na ciência, conseguir definir explicitamente os conceitos mais importantes e centrais da área em causa. Do modo como Platão descreve Sócrates, este parecia particularmente preocupado com o facto de os seus concidadãos serem incapazes de definir explicitamente alguns dos conceitos centrais da filosofia, como os de justiça e conhecimento, por exemplo. (Desidério Murcho)
democracia deliberativa
Tipo de democracia que dá ênfase à participação dos cidadãos e aos mecanismos racionais e discursivos de tomada de decisão, supostamente subalternizados pelos processos de decisão tradicionais da democracia representativa. Os seus defensores afirmam que é uma forma de aproximar os decisores dos cidadãos, de permitir a participação de minorias e a expressão de pontos de vista normalmente excluídos pelos processos de tomada de decisão maioritários, de respeito e esclarecimento mútuo e de obter consensos entre participantes livres e iguais. Os críticos, pelo contrário, afirmam que a democracia deliberativa é potencialmente destrutiva (porque o objectivo de alcançar o consenso torna praticamente impossível chegar a decisões, sobretudo em matérias urgentes) e utópica (porque pretende associar deliberação e participação de massas). (Álvaro Nunes)
democracia representativa
Forma de governo em que as pessoas elegem representantes que fazem e aplicam as leis. Se à representatividade se acrescentar a promoção das liberdades básicas dos cidadãos, a democracia representativa torna-se também liberal (ver liberalismo). Um argumento frequentemente apontado a seu favor é o de que constitui a forma de governo que melhor promove o bem-estar e a autonomia intelectual e moral dos cidadãos. Os críticos, por seu lado, tendem a ver nela a negação da própria democracia e apontam o perigo de conduzir a uma tirania electiva. Entre os muitos problemas que a democracia representativa enfrenta destacam-se os de saber como e quais representantes eleger de modo a garantir a eficácia governativa e como proteger as minorias derrotadas da “ditadura da maioria”. (Álvaro Nunes)
definiendum
Expressão latina que significa “a definir”; em definições do tipo “F é G” ou “F se, e só se, G” refere-se ao F. Por exemplo, ao definir conhecimento como crença verdadeira justificada, “conhecimento” é o definiendum. (Desidério Murcho)
definiens
Expressão latina que significa “o que define”; em definições do tipo “F é G” ou “F se, e só se, G” refere-se ao G. Por exemplo, ao definir conhecimento como crença verdadeira justificada, “crença verdadeira justificada” é o definiens. (Desidério Murcho)
deísmo
Há diversos tipos de deísmo, mas, em geral, trata-se de uma concepção acerca de Deus que assenta em pelo menos uma das seguintes teses: 1) Existe um Deus criador, mas uma vez criado o mundo, ele não tem qualquer intervenção no curso dos acontecimentos; 2) Existe um Deus criador, mas não existe qualquer espécie de revelação divina que nos diga o que é correcto ou incorrecto acerca da nossa conduta moral, bastando para isso consultar a razão humana; 3) Existe um ser supremo criador, mas esse ser não é o Deus revelado pelas religiões. Locke, Voltaire (1694–1778) e Rousseau (1712–1778) defenderam algumas formas de deísmo. (Aires Almeida)
deliberação
A consideração dos factores que tornam uma acção preferível a outras, tendo em conta a informação disponível acerca da realidade e as previsíveis consequências da nossa escolha. O instrumento privilegiado da deliberação é o raciocínio prático (ver razão prática), mediante o qual se avalia qual das várias acções possíveis melhor concretiza os nossos desejos e melhor se adequa às nossas crenças. Actualmente, a teoria da decisão constitui um suporte teórico indispensável para as deliberações dos juristas, dos gestores, dos médicos ou dos cientistas no seu trabalho, tendo conhecido um desenvolvimento assinalável no último século. (António Paulo Costa)
demarcação, critério de
Ver critério de demarcação.
demarcação, problema da
Ver critério de demarcação.
democracia
Sistema de governação do povo, pelo povo (democracia directa) ou seus representantes (democracia representativa), e para o povo. Platão defendeu que a democracia é irracional porque coloca o poder de decisão nas mãos da maioria da população, que muitas vezes não tem o conhecimento apropriado para tomar as melhores decisões. Outra crítica relacionada com esta é que a democracia, sem restrições, é apenas uma injusta ditadura da maioria. Finalmente, discute-se também se a democracia tem valor em si ou se tem valor apenas porque as suas consequências são melhores do que as de qualquer outra forma de governação. (Desidério Murcho)
demonstração
O mesmo que derivação.
denotação
1. A denotação de um nome próprio como “Aristóteles” é aquilo que o nome refere: o próprio Aristóteles, neste caso.
2. Aplicado a classes, o termo “denotação” é equivalente ao mais corrente “extensão”. Ver também conotação, referência. (Pedro Santos)
deontologia
Ver ética deontológica.
derivação
Uma forma de mostrar conclusivamente, passo a passo e de um ponto de vista exclusivamente sintáctico, que uma dada forma argumentativa é válida (ver sintaxe e forma lógica). Derivar uma conclusão de um conjunto de premissas é mostrar que a conclusão é uma consequência lógica das premissas em causa. Uma maneira de fazer isso é proceder passo a passo, procurando que cada passo seja de tal forma evidente que não possa esconder erros de raciocínio. Uma derivação é um dispositivo da lógica formal para o fazer de forma completamente rigorosa — e por isso é um modelo do que é pensar correctamente. Há diferentes estilos de derivações. Uma derivação simplificada tem o seguinte aspecto:
| 1. | R e não S | Premissa |
| 2. | Se P, então S | Premissa |
| 3. | Não S | 1, Eliminação da conjunção |
| 4. | Não P | 2, 3, modus tollens |
| 5. | R | 1, Eliminação da conjunção |
| 6. | R e não P | 4, 5, Introdução da conjunção |
A primeira coluna limita-se a numerar os passos; a segunda coluna apresenta as formas lógicas que são objecto do raciocínio; e a terceira coluna justifica cada um dos passos dados, apelando a regras válidas. As derivações são dispositivos sintácticos para determinar a validade de argumentos porque não fazem qualquer referência às condições de verdade (ver tabela de verdade) das premissas e conclusão, ao contrário do que acontece nos inspectores de circunstâncias, que determinam a validade em função das condições de verdade das premissas e conclusão em causa. (Desidério Murcho)
Descartes, René (1596–1650)
Filósofo, matemático e cientista francês. É considerado o pai da filosofia moderna. Abandonou os métodos que até então eram habituais da filosofia do continente europeu e que seguiam o estilo de Tomás de Aquino: no estudo de cada problema filosófico recorria-se à comparação das teorias dos filósofos do passado, sobretudo Aristóteles, e das doutrinas da Bíblia. Ao invés, Descartes enfrenta directamente os problemas da filosofia, sem comparar as teorias dos filósofos anteriores e sem atender às doutrinas da Bíblia. A sua formação científica diferencia-o também de muitos filósofos medievais, cuja formação era fundamentalmente teológica. Descartes era, contudo, um homem muito religioso e alega que o seu método filosófico lhe foi revelado em sonhos.
No Discurso do Método (1637), Descartes apresenta um resumo do seu pensamento filosófico, que mais tarde desenvolve nas Meditações sobre a Filosofia Primeira (1641). A preocupação central de Descartes é conseguir estabelecer um método seguro para a filosofia, que a coloque no mesmo caminho de sucesso que a ciência do seu tempo começava a percorrer. Como muitos filósofos do seu tempo, Descartes está igualmente preocupado com o cepticismo. A sua famosa dúvida metódica consiste em levar até às últimas consequências as dúvidas dos cépticos, convencido de que no fim haverá uma verdade da qual não será possível duvidar. Santo Agostinho já tinha proposto o mesmo método de refutação do cepticismo, mas Descartes entende que, com base no que restar depois da aplicação da dúvida metódica, será possível reconstruir os fundamentos de todo o conhecimento. Descartes costuma por isso ser visto como um fundacionalista (ver fundacionalismo) com respeito à epistemologia.
A verdade irrefutável e que nem os cépticos mais radicais poderiam recusar é a própria existência de quem duvida; daí a famosa expressão “Penso, logo existo" — isto é, posso duvidar de tudo, incluindo da realidade do mundo exterior, mas, para poder duvidar, tenho de existir, e por isso a minha própria existência é indubitável e evidente. Mas a minha existência não se pode confundir com a existência do meu corpo, do qual posso duvidar. E Descartes introduz assim o famoso e poderoso argumento dualista: se é possível que o meu corpo seja uma ilusão, mas é impossível que eu seja uma ilusão, então eu não sou o meu corpo. Com base na certeza de que o eu existe, Descartes procura então mostrar a existência de Deus e, com base na existência de Deus, a existência do mundo exterior. A obra de Descartes, sobretudo as Meditações, é um modelo da actividade filosófica genuína e constitui um bom ponto para começar o estudo da filosofia. (Desidério Murcho)
Blackburn, Simon, Pense, Cap. 1 (Lisboa: Gradiva, 2001).
Descartes, René, Discurso do Método (Lisboa: Sá da Costa, 1984).
Descartes, René, Meditações sobre a Filosofia Primeira (Coimbra: Almedina, 1985).
Kenny, Anthony, História Concisa da Filosofia Ocidental, Cap. 11 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 4 (Lisboa, Presença, 1989).
descritivo
Ver normativo e descritivo.
desejo
Estado mental em que um dado acontecimento, acção, objecto ou estado, é representado como atraente, agradável ou apetecível. Em filosofia da mente, atribui-se ao desejo (e à crença) um papel central na explicação da acção e do comportamento humano. Alguns filósofos, como Hume, defendem que o desejo é o “motor” da acção moral e que sem desejo esta não existiria. Ver intenção e ética. (António Paulo Costa)
desobediência civil
Forma de protesto em que se infringe deliberadamente a lei. A desobediência civil tem um carácter público e destina-se a combater uma injustiça, que por vezes reside na própria lei infringida. Por exemplo, pode-se praticar a desobediência civil infringindo leis de segregação racial de modo a alertar a opinião pública para a injustiça do racismo. Quem recorre à desobediência civil costuma ser escrupulosamente pacífico e estar disposto a sofrer as sanções jurídicas decorrentes da infracção à lei. Ver justiça. (Pedro Galvão)
determinismo
Na sua versão radical, é uma teoria que afirma que todos os estados ou acontecimentos do mundo são determinados por estados ou acontecimentos que lhes são anteriores, de acordo com as leis da natureza. Nesta versão, defende-se que, para qualquer acontecimento b, existe um acontecimento a anterior tal que é impossível que ocorra a sem que, consequentemente, ocorra b. Se esta versão mais radical for verdadeira, levanta-se o problema de saber se é compatível com o livre-arbítrio, isto é, se a acção humana pode ser concebida como genuinamente livre — os compatibilistas defendem que sim; os incompatibilistas, que não. O determinismo não deve ser confundido com o fatalismo, que é a doutrina segundo a qual nada do que fizermos agora terá eficácia causal. Além disso, nem todos os deterministas são radicais, existindo filósofos que defendem um determinismo moderado. Ver compatibilismo e incompatibilismo, libertismo e indeterminismo. (António Paulo Costa)
Deus
A ideia de Deus é o aspecto central de quase todas as religiões (exceptuando algumas versões do budismo), apesar de existirem diversas concepções de Deus. Para algumas religiões — cristianismo, judaísmo e islamismo — há um só Deus e por isso se chamam monoteístas. Mas há também religiões politeístas, de acordo com as quais não existe apenas um Deus, mas vários. A noção de Deus não é, contudo, exclusiva das religiões. Muitas pessoas, como sucede com os panteístas, acreditam que Deus é imanente ao mundo e às coisas que dele fazem parte, mas as principais religiões monoteístas concebem Deus como um ser transcendente. A concepção de Deus mais discutida em filosofia é a concepção teísta (ver teísmo), exposta nos grandes livros sagrados, como a Bíblia e o Corão, e consolidada e desenvolvida ao longo dos séculos pelos mais destacados representantes das grandes religiões ocidentais. Entre eles encontram-se filósofos como Santo Agostinho, Santo Anselmo (1033–1109) e Tomás de Aquino. O teísmo é a concepção de Deus discutida também por Descartes, Hume e Kant, entre muitos outros. O Deus teísta é um Deus criador do mundo, sumamente bom, todo-poderoso e infinitamente sábio. É também encarado por alguns teólogos como fonte de obrigações morais, ou mandamentos, que determinam o que é moralmente bom e moralmente mau. São muito discutidos em filosofia da religião os argumentos a favor da existência de Deus, havendo três grandes linhas de argumentação: o argumento ontológico, o argumento cosmológico e o argumento do desígnio. Ver também problema do mal. (Aires Almeida)
dever
O dever moral de um agente é aquilo que ele tem a obrigação de fazer. A noção de dever é central numa ética deontológica, como a de Kant. Na ética de Kant, distinguem-se os deveres perfeitos dos imperfeitos: os primeiros, como o dever de não mentir, têm de ser respeitados em quaisquer circunstâncias; os segundos, como o dever de ajudar os outros, não constituem uma obrigação permanente. Isto significa que, embora devamos fazer algo para ajudar os outros, não temos de estar sempre empenhados nisso nem podemos desrespeitar quaisquer deveres perfeitos (por exemplo, mentir a alguém) para prestar ajuda. Kant distinguiu também dois tipos de actos que estão de acordo com o dever: os que são realizados apenas por dever e os que estão em mera conformidade com o dever. Neste últimos o agente faz o que deve, mas por motivos egoístas ou por compaixão; Kant sustenta que só os primeiros, que resultam do respeito puramente racional pelo dever, têm valor moral. Ver direitos, máxima, vontade boa. (Pedro Galvão)
devir
Falar do devir das coisas é uma forma de falar da mudança ou fluxo das coisas. Um tema comum na filosofia da antiguidade grega era saber se haveria alguma estabilidade além da mudança constante que se observa na natureza, pois achava-se que só a descoberta dessa constância poderia ajudar a compreender a própria mudança. Heraclito (cerca de 535-475 a. C.) e Parménides (séc. V a. C.) representavam na antiguidade dois filósofos opostos quanto ao papel da mudança. Heraclito ficou associado à ideia de que tudo está em mudança, e Parménides à ideia contrária de que a mudança é apenas aparente, sendo a realidade última imutável. Contudo, a verdadeira oposição entre estes filósofos era mais subtil. Ambos concordavam que além da mudança aparente havia uma realidade imutável, a que Heraclito chamava “logos" (razão). A diferença residia no facto de Heraclito pensar que a própria mudança era apenas uma faceta particular do imutável, ao passo que Parménides entendia que a mudança era uma completa ilusão. (Desidério Murcho)
dialéctica
Originariamente, a arte do diálogo e da discussão. Em Sócrates é o processo que permite, por perguntas e respostas, refutar (ver refutação) os oponentes expondo as contradições (ver contradição) e as dificuldades das suas posições. Para Platão, a dialéctica é o processo que permite remontar, a partir de hipóteses, de ideia em ideia até à ideia de Bem. Aristóteles considera a dialéctica o estudo dos raciocínios que, ao contrário dos demonstrativos (ver demonstração), partem de premissas (ver premissas) somente prováveis. Kant chama dialécticos a todos os raciocínios ilusórios e define a dialéctica como uma lógica da ilusão. A “Dialéctica Transcendental” é o estudo das ilusões (paralogismos e antinomias) em que a razão cai quando aplicada para além dos limites de toda a experiência possível. Os idealistas alemães (ver idealismo) vêem na dialéctica uma noção triádica, constituída de tese, antítese e síntese, que Hegel pensa constituir o processo histórico necessário ao desenvolvimento do espírito e Marx da matéria. Usa-se também a expressão “dialéctica argumentativa” para referir o modo como se desenvolve a troca de argumentos numa discussão. (Álvaro Nunes)
dianoia
Termo grego que refere um tipo de conhecimento cujo objecto são questões matemáticas e técnicas, e que Platão considera inferior à noesis. O termo é também usado de forma mais geral unicamente para referir a expressão do pensamento. (Desidério Murcho)
dilema
1. Em lógica, um dilema é um argumento com a seguinte forma: P ou Q; se P, então R; se Q, então R; logo, R. Por exemplo: “O prazer ou a felicidade é o bem maior; se for o prazer, temos de procurar eliminar o sofrimento; se for a felicidade, temos igualmente de eliminar o sofrimento; logo, em qualquer dos casos, temos de eliminar o sofrimento”. Chama-se “dilema construtivo simples” a este dilema e é dos mais comuns. Menos habituais são os dilemas construtivos complexos (P ou Q; se P, então R; se Q, então S; logo, R ou S). Chamam-se “dilemas destrutivos” quando a conclusão é negativa e não afirmativa. Ver falso dilema.
2. Em geral, um dilema é uma situação na qual estamos perante duas alternativas, temos de escolher uma delas e nenhuma delas é agradável. (Desidério Murcho)
dilema de Êutifron
Dilema apresentado pela primeira vez por Platão no diálogo Êutifron. Este dilema proporciona um argumento poderoso contra a teoria dos mandamentos divinos. Podemos introduzi-lo através desta pergunta, onde x é um acto como matar, roubar ou mentir: x é errado porque Deus julga que x é errado ou Deus julga que x é errado porque x é errado? Se optarmos pela segunda hipótese, temos de rejeitar a teoria dos mandamentos divinos, porque estamos a presumir, afinal, que certas coisas são erradas independentemente do que Deus pensa sobre elas. Se optarmos pela primeira hipótese, temos de concluir que, se Deus considerasse bom fazer coisas como matar, roubar ou mentir, então seria bom fazer essas coisas. Esta hipótese, no entanto, faz da ética um conjunto de convenções tão arbitrárias como a de que devemos conduzir pela direita e não pela esquerda. (Pedro Galvão)
dilema de Hume
Um dilema clássico acerca da liberdade e da responsabilidade. O dilema de Hume, ou dilema do determinismo, pode ser esquematizado da seguinte forma:
1.ª premissa — Ou o determinismo é verdadeiro, ou é falso;
2.ª premissa — Se for verdadeiro, então não somos livres;
3.ª premissa — Se for falso, as nossas acções são aleatórias e, portanto, também não somos livres.
Conclusão — Em qualquer caso, não somos livres.
O desafio posto por este argumento é o de nos instar a encontrar uma alternativa à determinação completa ou à aleatoriedade total das acções, que têm como consequência a negação da responsabilidade humana. (António Paulo Costa)
direitos
Um direito é uma pretensão legítima a uma coisa. Se as pessoas têm direitos morais, então é errado privá-las daquilo a que elas têm direito para benefício dos outros. Por exemplo, se as pessoas têm o direito à vida, não se pode assassinar uma pessoa para salvar outras. Os direitos impõem limites àquilo que é permissível fazer em nome da felicidade geral ou do bem comum (ver utilitarismo), e por isso costumam ser reconhecidos pelos que defendem uma ética deontológica. Não se deve confundir os direitos legais com os direitos morais. Para saber se os animais têm direitos legais, basta consultar a legislação; para saber se têm direitos morais, é preciso investigar as características que conferem direitos a uma entidade e determinar se os animais possuem essas características. (Pedro Galvão)
discriminação positiva
Quando se recorre à discriminação positiva dá-se tratamento preferencial a membros de grupos sociais desfavorecidos. Em alguns países a discriminação positiva é usada com muita frequência no ensino e no emprego. Por exemplo, num país em que as mulheres vivem oprimidas, uma universidade pode recorrer à discriminação positiva reservando um certo número de vagas para as mulheres. Com esta medida controversa, procura-se promover a igualdade ou compensar as vítimas de desigualdades injustas. Ver justiça. (Pedro Galvão)
discursivo
O que se refere ao discurso, entendido como qualquer segmento de linguagem em que se articulam várias frases, como conversas faladas ou escritas, textos, troca de argumentos, narrativas, etc. Para a análise e compreensão do discurso intervêm aspectos como a relação de implicação entre aquilo que as frases exprimem, os pressupostos do que é afirmado, a força argumentativa, os aspectos contextuais, etc., que são estudados por disciplinas como a linguística, a lógica, a filosofia da linguagem e, em muitos casos, também a sociologia, a psicologia e a retórica. Dizer que a filosofia tem uma dimensão discursiva é dizer que utiliza instrumentos lógicos e linguísticos. (Aires Almeida)
disjunção (∨)
Qualquer afirmação da forma “P ou Q”, como “Platão, ou Sócrates, era grego”. Uma disjunção é verdadeira se, e só se, pelo menos uma das proposições que a constituem for verdadeira. Isto significa que a disjunção só será falsa se ambas as proposições, P e Q, forem falsas. Mas este é apenas um dos tipos de disjunção, a que se chama inclusiva. Há também a chamada disjunção exclusiva, que se distingue da anterior pelo seguinte: é falsa caso ambas as proposições, P e Q, sejam verdadeiras; por exemplo, em muitos casos a seguinte afirmação é, infelizmente, uma disjunção exclusiva: “Estudo ou vou ao cinema”. (Aires Almeida)
divisão, falácia da
Ver falácia da divisão.
dogma
Uma afirmação ou teoria cujo partidário se recusa a discutir e para a qual não apresenta quaisquer razões sólidas. Por exemplo: quem defende que os animais não têm direitos porque são animais, e se recusa a discutir o tema, está a afirmar um dogma. Neste sentido, a filosofia, a ciência e as artes opõem-se ao pensamento dogmático dado que tendem a favorecer a diversidade e a discussão aberta. (Desidério Murcho)
doxa
Termo grego que significa “crença”, “opinião”, ou ainda “o que se diz”. Platão foi um dos primeiros filósofos a colocar, no diálogo Teeteto, o problema da distinção entre a doxa e a episteme, isto é, entre opinião ou crença e conhecimento. Ver epistemologia.
dualismo e monismo
Uma tese dualista defende que, num certo domínio, existem dois géneros de coisas diferentes e irredutíveis; uma tese monista, pelo contrário, defende que nesse domínio existe um só género de coisas. Usa-se estes termos principalmente em filosofia da mente. Filósofos como Platão, Aristóteles, Descartes e Kant defenderam a tese clássica do dualismo entre o corpo ea alma, segundo a qual o corpo e a alma têm naturezas essencialmente distintas. Esta tese enfrenta o problema de explicar as relações entre o físico e o mental, em especial a causalidade que ocorre entre ambos. Pelo contrário, o monismo defende que não há, a este respeito, uma genuína dualidade entre o corpo e a alma. O idealismo e o fisicismo são as duas teorias monistas mais importantes. (António Paulo Costa)
dúvida
Duvida-se de uma afirmação ou argumento quando se questiona a sua verdade ou solidez. Ver cepticismo e Descartes. (Desidério Murcho)
dúvida metódica
Estratégia proposta por Descartes para procurar aquele conhecimento seguro que nenhuma dúvida céptica poderia pôr em causa. A ideia é duvidar de tudo o que seja possível duvidar até encontrar algo de que não possamos duvidar; Descartes defende que podemos duvidar de tudo, mas não da nossa própria existência. (Desidério Murcho)
E
egoísmo ético
Perspectiva normativa (ver normativo e descritivo) segundo a qual qualquer agente humano deve agir sempre e unicamente em função daquilo que é efectivamente melhor para si. (Pedro Galvão)
egoísmo psicológico
Perspectiva descritiva (ver normativo e descritivo) segundo a qual qualquer agente humano age sempre tendo em vista apenas aquilo que julga ser melhor para si. Assim, qualquer acto aparentemente altruísta (por exemplo, arriscar a própria vida para salvar outra pessoa) esconde um motivo egoísta (por exemplo, parecer corajoso aos olhos dos outros). (Pedro Galvão)
eidos
Termo grego que significa “forma” ou “ideia”. Platão considerava que as Formas ou Ideias eram imutáveis, imateriais e não podiam ser percepcionadas pelos sentidos, mas eram a realidade última, sendo as coisas quotidianas apenas uma pálida semelhança das Formas. (Desidério Murcho)
elenchos
Termo grego que significa “interrogatório”, e que costuma ser usado para referir o método usado por Sócrates, que consistia em fazer perguntas aos seus interlocutores com o objectivo de descobrir verdades importantes acerca de conceitos filosóficos centrais, como justiça, bem e verdade. (Desidério Murcho)
emoção estética
O tipo de sentimento que, segundo alguns filósofos, só as obras de arte conseguem despertar em nós e que se distingue dos sentimentos provocados por quaisquer outros objectos. De acordo com esses filósofos, o que nos permite identificar uma verdadeira obra de arte é o facto de ela provocar em nós um tipo peculiar de emoção, a emoção estética. O filósofo e crítico de arte Clive Bell (1881–1964) considera que há nas obras de arte, e só nelas, uma certa propriedade que provoca em nós emoções estéticas. A essa propriedade dá o nome de forma significante. Nem todos os filósofos admitem a existência de emoções estéticas. (Aires Almeida)
emotivismo
Teoria metaética segundo a qual não há factos morais e, portanto, os juízos morais não têm valor de verdade. Para o emotivista, ao fazer um juízo moral estamos apenas a exprimir certos sentimentos ou atitudes. Isto significa que quando uma pessoa diz, por exemplo, que o aborto é errado, está só a exprimir uma atitude pessoal de reprovação relativamente ao aborto — não está a fazer uma afirmação sobre o aborto que possa ser avaliada como verdadeira ou falsa. Tal como o subjectivismo moral, o emotivismo nega a objectividade da ética. Ver objectivismo e subjectivismo. (Pedro Galvão)
empírico
Diz-se do que se refere à experiência sensível. Assim, uma afirmação é empírica se descrever ou de algum modo estiver relacionada com a descrição de um estado de coisas de que temos experiência e puder ser confirmada ou falsificada pela experiência sensível. E o mesmo se aplica em relação às nossas crenças. Ao afirmar que há seres inteligentes extraterrestres estamos a defender uma tese empírica; ao afirmar que Lisboa é maior do que Faro estamos a exprimir uma crença empírica. Isto contrasta com teses ou crenças não empíricas (isto é, conceptuais), como a tese de que 30 + 60 = 90, ou a crença de que o vermelho é uma cor (o que é diferente da crença de que um dado objecto é vermelho). Podemos ainda falar de qualidades empíricas quando dizemos, por exemplo, que determinado objecto é azul. Neste caso trata-se de uma qualidade empírica porque referimos uma característica que pode ser directamente observada, enquanto que as qualidades teóricas são inferidas (ver inferência). Ver também a priori e a posteriori e empirismo. (Aires Almeida)
empirismo
Perspectiva filosófica de acordo com a qual todo o nosso conhecimento substancial deriva da experiência e das impressões colhidas pelos cinco sentidos (ver a priori e a posteriori). O empirismo divide-se, em geral, em duas posições. A posição segundo a qual todo o conhecimento deriva da experiência, não havendo espaço para o conhecimento a priori (esta é a posição empirista radical); e a posição segundo a qual, apesar de todo o nosso conhecimento substancial derivar da experiência, existe conhecimento a priori, só que este não é substancial, nada nos diz acerca do mundo exprimindo meras relações entre os conceitos (esta é a posição empirista moderada). Um dos primeiros grandes filósofos empiristas foi o inglês do séc. XVII John Locke. Este defendeu que a nossa mente se compara a uma folha de papel em branco (ou a uma tábua rasa, como dizia Aristóteles) na qual os nossos sentidos vão deixando registadas as impressões colhidas do exterior. A mente era vista como uma espécie de recipiente que se vai enchendo à medida que o contacto com o mundo à nossa volta o permite, mas incapaz de ter uma intervenção activa que não seja a interpretação e manipulação dos dados sensíveis. O desrespeito pelos dados sensíveis é que está, segundo o empirista, na origem das interpretações abusivas em que se apoiam as nossas crenças falsas. O empirismo opõe-se, pois, ao racionalismo, o qual defende que podemos obter conhecimento a priori substancial acerca do mundo. O filósofo escocês do séc. XVIII David Hume enfrentou, sempre numa perspectiva empirista, algumas das dificuldades apontadas pelos racionalistas, acabando por tirar a conclusão céptica (ver cepticismo) de que era impossível basear na experiência ideias tão importantes para a ciência como as de causalidade e de universalidade (ver universais). Os ingleses Stuart Mill (séc. XIX), o alemão Rudof Carnap e o filósofo americano W. V. Quine estes já no séc. XX, são alguns dos mais destacados empiristas. São duas as grandes dificuldades que qualquer teoria empirista enfrenta, explicar a forte intuição de que temos conhecimento a priori substancial, e explicar a forte intuição de que existem verdades necessárias. Ver também coerentismo, fundacionalismo, indução, pragmatismo, verificacionismo. (Aires Almeida)
Blackburn, Simon, Pense: Uma Introdução à Filosofia, capítulo 1 (Lisboa: Gradiva, 2001).
Kenny, Anthony, História Concisa da Filosofia Ocidental, capítulos 12 e 14 (Lisboa: Temas e Debates, 1999).
Nagel, Thomas, O Que Quer Dizer Tudo Isto?, capítulo 2 (Lisboa: Gradiva, 1995).
Russell, Bertrand, Os Problemas da Filosofia, capítulos V-X (Coimbra: Almedina, 2001).
entimema
Um argumento com pelo menos uma premissa não explicitada. Chama-se por vezes “premissa implícita" à premissa não formulada. Na argumentação quotidiana estamos habituados a omitir premissas óbvias. A premissa implícita do argumento “O António devia ser despedido porque roubou dinheiros públicos” é razoavelmente clara: “Todas as pessoas que roubam dinheiros públicos devem ser despedidas”. Mas qual será a premissa implícita do argumento “A droga deve ser proibida porque provoca a morte"? Se a premissa implícita for o princípio geral de que tudo o que provoca a morte deve ser proibido, o seu locutor está obrigado a aceitar que a condução de automóveis deve também ser proibida, o que o autor do argumento original pode não estar disposto a aceitar. Descobrir as premissas implícitas das nossas ideias ou das ideias dos filósofos é uma parte importante do trabalho filosófico. (Desidério Murcho)
enunciado
Termo utilizado correntemente com o significado de frase, ou mais especificamente, de frase declarativa com sentido, mas que na lógica e na filosofia significa antes aquilo que é expresso por intermédio de uma frase declarativa com sentido. Ver proposição. (Álvaro Nunes)
epicurismo
Juntamente com o estoicismo e o cepticismo, uma das três grandes filosofias do período helenístico. Tem origem na filosofia de Epicuro (341–271 a. C), filósofo grego que em 306 fundou em Atenas uma escola chamada “Jardim”. O epicurismo retoma e desenvolve o atomismo de Leucipo e Demócrito, defendendo que os únicos existentes per se são os corpos, constituídos por átomos, e o espaço vazio, ambos infinitos. O universo é eterno e infinito e o nosso mundo é apenas um entre muitos. O prazer é o único bem e o objectivo natural do ser humano, ao qual todos os outros se subordinam. O sofrimento é o único mal e não existe qualquer estado intermédio. O nosso objectivo principal é minimizar o sofrimento, o que se consegue através de um modo de vida simples e do estudo da física, o qual elimina as duas principais fontes de angústia, o receio dos deuses e da morte, e permite alcançar um estado de tranquilidade ou imperturbabilidade (ataraxia), que constitui a forma de felicidade mais elevada e o objectivo correcto da vida. Ver hedonismo, mal moral, mal natural. (Álvaro Nunes)
epifenómeno
Um fenómeno que não tem poderes causais no que respeita a um dado processo, sendo muitas vezes apenas um subproduto do mesmo. Por exemplo, o fumo que vemos e o ruído que ouvimos de um comboio em movimento são causados pelo motor do comboio mas não causam eles o movimento do comboio. Se as propriedades mentais forem epifenomenais, então não podem causar as nossas acções. Esta é a doutrina central do epifenomenalismo. O conceito é importante em filosofia da ciência, filosofia da mente e filosofia da psicologia. (Miguel Amen)
episteme
Termo grego que significa “conhecimento” e de onde deriva a palavra “epistemologia”. Aristóteles usava o termo no sentido de conhecimento sistemático racional, a que hoje chamamos “ciência”, mas que para ele incluía a filosofia. (Desidério Murcho)
epistemologia
A disciplina tradicional da filosofia, também conhecida por teoria do conhecimento, que trata de problemas como “o que é o conhecimento?”, “o que podemos conhecer?”, “qual é a origem do conhecimento?”, “como justificamos as nossas crenças?”, envolvendo um conjunto de noções relacionadas entre si, como “conhecer”, “perceber”, “prova”, “crença”, “certeza”, “justificação” e “confirmação”, entre outras. O nome deriva de epistêmê, termo do antigo grego que significa conhecimento. A esse termo opunha-se o termo doxa, que significa opinião. Isto porque, como Platão começou por sublinhar, não é possível conhecer falsidades, sendo contudo possível — e até frequente — ter opiniões falsas. Assim, um dos problemas que desde logo se coloca é o de saber como se alcança o conhecimento e se evita a mera opinião. A célebre teoria das ideias de Platão continha uma resposta para esse problema. Para Platão, só através de um processo racional de afastamento das impressões sensíveis somos conduzidos à contemplação das Ideias perfeitas, de que os objectos captados pelos nossos sentidos são simples cópias imperfeitas. É nas Ideias que reside a verdade, pelo que o chamado “conhecimento sensível” não deve, em rigor, ser considerado conhecimento. A discussão acerca do papel dos sentidos na formação do conhecimento e na justificação das nossas crenças acabou por dar lugar a duas grandes doutrinas epistemológicas rivais: o empirismo e o racionalismo. Empiristas como os britânicos Locke, Hume e Berkeley defendem que todo o conhecimento substancial provém da experiência sensível, enquanto os racionalistas, como o francês Descartes e o alemão Leibniz, consideram que o conhecimento, se correctamente entendido, deve exibir as marcas da universalidade (ver universal) e da necessidade (ver necessário), características que de modo algum dependem da experiência. Assim, para os racionalistas nem todo o conhecimento deriva da experiência sensível. Kant, procurou determinar com exactidão como se constitui o conhecimento, concluindo que este depende tanto da matéria fornecida pelos sentidos como das formas a priori do pensamento a que os dados sensíveis têm de se submeter. Kant opõe-se assim tanto ao empirismo como ao racionalismo tradicional.
A justificação das nossas crenças é outro dos problemas epistemológicos que têm gerado importantes debates. Há filósofos que defendem que por muito boas que sejam, as nossas justificações nunca conseguem ser inteiramente satisfatórias, vendo-nos assim permanentemente confrontados com dúvidas insuperáveis. Este problema é também conhecido por “problema do cepticismo”, uma vez que os cépticos acabam por concluir, aparentemente de forma justificada, que o conhecimento não é possível. No sentido de evitar o cepticismo, muitos filósofos procuraram um fundamento para o conhecimento, isto é, um reduzido número de certezas inabaláveis a partir das quais se estrutura todo o nosso sistema de crenças. Essas certezas tanto podem pertencer ao domínio da razão como da experiência, consoante as inclinações racionalistas ou empiristas do filósofo. A este ponto de vista chama-se fundacionalismo, e Descartes constitui um dos exemplos mais conhecidos. Mas há também quem não aceite qualquer tipo de fundamento último para o conhecimento, sem contudo aderir ao cepticismo. É o caso dos defensores do coerentismo, para quem as nossas crenças se apoiam mutuamente umas nas outras sem precisarem que uma delas sustente as restantes. À maneira de uma rede ou das inúmeras peças de madeira de que é feito um barco, permitindo-lhe flutuar no mar sem se afundar — esta é a metáfora de Otto Neurath (1882–1945) —, o importante é que as crenças sejam coerentes entre si.
Mais directamente ligado ao que se passa com a ciência, embora não só, há o chamado problema da indução, a propósito do qual se discute se o tipo de justificação baseado em inferências indutivas é ou não aceitável. Podemos ainda encontrar problemas de epistemologia da religião, tratando-se aí da justificação das crenças religiosas; epistemologia da matemática, etc. (Aires Almeida)
Blackburn, Simon, Pense, Capítulo 1 (Lisboa: Gradiva, 2001).
Dancy, Jonnathan, Epistemologia Contemporânea (Lisboa: Edições 70, 1990).
Nagel, Thomas, O Que Quer Dizer Tudo Isto?, Capítulo 2 (Lisboa: Gradiva, 1995).
Russell, Bertrand, Os Problemas da Filosofia (Coimbra: Almedina, 2001).
Warburton, Nigel, Elementos Básicos de Filosofia, Capítulo 4 (Lisboa: Gradiva, 1998).
epochê
Termo grego que refere a suspensão da crença. O termo era usado pelos cépticos da Antiguidade Grega, como Pirro de Élis (c. 365-275 a. C.), o fundador do cepticismo grego, para referir o estado de não comprometimento por ele defendido perante teses ou teorias opostas; assim, perante a questão de saber se Deus existe ou não, Pirro defenderia a suspensão da crença ou epochê em relação a ambas as teses. O mesmo termo foi usado já no séc. XX por Edmund Husserl (1859–1938), o fundador da fenomenologia, para referir o acto de “pôr entre parênteses” as nossas crenças de senso comum, nomeadamente a de que o mundo exterior existe, adoptando uma postura mais reflectida e genuinamente filosófica. (Desidério Murcho)
equidade
A noção de equidade exprime a intuição moral básica de que todos os seres humanos merecem, à partida, igual consideração. Isto significa que o bem-estar de qualquer ser humano, independentemente das suas características e condição, tem, à partida, a mesma importância que o bem-estar de qualquer outro ser humano. Ver também Rawls, John. (Faustino Vaz)
equivalência
Duas afirmações são equivalentes se se implicam mutuamente (ver implicação). Há portanto tantos tipos de equivalência quantos os tipos admitidos de implicação. Por exemplo, a equivalência material entre duas afirmações P e Q ocorre quando elas se implicam materialmente entre si, isto é, quando não se tem que P é verdadeira e Q falsa nem vice-versa (ou seja, quando P e Q têm o mesmo valor de verdade); neste caso, é o mesmo que bicondicional. Um tipo de equivalência mais forte (e mais próximo do uso corrente do termo) verifica-se quando duas afirmações são logicamente equivalentes, caso em que têm necessariamente o mesmo valor de verdade (ver necessário e contingente). (Pedro Santos)
eros
Termo grego que significa “amor erótico”. Na Antiguidade Grega, os filósofos contrastavam o amor erótico com a amizade entre amigos, a que chamavam philia e de onde deriva o termo português “filial”. Mais tarde, os filósofos cristãos opunham o amor erótico ao amor cristão pelo próximo (agapê). (Desidério Murcho)
escolástica
O termo “escolástica” significa, literalmente, a filosofia “da escola”, isto é, a filosofia que se praticou nas universidades europeias medievais, fundadas no século XIII, em particular as de Paris e Oxford, embora se inclua na escolástica os “mestres de dialéctica" (ver Dialéctica) anteriores como Abelardo e Pedro Lombardo (1095–1160). A escolástica caracterizou-se por traduzir, estudar e comentar as obras de Aristóteles, e por integrá-las na teologia cristã, mas não se limitou a isso, pois os filósofos escolásticos também discutiram e defenderam teorias originais em lógica, metafísica, filosofia da linguagem e epistemologia. Uma das inovações importantes da filosofia escolástica foi a prática das disputas, em que os alunos tinham de defender uma dada tese ou a sua contrária, pondo à prova as aptidões argumentativas (ver argumento). Entre os principais autores deste período estão Tomás de Aquino, Duns Escoto e Guilherme de Ockham. As preocupações fundamentais destes autores incluíam, na epistemologia, a relação entre a razão e a fé, e, na metafísica, o chamado problema dos universais, que opõe duas grandes doutrinas, o nominalismo e o realismo, e é ainda um dos debates fundamentais da metafísica contemporânea. (Vítor Guerreiro)
esse est percipi
Expressão latina que significa “ser é ser percepcionado”. Ver Berkeley.
essência
A essência de uma coisa é uma propriedade essencial individuadora dessa coisa. Ou seja, é uma propriedade que uma coisa tem, que não poderia deixar de ter e que a distingue de todas as outras coisas. Por exemplo, a essência da água é ser H2O. Não se deve confundir essência com propriedade essencial, pois nem todas as propriedades essenciais são individuadoras. Por exemplo, o código genético de um organismo é uma propriedade essencial desse organismo; mas não é uma propriedade que o distingue de outros organismos que podem ter o mesmíssimo código genético — os seus irmãos gémeos. (Desidério Murcho)
essencialista, definição
Ver definição essencialista.
estado
A noção moderna de estado surgiu com Maquiavel e Hobbes, e inclui os seguintes aspectos: a) uma população formada por membros socialmente relacionados entre si; b) um território; c) um governo que tem o poder de estabelecer leis e usar a coerção, de modo a regular o comportamento dos indivíduos dentro de certos limites; d) independência e reconhecimento político de outros estados. Um debate importante em filosofia política é o de saber qual deve ser o papel do estado na regulação da vida dos indivíduos. Filósofos como John Locke e Robert Nozick (1938-2002) defendem que o papel do estado deve ser muito limitado, de modo a não pôr em causa a liberdade individual (ver liberalismo). John Rawls, por sua vez, acha que o estado deve intervir para garantir uma maior justiça social. Os anarquistas defendem que a existência do estado não se justifica. (Aires Almeida)
estética
Uma das disciplinas tradicionais da filosofia, que aborda um conjunto de problemas e conceitos por vezes muito diferentes entre si. A estética começou por ser sobretudo uma teoria do belo, depois passou a ser entendida como teoria do gosto e nos nossos dias é predominantemente identificada com a filosofia da arte. Há fortes razões para considerar que estas três formas de encarar a estética não são apenas diferentes maneiras de abordar os mesmos problemas. É certo que gostamos de coisas belas que também são arte, mas não deixa de ser verdade que as coisas que consideramos belas, aquelas de que gostamos e as que são arte, formam conjuntos distintos. Afinal, até é banal gostarmos de coisas que não são belas e muito menos arte; assim como podemos nomear obras de arte de que não gostamos nem consideramos belas.
Enquanto teoria do belo, a estética defronta-se com problemas como “O que é o belo?” e “Como chegamos a saber o que é o belo?”. Estas são perguntas que já Platão colocava no séc. IV A.C e que só indirectamente diziam respeito à arte, pois a arte consistia, para ele, na imitação das coisas belas. Razão pela qual Platão tinha uma opinião desfavorável à arte, ao contrário do seu contemporâneo Aristóteles, para quem a imitação de coisas belas tinha os seus próprios méritos.
Já para os filósofos do séc. XVIII, como Hume e Kant, é no campo da subjectividade que se encontra a resposta para o problema do belo. A estética transformou-se, assim, em teoria do gosto, cujo problema central passou a ser o de saber como justificamos os nossos gostos. O subjectivismo estético é a doutrina defendida por estes dois filósofos, embora com tonalidades diferentes. A doutrina rival é o objectivismo estético e é bem representado pelo filósofo americano contemporâneo Monroe Beardsley (1915-85), para quem o belo não depende dos gostos pessoais, mas da existência de certas características nas próprias coisas.
Finalmente, as revoluções artísticas dos dois últimos séculos, ao alargar de tal modo o universo de objectos que passaram a ser catalogados como arte, acabaram por despertar nos filósofos vários problemas que se tornaram o centro das disputas estéticas. É o caso dos problemas de filosofia da arte como “O que é arte?” e “Qual o valor da arte?”, entre outros. Quanto ao problema da definição de arte, há três tipos de teorias: as essencialistas — teorias da representação, da expressão e formalista —, as não-essencialistas — teorias institucionais, de filósofos como o americano George Dickie (n. 1936) — e as que, inspiradas no filósofo austríaco Wittgenstein, consideram ser impossível definir “arte”. Relativamente ao problema do valor da arte, encontramos dois tipos de teorias: as que defendem que a arte tem valor em si — teorias da arte pela arte, tendo Oscar Wilde (1854–1900) como defensor mais conhecido — e as que defendem que a arte tem valor porque tem uma função (teorias funcionalistas), seja ela social, moral, terapêutica, lúdica ou cognitiva. A função cognitiva é das mais discutidas e o filósofo americano contemporâneo Nelson Goodman é um dos seus mais importantes defensores, considerando a arte uma importante forma de conhecimento. Ver também cognitivismo estético, esteticismo, funcionalismo estético. (Aires Almeida)
Graham, Gordon, Filosofia das Artes (Lisboa: Edições 70, 2001).
Warburton, Nigel, Elementos Básicos de Filosofia, capítulo 7 (Lisboa: Gradiva, 1998).
Townsend, Dabney, Introdução à Estética (Lisboa: Edições 70, 2002).
esteticismo
Doutrina segundo a qual a arte tem valor em si e não porque cumpre alguma função ou propósito exterior a si. O esteticismo opõe-se às teorias funcionalistas (ver funcionalismo estético), de acordo com as quais a arte tem uma função, seja ela moral, política, lúdica, cognitiva ou outra qualquer. Oscar Wilde (1854–1900), um dos mais destacados defensores do esteticismo, considera que a arte se eleva acima de tudo o resto precisamente porque é inútil. Isto não significa que não existam obras de arte que são criadas tendo em vista certos objectivos (é o caso das obras de arte religiosa e da arte de intervenção), mas o seu valor não depende de tais objectivos serem ou não alcançados. O que torna uma obra de arte bela ou digna de admiração são as suas características internas e tudo o mais constitui, em muitos casos, um defeito que só prejudica a própria obra. O esteticismo identifica-se em grande parte com a conhecida teoria da arte pela arte, que surgiu em França com figuras como o poeta Baudelaire (1821–67). Ver também formalismo estético. (Aires Almeida)
estoicismo
Corrente filosófica fundada por Zenão de Cítio (332–264 a.C.) no terceiro séc. antes da era cristã e que está associada a pensadores como Séneca (4 a.C.-65 d.C.), Epicteto (50–138 d. C.) e o imperador romano Marco Aurélio (121–180 d. C.). Para os estóicos, a filosofia tem como finalidade essencial formar o homem sábio. A Sabedoria consiste na prática da virtude, em viver de acordo com a natureza ou a ordem racional (logos) do universo. O logos é a divindade imanente ao mundo e tudo governa necessariamente. O Sábio, com serenidade e autodomínio, compreende o carácter necessário do que acontece. O estoicismo desenvolveu a primeira moral de tipo universal fundada na igualdade de princípio de todos os homens (considerados cidadãos do mundo — cosmopolitismo). Em lógica devemos a Crisipo (279-206 a.C.) a análise de enunciados compostos tais como condicionais e disjuntivos e a identificação das formas padrão de raciocínio que vieram a ser conhecidas pelo nome de modus ponens e modus tollens. (Luís Rodrigues)
ética
Disciplina tradicional da filosofia, também conhecida por filosofia moral, que enfrenta o problema de saber como devemos viver.
A área da ética que lida com este problema da forma mais directa é a ética normativa. A ética normativa ocupa-se em grande medida de dois problemas mais específicos: 1) O que é agir de uma forma moralmente acertada? 2) O que torna boa ou valiosa a vida de uma pessoa? Ao tentar responder a esta perguntas, os filósofos propõem, respectivamente, teorias da obrigação e teorias do valor. As primeiras só floresceram a partir do séc. XVIII e exprimem-se em princípios, como o imperativo categórico de Kant, que nos proporcionam um padrão para determinar aquilo que é moralmente obrigatório ou permissível fazer. Há dois tipos fundamentais de teoria da obrigação. Quem, como Mill, Hare ou Singer, defende uma ética consequencialista, pensa que para determinar o que devemos ou podemos fazer precisamos apenas de avaliar as consequências dos nossos actos: a melhor opção ética é sempre aquela que dará origem aos melhores resultados. Quem, como Kant, defende uma ética deontológica, julga que a nossa prioridade enquanto agentes morais é evitar realizar certos tipos de actos — ou, como dizem alguns deontologistas, respeitar certos direitos.
O interesse pelas teorias do valor remonta à Antiguidade. Filósofos como Aristóteles, bem como os representantes do epicurismo, do estoicismo e de outras escolas, esforçaram-se por compreender o que é ter uma vida boa. Grande parte do debate sobre esta questão constitui-se a partir de duas perspectivas contrárias: enquanto alguns autores defendem que temos uma vida boa na medida em que conseguimos satisfazer os nossos desejos, outros pensam que aquilo que torna a nossa vida boa é a presença de certos bens que têm valor independentemente de serem desejados, como o conhecimento, a amizade e a apreciação da beleza. Entre os filósofos que subscrevem esta segunda perspectiva, encontramos os defensores do hedonismo, que pensam que na verdade há um único bem fundamental: o prazer.
O desenvolvimento da ética normativa conduziu, há algumas décadas, ao aparecimento de outra área da filosofia moral — a ética aplicada. Nesta área discute-se o que é obrigatório ou permissível fazer pensando em certos problemas morais concretos que dividem as pessoas. Discute-se, por exemplo, em que circunstâncias é permissível uma mulher fazer um aborto, se a pena de morte é errada, se as pessoas devem ter o direito de usar armas, até que ponto é aceitável o uso de animais em experiências científicas e que tipo de conduta é apropriado durante uma guerra. Um segmento importante da ética aplicada, no qual se incluem algumas destas questões, é a bioética.
A metaética é a terceira área principal da filosofia moral, distinguindo-se das outras duas não só por ser mais abstracta (ver abstracto e concreto), mas também por não possuir um carácter normativo (ver normativo e descritivo). Nesta área, o objectivo não é saber o que devemos fazer ou valorizar, isto é, não é defender determinados juízos morais — na metaética discute-se antes o que querem dizer os nossos juízos morais e como podemos avaliá-los. Ver contratualismo, ética das virtudes. (Pedro Galvão)
Singer, Peter, Ética Prática (Lisboa: Gradiva, 2000).
ética aplicada
Ramo da ética também designado “ética prática” em que, diferentemente da metaética e das teorias normativas da ética, se discutem directamente questões práticas da ética como o aborto, a eutanásia, a pena de morte, a clonagem, a pobreza, o ambiente, a pornografia, etc. Ver também bioética. (Aires Almeida)
ética das virtudes
Inspirados em Aristóteles, os que defendem uma ética das virtudes procuram geralmente uma alternativa tanto à ética consequencialista como à ética deontológica. Ao passo que estes dois tipos de ética se concentram na procura de princípios morais que regulem a conduta, a ética das virtudes tenta examinar os traços de carácter próprios de um agente virtuoso, como a coragem, a benevolência ou a honestidade. Assim, para muitos defensores da ética das virtudes o que interessa primariamente não é saber que actos devemos realizar, mas que tipo de pessoa devemos ser. (Pedro Galvão)
ética deontológica
Quem defende uma ética deontológica, por oposição a quem defende uma ética consequencialista, pensa que agir moralmente não é apenas uma questão de produzir bons resultados e evitar maus resultados. Os deontologistas defendem que temos deveres que nos obrigam a não realizar certos tipos de actos, de tal maneira que não podemos realizá-los mesmo quando a sua realização permitiria evitar um mal maior. Afirmam, por exemplo, que temos o dever de não matar pessoas inocentes, querendo dizer com isso que é errado matar uma pessoa inocente mesmo que matá-la seja a única maneira de impedir que alguém mate várias pessoas inocentes. Ver dever, direitos, imperativo categórico. (Pedro Galvão)
eudaimonia
Termo grego para eudemonia: bem-estar ou felicidade. Segundo Aristóteles, a felicidade não consiste na posse de bens materiais e é o máximo bem a que todas as pessoas naturalmente aspiram. Para o estoicismo, a felicidade não é um fim (telos), como para Aristóteles, mas simplesmente algo que resulta da vida harmoniosa. (Aires Almeida)
eugenia
O termo foi criado em 1883 por Francis Galton, influenciado pela ideia de selecção natural, de Darwin, para designar a selecção de características hereditárias de modo a melhorar as gerações futuras. Entre os meios habitualmente propostos para atingir esse objectivo contam-se os cruzamentos selectivos, o controlo da natalidade, os cuidados pré-natais, a fertilização in vitro e a engenharia genética. Estes meios são geralmente designados por “eugenia positiva”. Outros meios incluem o aborto, o infanticídio, a eutanásia, a esterilização forçada e a eliminação de populações consideradas geneticamente defeituosas. Estes meios caem sob a designação de “eugenia negativa”, e foram largamente implantados na Alemanha nazi, entre meados da década de 30 do séc. XX e o termo da Segunda Guerra Mundial. Durante os anos 30, a eugenia foi defendida por intelectuais proeminentes, como George Bernard Shaw e John Maynard Keynes, e condenada por outros, como G. K. Chesterton, que a considerava imoral. Nessa época, todavia, a ideia conheceu considerável popularidade nos meios científicos, tendo-se tornado, inclusivamente, uma disciplina académica em muitas universidades. A ideia de eugenia contribuiu para o investimento no combate a doenças hereditárias como a hemofilia ou a doença de Huntington. A sua reputação científica, porém, decaiu significativamente não só na sequência das políticas raciais da Alemanha nazi, mas também devido ao debate acerca da sua eventual contaminação por conceitos extracientíficos como os de classe social ou pureza racial. Actualmente, os desenvolvimentos da genética e das tecnologias reprodutivas relançaram o debate sobre se, e até que ponto, certas práticas são ou não eugénicas e se serão, nesse caso, morais ou imorais. (Artur Polónio)
Êutifron, dilema de
Ver dilema de Êutifron.
exclusão, falácia da
Ver falácia da exclusão.
existência
A questão de saber que coisas existem é o tema central em ontologia. Discutem-se assuntos como a existência ou não de objectos abstractos, tais como universais, proposições (ver proposição) e números, e que tipo de existência têm objectos ficcionais como Sherlock Holmes ou Frodo Baggins. Uma segunda questão é a de saber o que é a existência. Alguns filósofos defendem que a existência é (pelo menos por vezes) uma propriedade de objectos isto é, uma propriedade de primeira ordem como a propriedade de ser alto ou bonito. Outros filósofos defendem que a existência nunca é uma propriedade de objectos, mas antes uma propriedade de propriedades isto é, uma propriedade de segunda ordem. Ou seja, quando dizemos que Pégaso não existe, não estamos a dizer que Pégaso não tem a propriedade da existência mas que a propriedade de ser Pégaso não tem objectos na sua extensão isto é, nada existe com a propriedade de ser Pégaso. (Célia Teixeira)
existência, sentido da
Ver sentido da vida.
existencial, quantificador
Ver quantificador existencial.
existencialismo
Movimento filosófico constituído por diversas doutrinas unidas por dois aspectos fundamentais: 1) o objecto da sua reflexão é a existência humana entendida como realidade individual concreta que não se explica nem se demonstra mas unicamente se descreve; 2) reage contra a identificação hegeliana entre realidade e racionalidade porque a existência não está iluminada pela luz da razão. Afirmar, como o fez Hegel que tudo o que é real é racional implica desvalorizar os aspectos dramáticos, angustiantes, imprevisíveis e absurdos que caracterizam a existência humana. O existencialismo pretende falar do ser humano concreto. Nada lhe dizem as ideias ou noções abstractas nem os grandes sistemas racionais que tudo julgam poder explicar e solucionar. O que lhe interessa é descrever o indivíduo, a realidade singular em devir, dramaticamente comprometida ou envolvida nas suas escolhas e opções. O principal representante da corrente existencialista é Sartre, embora se considere que as raízes da filosofia existencialista remontam pelo menos a Kierkegaard. O filósofo dinamarquês revoltou-se contra a crença tipicamente hegeliana de que a razão podia resolver os problemas fundamentais da vida fossem eles morais, religiosos, políticos ou artísticos. O resultado desta confiança cega na razão foi a construção de poderosos sistemas filosóficos que tudo pretendiam explicar mas cujo grau de abstracção era tal que perdiam de vista a realidade concreta individual ou lhe atribuíam pouca importância. Autenticidade, responsabilidade, escolha, angústia, singularidade, absurdo, são alguns dos conceitos que o movimento existencialista encontra em Kierkegaard e utilizará conforme a orientação dos seus representantes. Sartre representa o existencialismo ateu, Gabriel Marcel o existencialismo cristão. Outros pensadores, como Heidegger e Karl Jaspers (1883–1969), e Albert Camus (1913–1960), são por alguns historiadores da filosofia incluídos neste movimento muito heterogéneo. (Luís Rodrigues)
experiência
Conhecimento que se obtém directamente da observação do mundo à nossa volta. Diz-se que se obtém directamente porque não é o resultado de qualquer inferência. Em termos mais precisos, dá-se o nome de “experiência” aos dados dos sentidos, ou sensações, em que tal conhecimento se baseia. Finalmente, o termo usa-se ainda, no sentido de experimentação, para referir o que os cientistas fazem para testar e compreender as consequências das suas teorias, nomeadamente através da manipulação de fenómenos e de simulações laboratoriais. Ver também empirismo. (Aires Almeida)
experiência estética
Diz-se muitas vezes que uma experiência é estética se for originada por objectos belos ou obras de arte. Alguns filósofos consideram este um tipo especial de experiência, diferente de qualquer outra experiência, e que só ocorre quando contemplamos objectos estéticos. Kant procura caracterizar (se bem que indirectamente, referindo-se antes aos juízos) a diferença que há entre uma experiência estética e uma experiência não-estética, dizendo que aquela é desinteressada e esta não. Quer com isso dizer que a experiência estética não procura satisfazer qualquer tipo de necessidade prática nem tem qualquer finalidade exterior a si. Esta caracterização não é aceite por aqueles que consideram haver experiências marcadas pelo desinteresse, mas que não são estéticas, como jogar matraquilhos. Alguns filósofos defendem que a estética consiste na análise e discussão da experiência estética. Outros, como o filósofo americano George Dickie (n. 1926), acham que não existe tal coisa. Ver também atitude estética e juízo estético. (Aires Almeida)
experiência mental
Na impossibilidade de realizar experiências científicas (ver experiência), muitos filósofos desenvolvem situações ou acontecimentos imaginários, a que se dá o nome de “experiências mentais”. As experiências mentais são uma forma de saber até que ponto as teorias filosóficas são plausíveis e, simultaneamente, uma forma de argumentar, estabelecendo casos possíveis que as possam refutar. De filósofos antigos, como Platão e a sua alegoria da caverna, a contemporâneos, como John Searle e o seu Quarto Chinês, passando por Descartes e o seu génio maligno, são muitos os que recorrem a experiências mentais. (Aires Almeida)
experiência religiosa
1. Diz-se daquele tipo de experiência em que se tem uma percepção ou se sente a manifestação de uma divindade. Um exemplo de uma experiência desse tipo é a que é atribuída aos Pastorinhos de Fátima quando afirmam ter visto Nossa Senhora. A existência ou não de experiências religiosas tem um papel importante em filosofia da religião, pois estas são por vezes usadas como prova da existência de Deus. A experiência religiosa é discutida no âmbito da epistemologia da religião.
2. Num sentido popular, as actividades decorrentes da prática de uma religião, como ir à missa e rezar, são vistas como experiências religiosas. Ver milagres, filosofia da religião. (Célia Teixeira)
explicação científica
Numa explicação, o explanandum é aquilo que queremos explicar; o explanans consiste na informação aduzida para explicar aquilo que queremos explicar. Segundo a perspectiva padrão, todas ou muitas das explicações científicas obedecem ao modelo nomológico-dedutivo. De acordo com este modelo, explicar cientificamente um acontecimento é mostrar que, dadas as condições reunidas na altura da sua ocorrência (as chamadas “condições iniciais”) e as leis da natureza, esse acontecimento tinha de ocorrer. Por exemplo, imagine-se que queríamos explicar a dilatação de um certo pedaço de metal. A explicação poderia apresentar-se assim: 1) Todo o metal dilata quando é aquecido; 2) Este pedaço de metal foi aquecido; 3) Logo, este pedaço de metal dilatou. Em 3 encontramos o explanandum, isto é, o acontecimento que queremos explicar. Em 1 e 2 encontramos o explanans — uma lei da natureza e uma condição inicial, respectivamente. Explicamos o acontecimento deduzindo 3 da lei e da condição. Muitos filósofos pensam que este modelo não se aplica às ciências sociais. Ver argumento, dedução, lei da natureza, unidade da ciência. (Pedro Galvão)
explícita, definição
Ver definição explícita.
extensão
1. A extensão de um termo é a totalidade dos objectos a que se refere. Por exemplo, a extensão do predicado “ser português” é o conjunto dos portugueses. Dois termos com a mesma extensão podem exprimir conceitos diferentes e assim ter intensões (com s) diferentes: “O Presidente da República em 2003” e “O marido de Maria José Ritta” têm ambos como extensão Jorge Sampaio, mas identificam-no através de condições diferentes. Diz-se que, numa frase, uma expressão ocorre num contexto extensional quando pode ser substituída por uma expressão com a mesma extensão sem que isso altere o valor de verdade da frase; caso contrário, diz-se que ocorre num contexto intensional. Assim, em “João viu a Miss Portugal”, a expressão nominal “a Miss Portugal” ocorre num contexto extensional, pois se a substituirmos por “a filha do Mendes" (por hipótese, com a mesma extensão) o valor de verdade da frase original não se altera. Pelo contrário, em “João procura a Miss Portugal”, a mesma expressão ocorre num contexto intensional, visto que essa frase e “João procura a filha do Mendes” podem ter valores de verdade diferentes (o João pode procurar a Miss Portugal sem saber que ela é a filha do Mendes).
2. A propriedade daquilo que é extenso, isto é, do que tem existência material (ver matéria). Ver também intensão, referência. (Pedro Santos)
F
facto e valor
Ver juízo de facto e juízo de valor.
falácia
Um argumento mau que parece bom. Os argumentos podem ser falaciosos 1) por serem inválidos e parecerem válidos, por 2) terem premissas falsas que parecem verdadeiras, ou por 3) não serem cogentes mas o parecerem. Por exemplo, o argumento seguinte é inválido mas parece válido: “Todas as coisas têm uma causa; logo, há uma causa para todas as coisas”. O argumento seguinte tem uma premissa falsa, mas não parece: “Ou gostas de Picasso ou odeias Picasso; dado que não gostas, odeias.” O argumento seguinte pode parecer cogente, mas não é: “Se os cépticos tivessem razão, nada se poderia saber; mas como é óbvio que se pode saber várias coisas, os cépticos não têm razão”.
A distinção entre argumentos maus que são enganadores porque parecem bons e argumentos maus que não são enganadores porque não parecem bons não é formal mas sim informal. Esta distinção é crucial, uma vez que são as falácias que são particularmente perigosas. Os argumentos obviamente maus não são enganadores e, se todos os argumentos maus fossem assim, não seria necessário estudar lógica para saber evitar erros de argumentação.
Prova-se que um argumento é falacioso mostrando que é possível, ou muito provável, que as suas premissas sejam verdadeiras mas a sua conclusão falsa; ou que tem premissas subtilmente falsas; o que as premissas não são mais plausíveis do que a conclusão.
Quando se diz que uma definição, por exemplo, é falaciosa, quer-se dizer que é enganadora ou que pode ser usada num argumento que, por causa disso, será falacioso. Ver refutação. (Desidério Murcho)
falácia ad hominem
(ataque à pessoa) Falácia pela qual se pretende refutar (ver refutação) uma afirmação, atacando, ou desvalorizando de alguma maneira, a pessoa que a defendeu. Pode assumir a forma de ataques ao carácter, à raça, à religião ou à nacionalidade da pessoa. Exemplo: “O meu pai diz que não se deve fumar, mas fuma. Logo, não há razões para deixar de fumar”. Neste caso, pretende-se refutar a ideia de que não se deve fumar atacando a pessoa que a defendeu por ela ser incoerente. (Júlio Sameiro)
falácia da afirmação da consequente
Falácia que consiste em supor que da condicional “Se P, então Q” e da afirmação da consequente dessa condicional, “Q”, se pode concluir “P”. Exemplo: “Se jogamos bem, então ganhamos o jogo. Ganhámos o jogo. Logo, jogámos bem”. é fácil apresentar uma refutação desta forma de argumento com um contra-exemplo com a mesma forma lógica: o argumento “Se isso é sardinha então isso é peixe. É peixe. Logo, é sardinha”., implicando a falsidade “Basta ser peixe para ser sardinha”, mostra que este padrão argumentativo é falacioso. (Júlio Sameiro)
falácia da circularidade
1. Um argumento cuja conclusão esteja explícita ou implicitamente contida nas premissas; chama-se petição de princípio ou petitio principii a este tipo de falácia. Os casos mais evidentes são aqueles em que a conclusão se limita a repetir a premissa: “Deus existe porque diz na Bíblia e a Bíblia é a palavra de Deus”. Os casos mais subtis incluem variações gramaticais: “Os animais não têm direitos porque não são contemplados na legislação”. É falso que nos argumentos dedutivos válidos a conclusão esteja “contida” nas premissas, como por vezes se pensa. Pois há argumentos dedutivos válidos cujas conclusões não estão “contidas” nas premissas: “Sócrates é grego; logo, Sócrates é grego ou os livros estão errados”. E há argumentos dedutivos inválidos cujas conclusões estão “contidas” nas premissas: “Se Sócrates tivesse nascido em Estagira, seria grego; Sócrates era grego; logo, Sócrates nasceu em Estagira”.
2. Uma definição é falaciosamente circular se definir A em termos de B e depois B em termos de A, sem com isso esclarecer A. Por exemplo: “Uma pessoa solteira é uma pessoa não casada”. E o que é uma pessoa casada? “É uma pessoa não solteira”. Um certo grau de circularidade nas definições é aceitável, desde que se trate de uma circularidade informativa. Por exemplo, as definições científicas de massa, peso, energia, força, etc., acabam por ser circulares, mas são informativas. (Desidério Murcho)
falácia da composição
Falácia que consiste em concluir que, por as partes de um todo ou os elementos de uma classe terem uma propriedade, o todo ou a classe também devem ter tal propriedade. Exemplo: “As células não têm consciência. Portanto, o cérebro, que é feito de células, não tem consciência.” Provamos que esta forma de argumento é falaciosa com exemplos simples como, por exemplo, “O oxigénio e o hidrogénio não são bebíveis. Logo, a água não é bebível”. (Júlio Sameiro)
falácia da divisão
Falácia que consiste em atribuir às partes de um todo ou aos elementos de uma classe uma propriedade do todo ou da classe. “F é uma excelente equipa. i joga na equipa F. Logo, i é um excelente jogador." contra-exemplo: “A classe dos números é infinita. Ora 2 é um número. Logo, 2 é infinito”. (Júlio Sameiro)
falácia da exclusão
São frequentes os argumentos que omitem conhecimentos relevantes para avaliar uma conclusão. Por exemplo: uma pessoa empenhada em provar que as guerras são inevitáveis e que se limite a coleccionar os exemplos favoráveis oferecidos pela história, incorre nesta falácia por excluir conhecimentos relevantes — deveria, por exemplo, explicar por que razão a Suíça, estando trezentos anos sem guerrear, não é um contra-exemplo que arruína a sua tese. (Júlio Sameiro)
falácia da falsa analogia
Um argumento analógico é fraco quando sobrevaloriza as semelhanças entre duas ou mais coisas ou quando despreza diferenças relevantes. Os casos mais extremos são falsas analogias. O argumento “Uma casa teve um arquitecto e tem um senhor; assim o Universo, a casa de todos, teve um arquitecto e tem um senhor — Deus” é um caso óbvio de falsa analogia porque a pretensa semelhança entre “casa” e “Universo” é apenas um efeito literário e retórico. Ver também falácia, analogia e argumento por analogia. (Júlio Sameiro)
falácia da negação da antecedente
Falácia que consiste em supor que, se uma condicional, “Se P, então Q”, e a negação da sua antecedente, isto é, “não P”, forem verdadeiras, a negação da sua consequente, isto é, “não Q”, também é verdadeira. Exemplo: “Se copiaste, acertaste. Não copiaste. Logo, não acertaste”. Apesar de ser fácil apresentar contra-exemplos — “Se Camões é espanhol, então é ibérico. Camões não é espanhol. Logo, Camões não é ibérico" — é uma falácia muito frequente. (Júlio Sameiro)
falácia da pergunta complexa
Pergunta formulada de tal modo que uma resposta directa compromete a pessoa com mais do que uma afirmação. Cria-se esta falácia incluindo na pergunta afirmações ou suposições às quais o interrogado ainda não assentiu. A pergunta “Já deixaste de copiar?” só deve ser aceite por quem já reconheceu ter copiado porque tanto o “sim" como o “não” são comprometedores: o “sim” será interpretado como confissão de que a pessoa copiou; o “não” será interpretado como confissão de que a pessoa ainda copia. (Júlio Sameiro)
falácia do apelo à força
Argumento que, para defender a sua conclusão, apresenta ameaças em vez de razões. As ameaças podem ser directas ou consequências possíveis e apenas sugeridas. Exemplo: “Isso talvez seja verdadeiro mas se o afirmar a empresa terá de prescindir dos seus serviços”. O apelo à força é legítimo em algumas circunstâncias, por exemplo para fazer cumprir a lei ou como conselho técnico destinado a evitar acidentes. (Júlio Sameiro)
falácia do apelo à ignorância
Argumento em que, confessada a ignorância sobre a verdade de uma afirmação, se conclui que a afirmação é falsa (ou que da ignorância sobre se uma afirmação é falsa se conclui que ela é verdadeira). Exemplos clássicos de apelos à ignorância falaciosos (ver falácia): “Ninguém provou que Deus existe. Logo, Deus não existe”, “Não há provas de que Deus não exista. Logo, Deus existe”, “Ninguém sabe qual é a causa natural de X. Logo, X tem uma causa sobrenatural”. Há apelos à ignorância não falaciosos. Por exemplo: se uma pessoa acusa o nosso pacato vizinho de ser um ladrão mas não apresenta indícios, devemos rejeitar a acusação. Em geral, o apelo à ignorância é legítimo se a negação da sua conclusão colide com o conhecimento comum. (Júlio Sameiro)
falácia do apelo à piedade
Um apelo à piedade do auditório é falacioso (ver falácia) se puser em segundo plano os factos ou critérios que devem justificar uma afirmação. Exemplo: “O professor deve dar-me o 18 porque de outra maneira não entro em medicina e a minha vida atrasa-se”. é um apelo ao sentimento de piedade do professor para que este altere os seus critérios. (Júlio Sameiro)
falácia do apelo ao povo
Esta falácia caracteriza-se pelo apelo às emoções de um grupo ou à suposta sabedoria partilhada por todos (povo). Em regra, este apelo a emoções ou saberes comuns apela a motivos e não a razões. Exemplo: “Todas as pessoas sensatas rejeitam X. Logo, deves rejeitar X”. Neste caso, espera-se que o desejo de ser incluído na classe das pessoas sensatas leve o auditório a aprovar a conclusão. (Júlio Sameiro)
falácia do apelo às consequências
Falácia, ou classe de falácias, em que possíveis consequências práticas de uma proposição são usadas como prova. Exemplo: “Se toda a ordem fosse apenas aparente, o mundo seria inquietante. Logo, a ordem não é apenas aparente.” Neste caso espera-se que o desejo de segurança do auditório o leve a rejeitar uma proposição e a tomar a sua negação como verdadeira. (Júlio Sameiro)
falácia do falso dilema
Falácia que consiste na suposição de que, sobre um determinado assunto, só há duas alternativas quando de facto há mais. Exemplos: “Estás com a América ou contra a América”., “És rico ou pobre”., “És bom ou mau”. Estas suposições falsas são muitas vezes usadas como premissas de argumentos dedutivos válidos (ver validade), do género: “Estás com a América ou contra a América: Não estás com a América; logo, estás contra a América”. Ver também disjunção. (Júlio Sameiro)
falácia do homem de palha
Esta falácia consiste em atacar as ideias de uma pessoa apresentando-as numa versão deficiente ou distorcida. Constitui uma violação do princípio de caridade — a exigência de que, no debate racional, se ataque a versão mais sólida das ideias que queremos contestar. Exemplos desta falácia: “A única razão para defender a pena de morte é o desejo primitivo de vingança”., “Reprovaram-me porque só olharam para o meu comportamento”. (Júlio Sameiro)
falácia genética
Esta falácia ocorre quando, para avaliar uma teoria ou afirmação, se invocam factores do contexto de descoberta que são irrelevantes como prova. Em regra, é falacioso apelar a contextos históricos ou sociais ou às circunstâncias psicológicas em que surgiu uma teoria para legitimar um juízo sobre essa teoria. Exemplos: os nazis cometeram a falácia genética ao desvalorizar as teorias de Einstein por este ser judeu; muitas pessoas acreditam falaciosamente que o casamento monogâmico é a única forma de família legítima apenas com base na sua longa história. Ver também relativismo. (Júlio Sameiro)
falácia post hoc
Falácia também designada “depois disso, por causa disso” porque consiste em presumir que se dois acontecimentos são sucessivos, então o primeiro é causa do segundo. “Ingeriu o mel e a constipação passou. Logo, o mel é bom para tratar constipações”., “Rezou e a sorte mudou. Logo, rezar é eficaz para mudar o curso dos acontecimentos”. Na base desta falácia pode estar a sobrevalorização de sequências acidentais, o descarte de possíveis causas subjacentes ou o simples desejo de acreditar. (Júlio Sameiro)
falsa analogia, falácia da
Ver falácia da falsa analogia.
falsidade lógica
Ver contradição.
falsificabilidade
Diz-se do que é falsificável. Uma teoria (ou proposição) é falsificável quando pode ser submetida a testes empíricos que a possam refutar. E uma teoria está falsificada quando é realmente refutada por dados empíricos quando se mostra que é falsa. Não se pode confundir a noção de falsificado com a de falsificável. Se uma teoria foi falsificada, então é falsa. Todas as boas teorias científicas são falsificáveis, mas não são, claro está, todas falsas. Por exemplo, a proposição de que a Lua gira em torno da Terra é falsificável, pois seria possível observar que a Lua afinal não girava em torno da Terra, se ela não girasse. Mas a proposição de que a posição dos astros influencia o comportamento das pessoas não é falsificável, pois não é possível observar seja o que for que a falsifique. Karl Popper usou esta noção, central na sua filosofia da ciência, para responder ao problema da demarcação (ver critério de demarcação). Ver falsificacionismo. (Célia Teixeira)
falsificacionismo
Teoria de filosofia da ciência proposta por Karl Popper como forma de responder ao problema da indução. Em A Lógica da Pesquisa Científica (1934, trad. Cultrix, 1974) e Conjecturas e Refutações (1963; trad. Almedina, 2003) Popper defende que os cientistas não chegam às suas teorias pelo método de generalizações a partir de observações. A ideia é que os cientistas começam por propor as suas teorias (ou conjecturas) sujeitando-as depois a rigorosos testes. Ou seja, o que está na base do método científico não é a indução, mas um processo de conjecturas e refutações. Quando uma teoria passa o teste empírico, diz-se que foi corroborada (ver corroboração) continuando a ser desenvolvida e testada. Quando falha o teste, é falsificada e consequentemente abandonada. Uma teoria é tanto melhor quanto maior for o seu grau de falsificabilidade, dado que quantas mais previsões fizer maiores serão os riscos de refutação. Ver critério de demarcação. (Célia Teixeira)
falsificado
Ver falsificabilidade.
falsificável
Ver falsificabilidade.
falso dilema, falácia do
Ver falácia do falso dilema.
fé
Crença na existência de um Deus ou deuses. Em contextos não religiosos, a palavra refere-se unicamente a uma crença muito forte; por exemplo, quando dizemos que temos fé na recuperação de uma doença. Ver, filosofia da religião, fideísmo. (Célia Teixeira)
fenómeno
Palavra de origem grega que, em geral, designa o que aparece à consciência e tem origem nos sentidos, por oposição ao que é apreendido apenas pelo intelecto. Em Platão, o fenómeno é o que pertence ao mundo sensível, enquanto o númeno (a ideia ou Forma) pertence ao mundo inteligível. Para Kant, o fenómeno é o objecto da experiência possível, o que é dado no espaço e no tempo e opõe-se ao númeno ou coisa em si. (Álvaro Nunes)
fenomenologia
Termo pelo qual é designado o movimento filosófico surgido a partir da obra de Edmund Husserl (1859–1938) e que tem por objectivo principal a investigação e a descrição dos fenómenos (ver fenómeno) tal como ocorrem na consciência, independentemente de quaisquer preconceitos, pressupostos ou teorias explicativas. É possível detectar pelo menos quatro tendências principais neste movimento: a fenomenologia realista, que põe ênfase na descrição das essências (ver essência) universais (Nicolai Hartman, Max Scheler); a fenomenologia constitutiva, que procura dar conta dos objectos em termos da consciência que temos deles (Dorion Cairns, Aron Gurwitsch); a fenomenologia existencial (ver existência), que realça a existência humana no mundo (Hannah Arendt, Jean-Paul Sartre e Maurice Merleau-Ponty); e a fenomenologia hermenêutica (ver hermenêutica), que realça o papel da interpretação em todas as esferas da vida (Hans-Georg Gadamer, Paul Ricoeur). (Álvaro Nunes)
Feyerabend, Paul (1924–1994)
Filósofo da ciência americano, de origem austríaca, que advogava a inutilidade da própria filosofia da ciência. Segundo Feyerabend, qualquer tentativa de identificar um método, ou sequer um conjunto de métodos, na história da ciência está condenada ao fracasso. Isto acontece porque, segundo ele, a ciência tem tanto de racional — e de irracional — como qualquer outra actividade humana, seja ela a religião, a alquimia ou o ocultismo. O chamado “sucesso” da ciência deve tanto à razão como ao desleixo, ao caos, ao acaso, à incompetência, à retórica ou ao oportunismo dos cientistas. Longe de se procurar eliminar estes aspectos, é até desejável que eles actuem livremente no seio da ciência. Por isso Feyerabend se opõe à ideia de método e defende uma concepção anarquista da ciência. Considera também irrelevante a questão de saber o que distingue a actividade científica de outras actividades não-científicas. As ideias de Feyerabend, principalmente defendidas em obras como Contra o Método (1975; trad. 1993, Relógio d'Água) e Adeus à Razão (1987; trad. 1991, Edições 70), foram fortemente criticadas por vários filósofos da ciência, entre os quais Karl Popper. Ver também método científico. (Aires Almeida)
fideísmo
A tese segundo a qual as crenças religiosas não são susceptíveis de discussão racional. A ideia é que as questões religiosas não podem ser justificadas por meio de argumentos ou provas, mas apenas pela fé. Os fideístas mais radicais, como Kierkegaard, defendem que justificar a nossa crença em Deus é não só impossível, pois Deus está para lá da nossa compreensão, como uma má opção, pois ao fazê-lo estamos a retirar o que há de essencial à própria fé. Este tipo de fideísmo é assim uma forma de irracionalismo cujo mote é: “acredito porque é absurdo”. Já Blaise Pascal (1623–1662) e Santo Agostinho defendem uma forma mais moderada de fideísmo segundo a qual, apesar de a fé ter um estatuto privilegiado em matérias religiosas, podemos apelar à razão para a fundamentar. Ver Aposta de Pascal. (Célia Teixeira)
filosofia
O estudo dos problemas de carácter mais geral e conceptual que afectam o nosso pensamento científico, religioso, artístico e quotidiano, para os quais não há respostas científicas. Eis alguns exemplos de problemas filosóficos: Será tudo relativo e mera opinião? Será que temos livre-arbítrio? O que é o conhecimento? Será o conhecimento possível? Como devemos viver? O que é o bem moral e qual é o seu fundamento? O que é a justiça? Dizer que os problemas da filosofia são conceptuais é dizer que não são problemas que se possam decidir recorrendo à experiência. Neste aspecto, a filosofia é como a matemática, e não como a história ou a física.
O método da filosofia é a discussão racional de argumentos. Isto significa que não há métodos formais nem científicos de prova, como na matemática ou na física; tudo o que se pode fazer é pensar tão correctamente quanto possível, procurando soluções adequadas.
Os primeiros filósofos não faziam uma distinção profunda entre as diferentes áreas do conhecimento. Aristóteles, por exemplo, dedicou-se não apenas ao que hoje reconhecemos como filosofia, mas também à física, astronomia, biologia, etc. Para os primeiros filósofos, o estudo da filosofia tinha muito mais em comum com a biologia, a matemática ou a história, do que com outras manifestações culturais como a arte ou a religião. E o que tinha em comum era o estudo racional da natureza das coisas e a procura da verdade. A filosofia surge assim associada, juntamente com as outras áreas do conhecimento, à própria ideia de investigação livre, opondo-se à atitude dogmática que consiste em proclamar pretensas “verdades” que não se podem colocar em causa.
A filosofia não é coisa do passado. Apesar da sua longa história (ver filosofia, história da), a filosofia continua viva; na verdade, há talvez mais filósofos hoje em dia do que ao longo de toda a história da humanidade. E também não é verdade que não exista progresso em filosofia; sem dúvida que a compreensão actual dos problemas, teorias e argumentos da filosofia é superior à de qualquer época do passado. Simplesmente, talvez não haja na filosofia o tipo de progresso por acumulação de resultados que podemos encontrar na ciência. O progresso da filosofia é um alargamento da compreensão. Podemos continuar sem conseguir provar se temos ou não livre-arbítrio, ou se Deus existe ou não, ou sequer como se pode justificar a nossa crença no mundo exterior; mas a compreensão que temos hoje destes problemas é mais profunda do que a que se tinha no passado.
Não se pode exigir do filósofo, ou do estudante de filosofia, respostas definitivas como temos em medicina, por exemplo, em que é possível dizer exactamente o que provoca a diabetes, ou como se cura a tuberculose. Mas isto não significa que as opiniões dos filósofos, ou do estudante de filosofia, sejam “meras opiniões”, incomensuráveis, subjectivas e pessoais, insusceptíveis de avaliação racional e de estar mais ou menos próximas da verdade ou da plausibilidade. A opinião que se espera de um filósofo, ou de um estudante de filosofia, é como a opinião que se espera de um médico quando vamos a uma consulta: uma opinião fundamentada e informada, que se pode discutir e avaliar racionalmente. O objectivo do estudo da filosofia é saber avançar “diagnósticos”, tão bons quanto possível, relativamente aos problemas tradicionais da filosofia. Isto exige um bom conhecimento do que está em causa e das diferentes respostas que tentam resolver esse problema, tanto antigas como modernas. Exige a capacidade para compreender os diferentes aspectos dos problemas, os diferentes mecanismos de argumentação ou fundamentação e as diferentes maneiras como uma teoria ou ideia pode ser melhorada para responder a objecções e contra-exemplos.
As principais disciplinas da filosofia merecem artigos próprios neste dicionário: metafísica, epistemologia, ética, lógica, filosofia da religião, filosofia política, estética, filosofia da ciência, filosofia da mente, filosofia da linguagem, filosofia da acção. (Desidério Murcho)
Nagel, Thomas, Que Quer Dizer Tudo Isto? (Lisboa: Gradiva, 1995).
Russell, Bertrand, Os Problemas da Filosofia (Coimbra: Almedina, 2001).
Warburton, Nigel, Elementos Básicos de Filosofia (Lisboa: Gradiva, 1988).
filosofia analítica
Corrente surgida nos finais do séc. XIX na Inglaterra, Áustria e Alemanha. A filosofia analítica nunca foi um movimento unitário, sendo antes uma designação genérica para várias correntes particulares: 1) A abordagem de Russell e Frege, que procurava usar novos instrumentos lógicos para analisar a linguagem que usamos para exprimir os aspectos mais centrais da realidade; 2) O positivismo lógico austríaco, com origem em Moritz Schlick (1882–1936) e Carnap, e importado para o Reino Unido por A. J. Ayer (1910–1989); 3) A filosofia da linguagem corrente de Cambridge e Oxford, com origem em J. L. Austin (1911–1960). As duas últimas correntes foram entretanto abandonadas, e a primeira perdeu a sua centralidade. Hoje em dia, a filosofia analítica caracteriza-se por retomar os ideais gregos de discussão pública, racional e crítica de ideias, opondo-se sobretudo à prática académica da chamada “filosofia continental”, que tende a identificar a filosofia com a sua história e o trabalho filosófico com a interpretação de textos. (Desidério Murcho)
filosofia da acção
A filosofia da acção é uma disciplina com ligações à filosofia da mente e à metafísica e, ainda, à Psicologia e à Teoria da Decisão. Trata-se de uma área interdisciplinar e especializada da filosofia que tem como objecto central a acção e a razão prática.
Alguns dos problemas que trata são tipicamente metafísicos: O que é uma acção? O que distingue uma acção de qualquer outro acontecimento no mundo? Como distinguir as acções umas das outras? Como distinguir acções básicas de acções não básicas? Será o livre-arbítrio compatível com o determinismo?
Acerca do que é uma acção, os filósofos dividem-se entre concebê-la como um acontecimento particular concreto (ver abstracto e concreto), localizado no espaço e no tempo e discernível de qualquer outro; ou concebê-la como uma entidade abstracta que não tem localização espaciotemporal, mas que pode ser exemplificada através dos actos concretos realizados por um agente. Para estes últimos filósofos, a acção de estudar, por exemplo, é algo que não está localizado no espaço ou no tempo. Já para os primeiros filósofos, não existe a acção de estudar em abstracto — o que existe são pessoas concretas que estudam, num dado momento e num certo local. A resposta aos problemas da distinção das acções e da diferenciação entre acções básicas e acções não básicas depende da concepção de acção que cada filósofo partilha.
Outros problemas de filosofia da acção apelam a questões centrais da filosofia da mente, como a de saber qual o papel dos estados mentais intencionais na acção (ver intenção) e o de saber como se enquadra a acção nas relações de causalidade entre a mente e o corpo (ver dualismo e monismo).
Os filósofos da acção utilizam, ainda, os dados empíricos (ver empírico) acerca do comportamento proporcionados pela Psicologia para discutir o problema de saber se a crença na racionalidade humana é compatível com a irracionalidade exibida em numerosos comportamentos humanos (como a fraqueza da vontade ou as preferências irracionais); e recorrem aos instrumentos proporcionados pela moderna Teoria da Decisão (uma área da matemática aplicada) para a análise rigorosa da racionalidade das decisões.
Uma questão ainda mais abstracta diz respeito à natureza das explicações filosóficas da acção: serão elas teorias que apenas descrevem o modo como os seres humanos habitualmente agem? Ou, serão elas teorias que propõem modelos ideais segundo os quais todos os seres humanos racionais deveriam agir? Alguns filósofos inclinam-se para o carácter descritivo das teorias da acção, mas outros defendem o seu carácter normativo (ver normativo e descritivo). Uma vez mais, está em causa a justificação da crença na racionalidade humana. (António Paulo Costa)
Dennett, Daniel C., “A intencionalidade — a abordagem dos sistemas intencionais" in Tipos de Mentes (Lisboa: Temas e Debates, 2001).
Ricoeur, Paul, O Discurso da Acção (Lisboa: Edições 70, 1988).
Searle, John R., “Intenção e Acção" in Intencionalidade (Relógio d'Água, 1999).
filosofia da arte
Ramo da estética que se ocupa dos problemas filosóficos colocados pela arte, nomeadamente os problemas da definição de arte, do valor da arte e da avaliação das obras de arte. Os problemas acerca do gosto e do belo, não são, em rigor, problemas da filosofia da arte, mas da estética em geral, pelo que nem sequer são discutidos por muitos filósofos da arte. Apesar de gostarmos de muitas obras de arte por as considerarmos belas, não temos de gostar de um objecto para ser classificado como arte, assim como também não é necessário que seja belo. A ideia de que arte e beleza se identificam está bastante enraizada, porque durante muito tempo os próprios artistas perseguiram algum ideal de beleza. A filosofia da arte é actualmente uma disciplina filosófica com grande vitalidade, incluindo áreas mais especializadas da filosofia da arte, como a filosofia da música e a filosofia da literatura. Ver também problema do gosto e teoria do belo. (Aires Almeida)
filosofia da ciência
Disciplina que estuda os problemas filosóficos levantados pelas ciências da natureza e pelas ciências sociais. Embora muitos desses problemas tenham recebido uma atenção considerável pelo menos desde Aristóteles, foi sobretudo a partir do séc. XX que, graças a filósofos como Carnap, Popper e Quine, a filosofia da ciência se afirmou como disciplina.
Uma preocupação central na filosofia da ciência é compreender o método científico. Proporcionar tal compreensão implica enfrentar problemas como os seguintes: Que tipos de raciocínio figuram nas teorias científicas? O que torna uma teoria melhor do que outra? As teorias científicas podem dar-nos um conhecimento objectivo (ver objectivo e subjectivo) da realidade? Qual é a natureza e o papel da observação científica? Em que consiste uma explicação científica de um acontecimento? Será que todas as ciências usam o mesmo método fundamental?
Para além destes problemas, que se situam sobretudo no domínio da epistemologia, os filósofos da ciência ocupam-se de problemas de natureza metafísica. Por exemplo, os cientistas descobrem leis da natureza e dizem-nos como certos acontecimentos causam outros — os filósofos querem saber o que é uma lei da natureza e em que consiste a causalidade.
O desenvolvimento da filosofia da ciência tem levado ao aparecimento de áreas mais especializadas, como a filosofia da biologia ou a filosofia das ciências sociais. Nestas áreas, para além de se procurar uma compreensão minuciosa dos métodos das ciências em causa, examina-se o conteúdo de certas teorias científicas para esclarecer questões filosóficas. Na filosofia da física, por exemplo, tenta-se saber até que ponto a mecânica quântica apoia o indeterminismo.
Os filósofos do positivismo lógico investigaram o conhecimento científico de um modo muito abstracto (ver abstracto e concreto), sem atender ao seu desenvolvimento e à maneira como os cientistas trabalham. Mas nas últimas décadas, em grande medida devido à influência de Kuhn, a filosofia da ciência tem prestado uma atenção considerável ao estudo da história e da sociologia da ciência. Ver confirmação, corroboração, falsificacionismo, fisicismo, paradigma, reducionismo, unidade da ciência. (Pedro Galvão)
Harré, Rom, As Filosofias da Ciência (Lisboa: Edições 70, 1988).
Losee, John, Uma Introdução Histórica à Filosofia da Ciência (Lisboa: Terramar, 1997).
Warburton, Nigel, “Ciência" in Elementos Básicos de Filosofia (Lisboa: Gradiva, 1998).
filosofia da linguagem
A filosofia da linguagem estuda o funcionamento da linguagem corrente (designadamente no que diz respeito ao significado), socorrendo-se muitas vezes de linguagens formais como as da lógica clássica. A linguagem é objecto de interesse filosófico explícito pelo menos desde Platão, mas só no séc. XX a filosofia da linguagem se tornou tecnicamente rigorosa (particularmente na filosofia analítica). Associadamente, tornou-se popular a tese de que a filosofia da linguagem é a mais fundamental das disciplinas filosóficas, no sentido em que a discussão das teorias e dos argumentos pertencentes às outras pode ser identificada com a discussão do uso correcto dos termos usados nessas teorias e argumentos. Esta tese perdeu entretanto aceitação, mas é ainda uma preocupação típica dos filósofos analíticos a clareza e o rigor com que expõem os seus pontos de vista. Uma vez que se ocupa do significado linguístico, a filosofia da linguagem tem uma relação estreita com a metafísica (pois é chamada a pronunciar-se sobre os tipos de entidades extralinguísticas com os quais nos comprometemos quando usamos a linguagem) e com a filosofia da mente (pois analisa quer a nossa capacidade de produzir sequências linguísticas quer os conteúdos mentais que são comunicáveis linguisticamente). Como aconteceu em outras áreas da filosofia, muitos dos problemas e teorias historicamente associados à filosofia da linguagem autonomizaram-se e são hoje do domínio de outras disciplinas (por exemplo, a semântica e a pragmática). Tópicos estudados tipicamente em filosofia da linguagem são, além do significado, a referência, a verdade, a metáfora e a relação do significado com o uso da linguagem pelos falantes. (Pedro Santos)
filosofia da mente
Na tradição filosófica, termos como “alma”, “espírito” ou “intelecto” foram usados para referir, embora em contextos filosóficos diferentes e com significados nem sempre coincidentes, aquilo que os filósofos contemporâneos referem com o termo “mente”. A filosofia da mente é a disciplina que discute os problemas relacionados com a mente e os fenómenos mentais — a sua existência, a sua natureza, a sua relação com o mundo. Estes problemas possuem estreitas ligações com problemas da metafísica, da filosofia da linguagem, da epistemologia e da filosofia da ciência, mas não devem ser confundidos com os problemas empíricos da Psicologia (ver problema filosófico).
Sendo uma das disciplinas filosóficas que mais interesse suscitou ao longo da história, particularmente no séc. XX, os seus problemas centrais são a relação entre a mente e o corpo, o solipsismo, a causalidade mental e a intencionalidade (ver intenção). Por exemplo, os filósofos da mente procuram respostas para perguntas como: O que é a mente? Qual o seu lugar na natureza? Existe uma relação causal entre a mente e a matéria? Que razões temos para acreditar que existem outras mentes para além da nossa? O que é a intenção e qual é o seu papel na acção? Qual é a natureza dos acontecimentos mentais? O que está em causa quando falamos de pensamento, memória, emoção, sentimento ou imaginação? Será correcto dividir as funções mentais, ou existirá nelas uma certa unidade? Poderão as máquinas ser conscientes?
A variedade destes problemas suscitou o aparecimento de teorias que, não sendo as únicas, são porventura as mais influentes em filosofia da mente: as teorias dualistas sobre a relação entre a mente e o corpo, a que se opõem doutrinas monistas (ver dualismo e monismo) como o fisicismo; o externismo, que se caracteriza pela defesa de que quaisquer conteúdos mentais dependem causalmente de estados do mundo que são exteriores à mente, e a que se opõe o internismo; e o funcionalismo, segundo o qual os estados mentais devem ser descritos, não em virtude de quaisquer propriedades intrínsecas (ver propriedade), mas em virtude da relação causal que mantêm com outros estados mentais e da função que têm relativamente ao comportamento. Ver crença, desejo, idealismo e filosofia. (António Paulo Costa)
Nagel, Thomas, Que Quer Dizer Tudo Isto?, Cap. 3 (Lisboa: Gradiva, 1995).
Sagal, Paul, Mente, Homem e Máquina (Lisboa: Gradiva, 1996).
Warburton, Nigel, Elementos Básicos de Filosofia, Capítulo 6 (Lisboa: Gradiva, 1998).
filosofia da religião
O estudo filosófico dos conceitos e afirmações religiosas. Apesar da multiplicidade de religiões com diferentes cultos, mitos e práticas, os filósofos têm-se tradicionalmente centrado nas religiões dominantes no ocidente o judaísmo, o cristianismo e o islamismo. Uma das razões deve-se ao facto de estas religiões fornecerem visões complexas acerca do modo como o mundo e o universo se comportam, ao contrário do que se passa com as religiões orientais como o hinduísmo, o budismo e o confucionismo que se preocupam mais em propor formas de conduta e de viver. O que interessa em geral aos filósofos é saber se a visão religiosa do universo é ou não verdadeira. Comum às religiões ocidentais é a crença na existência de Deus. Deus é caracterizado como uma pessoa incorpórea e eterna, que criou o universo, que é sumamente boa (moralmente perfeita), que é toda-poderosa (omnipotente), que sabe tudo (omnisciente), que está em todo o lado (omnipresente), etc. Diz-se que este deus é o Deus teísta, e chama-se teísmo à crença na sua existência, de modo que não é de estranhar que os problemas que mais têm atraído a atenção dos filósofos sejam o da coerência do conceito de Deus e o da existência de Deus.
Um dos paradoxos clássicos relativamente à coerência do conceito de Deus é o de saber se Deus pode criar uma pedra tão pesada que Ele não a possa levantar. Se Deus é omnipotente, então pode criar tal pedra, mas se a criar então não é omnipotente, porque depois não pode levantá-la. Por outro lado, se não a pode criar, então não é omnipotente. Uma resposta a este problema é a de que Deus não pode criar impossibilidades lógicas. Outro problema é o de saber se a existência de Deus é compatível com a liberdade humana: se Deus sabe tudo, então sabe o que vamos fazer; mas, se sabe o que vamos fazer, então o que vamos fazer já está determinado; logo, não pode haver livre-arbítrio.
A questão de saber se Deus existe é a que mais tem interessado aos filósofos. São vários os argumentos a favor da existência de Deus, muitos deles apresentados na Idade Média. Por exemplo, só da autoria de Tomás de Aquino há cinco argumentos a favor da existência de Deus. Os principais tipos de argumentos a favor da existência de Deus são: o argumento ontológico, o argumento cosmológico e o argumento do desígnio. Estes argumentos ganharam um novo fôlego nas mãos de teístas contemporâneos como Alvin Plantinga (n. 1932) e Richard Swinburne (n. 1934), que defendem versões mais sofisticadas de alguns deles. Chama-se “teologia natural” ao estudo racional de Deus. A “teologia revelada” é o estudo de Deus baseado na fé e na revelação.
Dois outros problemas igualmente muito discutidos são o papel dos milagres enquanto provas da existência de Deus, a que David Hume levantou fortes objecções (ver milagre), e o problema do mal.
Muitos filósofos fideístas (ver fideísmo) defendem que a questão de saber se Deus existe não é susceptível de discussão racional: é uma questão fé.
Outros problemas igualmente importantes são os seguintes: Será que a existência de Deus é compatível com a liberdade humana? Será que existe vida depois da morte? Como compreender conceitos como o de fé, salvação e criação, entre outros? (Célia Teixeira)
Swinburne, Richard, Será que Deus Existe? (Lisboa: Gradiva, 1998).
Blackburn, Simon, Pense: Uma introdução à Filosofia, Capítulo 5 (Lisboa: Gradiva, 2001).
Ward, Keith, Deus, Fé e o Novo Milénio (Mem Martins: Publicações Europa-América, 2000).
Warburton, Nigel, Elementos Básicos de Filosofia, Capítulo 1 (Lisboa: Gradiva, 1998).
filosofia política
Disciplina filosófica centrada na natureza e função do estado que está muito ligada à ética e que, tal como esta, tem um carácter normativo (ver normativo e descritivo).
O problema fundamental desta disciplina é o de saber como deve o estado relacionar-se com os cidadãos. Este problema dá origem a questões mais específicas: o que legitima a autoridade do estado? Até que ponto e para que fins pode o estado limitar a liberdade dos cidadãos? Em que medida e em que aspectos deve o estado fomentar a igualdade entre os cidadãos? O que é (ou seria) um estado que exibisse uma perfeita justiça social? Se a democracia é a melhor forma de governo, o que explica a sua superioridade? Será que mesmo num estado democrático o recurso à desobediência civil por vezes se justifica? E o recurso à discriminação positiva? Será uma forma aceitável de reagir a desigualdades profundas?
Ao procurar respostas satisfatórias para estas perguntas, os filósofos propõem teorias que têm frequentemente resultados práticos importantes, mas por vezes inesperados. A filosofia política de Marx, por exemplo, desencadeou revoluções em inúmeros países. E o pensamento de Mill promoveu a liberdade de expressão e a igualdade política entre homens e mulheres. Apesar de ser uma das disciplinas filosóficas mais cultivadas desde a Antiguidade, durante o século passado a filosofia política acusou um certo declínio até que, nos anos 70, Rawls revitalizou a reflexão neste domínio com Uma Teoria da Justiça (1971, trad. 2001 Presença). Ver contratualismo, Maquiavel, utopia. (Pedro Galvão)
Warburton, Nigel, “Política" in Elementos Básicos de Filosofia (Lisboa: Gradiva, 1998).
filosofia, história da
Costuma-se dividir a história da filosofia ocidental em quatro períodos, de acordo com a divisão habitual da própria história. Fala-se assim de filosofia antiga (do séc. VI a.C. ao séc. III d.C.), medieval (sécs. III-XV), moderna (sécs. XVI-XVIII) e contemporânea (do séc. XIX aos dias de hoje).
A filosofia ocidental surgiu na Grécia antiga, no séc. VI a.C. Os primeiros filósofos gregos foram Pitágoras (c. 580–500 a.C.) e Tales de Mileto (c. 624-546 a.C.), sendo ambos igualmente os fundadores do que hoje chamamos “ciência" (que eles não distinguiam da filosofia). Os primeiros filósofos dedicaram uma especial atenção à cosmologia (que hoje é uma disciplina científica), isto é, ao estudo da origem e natureza última do universo. Sócrates e Platão dedicaram-se depois a problemas éticos e políticos, assim como a alguns aspectos mais conceptuais da filosofia. Fizeram da procura de definições explícitas de conceitos básicos como beleza, justiça e conhecimento a sua actividade principal. Aristóteles desenvolveu praticamente todas as áreas da filosofia e da ciência, e estabeleceu firmemente o estudo sistemático de problemas filosóficos e científicos. Fundaram-se várias escolas dedicadas ao estudo da filosofia e surgiram vários filósofos importantes.
No período medieval a filosofia foi estudada num contexto sobretudo religioso. Muitos filósofos deste período foram extraordinariamente perspicazes, tendo desenvolvido algumas ideias e argumentos hoje considerados centrais em filosofia, não só na filosofia da religião e na metafísica, mas também na ética, filosofia da linguagem e lógica. Alguns dos debates mais importantes da época incluem o problema dos universais, as provas da existência de Deus e a compatibilidade entre a presciência divina e o livre-arbítrio humano (a presciência é a capacidade para saber de antemão o que vai acontecer). Alguns dos mais destacados filósofos ocidentais do período medieval foram Santo Agostinho, Santo Anselmo (1033–1109) (ver argumento ontológico), Abelardo (1079–1142), Tomás de Aquino, Duns Escoto (c. 1265–1308) e Guilherme de Ockham.
No período moderno, a epistemologia foi considerada por muitos filósofos o ponto de partida da filosofia. Descartes tornou-se um dos mais influentes filósofos de sempre. Neste período, a oposição entre empirismo e racionalismo tornou-se central. Do lado racionalista, juntamente com Descartes, estão filósofos como Espinosa (1632–77) e Leibniz. Do lado empirista, filósofos como Hobbes, Locke, Berkeley e Hume. Hobbes, Locke, Hume e Espinosa deram uma atenção especial à ética e à filosofia política, que tinham sido negligenciadas por Descartes. Outros filósofos importantes deste período foram Voltaire (1694–1778) e Jean- Jacques Rousseau (1712–78). Kant prossegue o trabalho dos filósofos racionalistas e empiristas, ocupando-se sobretudo de ética, epistemologia e metafísica. A sua obra foi uma das mais influentes de sempre. Os seus sucessores alemães, Fichte (1762–1814) e Hegel, adoptaram o idealismo. Schopenhauer (1788–1860) adopta a filosofia de Kant, mas desenvolve uma filosofia pessimista, muito influente nos sécs. XIX e XX, segundo a qual a existência humana é completamente desprovida de sentido. Jeremy Bentham (1748–1832) desenvolve o utilitarismo, uma das mais importantes teorias éticas e políticas, e a principal rival da ética de Kant e da filosofia política de Marx.
No séc. XIX, e sobretudo a partir do séc. XX, a filosofia conhece uma vitalidade e diversidade que ultrapassa de longe qualquer período histórico anterior. Alguns filósofos alemães e franceses fundam correntes como o existencialismo, a fenomenologia e a hermenêutica; nestas áreas, destacam-se filósofos como Husserl, Heidegger e Sartre. Alguns filósofos ingleses e americanos deixam-se influenciar decisivamente pelo trabalho de Frege, Russell e Wittgenstein, recuperando o projecto original da filosofia: o estudo racional de problemas conceptuais. Sobretudo depois da segunda guerra mundial, florescem disciplinas antes negligenciadas, como a metafísica, a filosofia da religião, a filosofia da arte, a ética, incluindo a ética aplicada) e a filosofia política. A filosofia da ciência e a epistemologia atingem resultados de grande importância, assim como a filosofia da linguagem e a lógica, que em grande parte se autonomiza relativamente à filosofia. A filosofia, tal como as artes e as ciências, entra no séc. XXI com um grau de sofisticação, pertinência e alcance nunca antes atingido. (Desidério Murcho)
Kenny, Anthony, História Concisa da Filosofia Ocidental (Lisboa: Temas e Debates, 1999).
finalidade
Meta, objectivo ou fim de algo. A finalidade de uma acção é o resultado que se pretende obter com essa acção. Distingue-se as finalidades últimas das instrumentais. Apanhar o comboio pode ser uma finalidade instrumental, se temos por objectivo ir ao Algarve; mas beber um copo de leite pode ser uma finalidade última, se o fazemos unicamente por prazer. As finalidades instrumentais visam outras finalidades, ao passo que as finalidades últimas se esgotam em si. Em ética procura-se determinar quais são as finalidades racionais últimas, se é que existem. Em filosofia da acção discute-se se existe uma relação causal entre a acção e a sua finalidade, e qual dos termos desta relação é a causa e qual é o efeito: embora pareça adequado conceber a acção como causa e a finalidade (o resultado que se pretende obter) como efeito, a maneira como falamos parece inverter o sentido da relação causal — por exemplo, quando se diz “estou a estudar por causa do teste de amanhã”, é a finalidade que parece ser a causa e a acção que parece ser o efeito. Esta inversão confronta-nos com uma situação em que o efeito parece anteceder a causa, o que fere a noção comum de causalidade. Ver causa e efeito. (António Paulo Costa)
finitude e infinitude
Par de conceitos opostos que são usados em contextos filosóficos muito diversos. Os filósofos gregos usaram-nos para pensar a realidade, associando finitude a acabado e perfeito, e infìnitude a indeterminado e imperfeito. Com os primeiros pensadores cristãos, as polarizações inverteram-se e estes conceitos passaram a servir para pensar a relação do homem, entendido como finito, limitado ou imperfeito, com o divino, entendido como infinito, ilimitado ou perfeito, e embora mais recentemente alguns pensadores contemporâneos, como Heidegger e Sartre, tenham posto em causa o segundo pólo desta relação, ela continua a ser importante na filosofia da religião. Ver deus, imanente e transcendente. (Álvaro Nunes)
fisicismo
Teoria segundo a qual tudo o que existe tem uma natureza física. O fisicista sustenta que todos os estados ou mudanças do mundo são apenas estados ou mudanças de matéria e energia; e defende que aquilo que existe possui apenas propriedades físicas, como a forma, a dimensão, a carga eléctrica ou o estado de movimento. Se for verdadeira, a teoria tem consequências para a discussão do problema da relação entre o corpo e a mente: os acontecimentos mentais, exemplificados por sentimentos de dor, tristeza, entusiasmo, esperança, etc., nada mais serão do que eventos físicos ou, mais precisamente, acontecimentos cerebrais e neurofisiológicos. Recusando o dualismo entre o corpo e a mente, o fisicismo é, a par com o idealismo, uma das mais influentes doutrinas monistas. Várias versões de fisicismo foram defendidas ao longo da história, por exemplo, por Demócrito de Abdera (460 a.C.-370 a.C.), Thomas Hobbes ou W. v. O. Quine. Ver propriedade e dualismo e monismo. (António Paulo Costa)
forma lógica
Não é possível definir explicitamente a noção de forma lógica, mas pode-se dar exemplos claros: é evidente que há algo de comum às seguintes afirmações: “Se Deus existe, então a vida não faz sentido” e “Se Sócrates era ateniense, então não era alemão”. O que as duas frases têm de comum pode-se explicitar usando símbolos: Se P, então Q. Quando se substitui P por “Deus existe” e Q por “a vida não faz sentido” obtém-se a primeira afirmação. Quando se substitui P por “Sócrates era ateniense” e Q por “Sócrates não era alemão” obtém-se a segunda (que eliminou a repetição desnecessária da palavra “Sócrates”). Esta é a forma lógica mais superficial de afirmações muito simples, sendo suficiente para determinar a validade de certos tipos de argumentos, como o modus tollens e o modus ponens, por exemplo. A forma lógica de muitas afirmações é objecto de intensa discussão filosófica. (Desidério Murcho)
forma significante
As propriedades formais, comuns a todas as obras de arte, e só a elas, que provocam em nós emoções estéticas (ver emoção estética). Segundo o filósofo e crítico de arte Clive Bell (1881–1964) um objecto desperta em nós emoções estéticas se, e só se, tiver forma significante. Defende, assim, uma teoria formalista da arte (ver formalismo estético). Não se trata simplesmente de afirmar que as obras de arte têm uma forma, porque isso muitas coisas que não são arte têm. A forma significante consiste, no caso da pintura, numa certa combinação de linhas e cores; no caso da música, numa determinada organização temporal dos sons, etc. Falamos de forma significante quando referimos aspectos como a harmonia, o equilíbrio, a proporção, a elegância, etc. De acordo com a teoria da forma significante, é irrelevante se uma obra representa alguma coisa e qual a intenção do artista que a criou, pois o que conta são as suas propriedades internas. (Aires Almeida)
formal, lógica
Ver lógica formal.
formalismo estético
Doutrina segundo a qual apenas as características formais de uma obra fazem dela uma obra de arte e que as obras de arte devem ser avaliadas apenas em função de tais características. Como características formais costumam ser referidas a harmonia, o equilíbrio, a proporção, a elegância, a simplicidade, a complexidade, a unidade, o ritmo, etc. As teorias formalistas opõem-se geralmente às teorias da imitação e da expressão. O que importa, para o formalista, não é aquilo que está a ser imitado (nem o virtuosismo da imitação) e também não interessam os sentimentos supostamente expressos pelo artista (ou sentidos pelo espectador), visto que esses são critérios exteriores às próprias obras. Para o formalista só as propriedades intrínsecas da obra contam. Muitos artistas tinham como ideal esta concepção da arte, como os compositores do período clássico (Mozart e Haydn), ou os pintores neo-clássicos (Ingres e Jacques Louis David). Em filosofia da arte, as teorias de Clive Bell (1881–1964) e do célebre crítico musical Eduard Hanslick (1825–1904), são teorias formalistas. Também o esteticismo de Walter Pater (1839-94) e Oscar Wilde (1854–1900) é normalmente associado ao formalismo estético. Ver também forma significante. (Aires Almeida)
Foucault, Michel
(1926-84) Filósofo francês, Foucault é autor de uma obra desconcertante, que se situa entre a filosofia, a psicanálíse, a história e a linguística de maneira pouco convencional. Professor no Collège de France, as suas aulas intencionalmente obscuras trouxeram-lhe a fama de filósofo carismático. A sua investigação atravessa duas fases distintas. A primeira, conhecida como arqueológica, procura determinar as origens de práticas, teorias e instituições específicas. Na obra Loucura e Civilização (1961), por exemplo, Foucault tenta mostrar que o asilo teria sido uma instituição destinada a ocultar a relação perturbadora entre razão e loucura, que constituiria assim a “camada subterrânea” sobre a qual teria sido construído. A segunda fase consiste numa análise crítica das formas de exclusão social e cultural. Em Vigiar e Punir (1975), por exemplo, defende que a prisão moderna não resulta, como se pretende, do desejo de tratar os delinquentes de maneira mais humana, mas da intenção de dominar com eficácia indivíduos que ameaçam os poderes sociais e políticos. Este é apenas um caso da tese geral de que o conhecimento e o discurso humanista legitimam o poder instituído. A investigação de Foucault tem o objectivo de desafiar as divisões mais importantes de toda a nossa cultura: a divisão entre bem e mal, verdadeiro e falso (ver verdade e falsidade), normal e patológico. Talvez isso explique que, para os seus admiradores, Foucault seja uma espécie de herói cultural. Ver também estruturalismo. (Faustino Vaz)
Foucault, Michel, A Arqueologia do Saber (Coimbra: Almedina, 2005)
Foucault, Michel, As Palavras e as Coisas (Lisboa: Edições 70, 2002)
Foucault, Michel, História da Sexualidade, vols. I, II e III (Lisboa: Relógio d'Água, 1994)
frase
Uma sequência de palavras susceptíveis de serem usadas para fazer uma asserção ou uma pergunta, dar uma ordem ou exprimir um desejo. Um conjunto de palavras como “Se a neve é” não é uma frase. Uma frase interrogativa faz uma pergunta (“Será que Deus existe?”), uma frase imperativa dá uma ordem (“Não te atrevas a discordar de Kant!”), uma frase declarativa faz uma afirmação (“O aborto devia ser totalmente proibido”). Só as frases declarativas exprimem proposições, mas nem todas as frases declarativas exprimem proposições; uma frase declarativa como “As ideias verdes dormem furiosamente juntas” não exprime qualquer proposição. Não se deve confundir frase com proposição. (Desidério Murcho)
Frege, Gottlob (1848–1925)
Matemático, lógico e filósofo da linguagem, da matemática e da lógica alemão. Revolucionou a lógica, sendo consensualmente considerado o fundador da lógica moderna e posto a par de Aristóteles como um dos grandes nomes da história da disciplina.
Enquanto lógico, o seu objectivo básico foi a criação de um sistema formal no qual as demonstrações matemáticas pudessem ser rigorosamente formuladas, tornando explícitos todos os seus passos e permitindo assim a máxima clareza na justificação da sua validade (ou na exposição da sua invalidade). O seu inovador sistema permitiu pela primeira vez representar de modo sistemático relações lógicas que a forma gramatical das frases da linguagem corrente muitas vezes oculta. Por exemplo, Frege tornou popular a ideia de que a forma lógica de uma frase como “Todos os homens são mortais” esconde uma condicional (“Tome-se qualquer objecto; se esse objecto for um homem, então é mortal”). As inovações contidas na lógica de Frege perduraram até hoje e são os traços fundamentais da chamada “lógica clássica" (ver cálculo proposicional, cálculo de predicados, lógica), a qual substituiu com vantagem a lógica aristotélica como cânone da disciplina. As vantagens da substituição advêm não só do maior rigor do sistema de Frege mas também do seu maior poder expressivo. Com o sistema de Frege é possível, por exemplo, representar a forma lógica de afirmações como “se estiver a chover, nenhum estudante comparecerá” e “qualquer rapariga ama um actor americano”. O sistema permite, entre outras coisas, desfazer a ambiguidade de âmbito dos quantificadores de que esta última é um exemplo (a frase tem quer o significado de “qualquer rapariga ama um actor americano qualquer” quer o de “há um actor americano que todas as raparigas amam”).
Frege foi igualmente importante como filósofo da linguagem. Vale a pena notar que os princípios semânticos associados à sua lógica podem ser usados no estudo sistemático da linguagem corrente. Em particular, a sua distinção entre sentido e referência influenciou decisivamente não só a filosofia da linguagem posterior mas também a linguística moderna (ver semântica). Para Frege, as proposições ou “pensamentos” são entidades autónomas e objectivamente apreensíveis (uma concepção muitas vezes designada de “platonismo”, ver Platão) e não conteúdos psicológicos subjectivos e incomunicáveis. Em coerência com esta tese, também em filosofia da lógica Frege era anti-psicologista; e o seu anti-psicologismo nesta área determinou o modo como as leis da lógica passaram a ser canonicamente vistas: já não enquanto descrições do modo como os seres humanos de facto raciocinam, mas como princípios ilustrativos do modo como eles devem raciocinar para que os seus argumentos sejam válidos. Ver também cálculo proposicional, cálculo de predicados, lógica, lógica clássica. (Pedro Santos)
Frege, Gottlob, Fundamentos da Aritmética (Lisboa: INCM, 1992).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 21 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 14 (Lisboa: Presença, 1989).
função de verdade
Ver operador verofuncional.
funcionalismo estético
Perspectiva segundo a qual a arte tem uma função, servindo algum propósito ou finalidade. O funcionalismo estético, também chamado “instrumentalismo estético”, opõe-se assim ao esteticismo. A ideia de que a arte é um meio privilegiado para atingir certos fins considerados importantes é que justifica, de acordo com o funcionalista, o valor que lhe damos. Dependendo do tipo de função atribuída à arte, assim também podemos encontrar teorias funcionalistas diferentes: para uns, como o alemão Theodor Adorno (1903-69), tem uma função social; para outros, como o escritor russo Leão Tolstoi (1828–1910), tem uma função moral; para outros ainda, como o americano Nelson Goodman, a arte serve para aumentar o conhecimento. Ver também cognitivismo estético. (Aires Almeida)
fundacionalismo
Perspectiva epistemológica (ver epistemologia), segundo a qual as nossas crenças se apoiam num número reduzido de crenças mais básicas que servem de fundamento a todo o conhecimento. A ideia pode ser melhor compreendida a partir da conhecida metáfora de descartes que descreve o conhecimento como um edifício que precisa de se apoiar em alicerces sólidos. Tais alicerces têm de ser formados por um tipo diferente de crenças, cuja evidência seja indisputável. Assim, o fundacionalismo constitui uma perspectiva acerca do modo como se estrutura a justificação do nosso conhecimento. Quando pensamos no modo como justificamos a maior parte das nossas crenças, verificamos que o fazemos recorrendo a outras crenças que nos parecem mais evidentes do que as anteriores. Mas estas crenças precisam, por sua vez, de ser justificadas com outras crenças ainda mais evidentes, e assim sucessivamente, a não ser que se disponha de um conjunto limitado de crenças fundamentais e completamente evidentes, que bloqueiem o risco de regressão ao infinito. O fundacionalismo constitui, por isso mesmo, uma resposta às dúvidas dos cépticos (ver cepticismo) acerca da possibilidade de justificar satisfatoriamente as nossas crenças e opõe-se ao coerentismo, segundo o qual as nossas crenças se apoiam mutuamente entre si, sem qualquer necessidade de recorrer a qualquer tipo de crenças que lhes sirvam de fundamento. É de salientar que as crenças fundamentais exigidas pelo fundacionalista tanto podem ser de natureza empírica, apelando assim para um tipo de evidência sensível (ver empirismo), como de carácter racional, apelando para uma evidência de tipo racional (ver racionalismo). (Aires Almeida)
G
Galileu Galilei (1564–1642)
Cientista e filósofo italiano. Foi julgado por defender o heliocentrismo sobretudo no seu Diálogo dos Grandes Sistemas (1632; trad. 1980, Gradiva), o que nessa época se opunha à doutrina oficial da igreja, ao senso comum e à autoridade de Aristóteles. Acabou por ser condenado a prisão domiciliária e morreu cego. As suas ideias acerca do método científico, assim como os resultados práticos da sua aplicação, deram origem à ciência moderna. Tais ideias conduziram também ao abandono de uma concepção da natureza herdada de Aristóteles e com mais de dois mil anos de tradição. Esta foi a razão pela qual Galileu travou uma intensa luta contra os argumentos de autoridade em que se refugiavam os académicos de então, batendo-se pela autonomia da ciência e pela investigação directa e metódica da natureza. Defendeu a aplicação da matemática na explicação dos fenómenos naturais, o que fez pela primeira vez em relação ao movimento, e que se tornou uma característica fundamental da ciência. A sua concepção mecanicista (ver mecanicismo) da natureza articulava-se com a posição epistemológica do realismo crítico e com a ideia de que as características que observamos nos objectos se dividem em qualidades primárias e qualidades secundárias. (Aires Almeida)
Geist
Termo alemão que significa “alma” ou “espírito”. Ver Hegel.
generalização
Um tipo muito comum de inferência indutiva (ver indução), que estabelece uma conclusão geral como, por exemplo, “os portugueses são machistas” a partir de casos menos gerais. Atribui-se assim a mesma propriedade, a propriedade de ser machista, a uma certa classe de indivíduos ou objectos, a classe dos portugueses. Apesar de o raciocínio indutivo não se fazer apenas por generalização, grande parte do raciocínio comum é desse tipo. (Aires Almeida)
génio maligno
Hipótese introduzida por Descartes com o fim de dramatizar os argumentos cépticos contra a ideia de que sabemos seja o que for, convidando-nos a imaginar que os nossos pensamentos e percepções estão sistematicamente a ser manipulados por uma espécie de Deus enganador. Claro que, sendo enganador, não poderia ser bom e, portanto também não poderia ser Deus, dado que a bondade é uma das características de Deus. Daí dizer que se trata de um génio maligno. O poder desse génio faria com que nos enganássemos de tal modo que tomássemos sempre como verdadeiro aquilo que não passa, afinal, de meras ilusões. Esta hipótese é rejeitada pelo próprio Descartes, concluindo que de uma coisa tal génio não o pode enganar: que existe, dado que está a ser enganado por ele. Uma versão mais actual da hipótese do génio maligno é a experiência mental do “cérebro numa cuba”, apresentada pelo filósofo americano Hilary Putnam (n. 1926). O filme The Matrix parte da mesma ideia. (Aires Almeida)
Gestalt
Termo alemão que significa “configuração”. Foi introduzido na psicologia cognitiva para designar o facto de a percepção de objectos não se dar em termos atómicos, objecto a objecto, como até então era comum supor-se, mas antes em termos de grandes configurações ou grupos de percepções. Wittgenstein foi influenciado por estas teorias, tendo defendido, na obra Investigações Filosóficas, uma teoria do significado “gestaltista”, por oposição à sua própria anterior teoria pictórica do significado, que era atomista. (Desidério Murcho)
gnosiologia
O mesmo que teoria do conhecimento, ou também epistemologia. Alguns filósofos utilizam este termo de origem latina para se referirem ao conjunto de conceitos e de problemas acerca do conhecimento. (Aires Almeida)
gnothi se auton
Expressão grega que significa “conhece-te a ti mesmo”. Inscrita no pórtico de Delfos, na Grécia antiga, Sócrates declarou ter dedicado a sua vida ao auto-conhecimento. Deste modo, Sócrates parecia conceber a filosofia como uma actividade prática, que envolvia todo o ser humano, e não apenas os aspectos teóricos do conhecimento. Aristóteles partilhava a mesma perspectiva, mas mais por considerar que nenhuma actividade de investigação racional nos é estranha enquanto seres humanos, pois somos seres racionais. (Desidério Murcho)
Gödel, Kurt
(1906–1978) Lógico e filósofo norte-americano de origem austríaca. O que o tornou célebre foram certos resultados da lógica, nomeadamente o seu teorema da incompletude, publicado em 1931. Este teorema mostra que em certos sistemas de lógica clássica suficientemente fortes para incluírem a aritmética, haverá sempre proposições verdadeiras que não se pode provar nesse sistema que são verdadeiras. (Hoje em dia podemos construir sistemas lógicos que incluem a aritmética e que não padecem desta limitação.) Abundam as interpretações erradas do seu resultado, pensando-se muitas vezes que constitui uma demonstração dos limites da razão. Pelo contrário, Gödel encarava o seu resultado como a demonstração de que nem mesmo a racionalidade matemática se pode reduzir à mera manipulação cega de símbolos, o que por sua vez significava que a concepção empirista da racionalidade estava errada. Gödel apresentou também uma versão do argumento ontológico, baseando-se em conceitos centrais de Leibniz. (Desidério Murcho)
Goodman, Nelson (1906–1998)
Filósofo americano. Conhecido sobretudo pelo seu trabalho relativo ao problema da indução, as suas ideias abrangem também temas da metafísica e da filosofia da arte.
Relativamente ao problema da indução, Goodman apresenta em Facto, Ficção e Previsão (1954; trad. 1991, Presença) o famoso Novo Enigma da Indução que procura mostrar que este problema não depende unicamente da relação de confirmação mas também da adequação dos predicados usados para fazer induções.
Na metafísica, Goodman defendeu, em Modos de Fazer Mundos (1978; trad. 1995, Asa), uma versão extrema de idealismo, segundo a qual só há inúmeras versões diferentes de “mundos”, não existindo um mundo independente das nossas representações.
Na filosofia da arte, defendeu, em Linguagens da Arte (1976; trad. 2003, Gradiva), uma versão sofisticada da teoria institucional da arte, o valor cognitivo da arte e o artificialismo da distinção entre artes e ciências.
Partindo do positivismo lógico, aceita algumas das ideias centrais deste movimento, como o nominalismo (a crença de que não há universais, como a brancura), rejeita outras (como a suposta superioridade da ciência na tarefa de conhecer o mundo) e abraça algumas das consequências mais polémicas desse movimento (o extremo anti-realismo, que declara ser tudo uma construção linguística). (Desidério Murcho)
gosto, padrão de
Ver padrão de gosto.
gosto, teoria do
Ver teoria do gosto.
H
Hare, R. M. (1919-2002)
Filósofo inglês que exerceu uma grande influência na ética. No domínio da metaética, Hare rejeitou o realismo moral, mas, influenciado por Kant, defendeu a racionalidade e objectividade do pensamento ético propondo o prescritivismo universal. De acordo com esta perspectiva, os juízos morais não são simples descrições de factos, pois parte do seu significado é irredutivelmente prescritivo ou normativo (ver normativo e descritivo). Por exemplo, quem afirma “Deves dizer a verdade” ou “Não dizer a verdade é errado”, está a dizer algo como “Diz a verdade!”. No entanto, as prescrições morais não são arbitrárias, pois têm de ser universalizáveis — quando prescrevemos moralmente que alguém diga a verdade, estamos a prescrever que todas as pessoas em circunstâncias semelhantes nos aspectos relevantes digam a verdade. Hare sustentou que esta maneira de conceber os juízos morais conduz a uma versão de utilitarismo segundo a qual devemos satisfazer tanto quanto possível os desejos ou preferências dos que poderão ser afectados pela nossa conduta. Entre as suas obras mais importantes contam-se Moral Thinking (1981) e Sorting Out Ethics (1997). Ver imperativo categórico, Singer. (Pedro Galvão)
hedonismo
Doutrina segundo a qual o prazer é o único verdadeiro bem. Há três tipos de hedonismo: o psicológico, que sustenta que as pessoas procuram inevitavelmente o prazer; o ético (ver ética), que considera que a obrigação dos seres humanos é procurar o prazer; e o reflexivo, que afirma que aquilo que dá valor a qualquer ocupação é o prazer. Nalgumas teorias consequencialistas, como o utilitarismo de Jeremy Bentham (1748–1832) e de John Stuart Mill, o prazer constitui o critério para julgar as acções. Na Antiguidade, o hedonismo está sobretudo associado aos Cirenaicos e aos Epicuristas. Ver epicurismo. (Álvaro Nunes)
Hegel, Georg Wilhelm (1770–1831)
Pensador alemão que atribui à filosofia a tarefa de ultrapassar concepções dualistas e parciais da realidade em nome do princípio de que “a verdade é o todo”. Para a filosofia ser “sistema do Absoluto" importa negar a separação entre o Infinito (Espírito absoluto) e o finito (o mundo e o homem). Para tal, o Absoluto assume a condição finita, primeiro na Natureza e depois na História humana. Ultrapassando cada forma espaciotemporalmente limitada da sua odisseia histórica, o Absoluto transforma o finito em momento da sua vida infinita, em auto-limitação momentânea. Nada existe ou é verdadeiro fora do Absoluto. A filosofia é a forma superior de exposição do movimento dialéctico mediante o qual o Espírito divino se diz absoluto ao negar que o finito exista fora de si. Ser absoluto é fazer-se absoluto. Na Fenomenologia do Espírito e em A Razão na História (trad. 1995, Edições 70), entre outras obras, é exposta esta visão do Espírito como auto-realização. (Luís Rodrigues)
Heidegger, Martin (1889–1976)
Filósofo alemão, cuja reflexão, centrando-se na questão do sentido do ser, desenvolve essencialmente um tema: o esquecimento ou olvido do Ser. Acusa a filosofia ocidental de, a partir de Platão, ter esquecido o sentido original do Ser: para os primeiros filósofos gregos o Ser era desocultação, luz e abertura que torna possível que as coisas (os entes) sejam ditas e pensadas. Não sendo um ente, não sendo isto ou aquilo, o Ser manifesta-se em todos os entes ocultando-se. Esquecendo a diferença ontológica (a diferença Ser-ente) e o sentido original do Ser, a metafísica ocidental concebeu este como a causa ou a explicação da totalidade dos entes. Na maioria dos casos, a causa dos entes seria Deus, o ente supremo. Preocupada com a explicação dos entes, a metafísica ocidental desenvolveu uma concepção instrumental do Ser reduzindo-o a entidade que produz ou causa algo quando o que o Ser faz é “deixar ser” o ente. O momento culminante de tal concepção é a transformação dos entes em objectos a manipular, consumir e explorar. A principal consequência do olvido do Ser é a submissão do mundo e da natureza aos imperativos da técnica. Em Sobre a Essência da Verdade (1943; trad. 2001, Porto Editora), O Que é a Metafísica? (1929) e A Questão da Técnica (1949), por exemplo, são expostas estas ideias. (Luís Rodrigues)
hermenêutica
Originalmente, teoria ou método de interpretação da Bíblia e de outros textos religiosos. Friedrich Schleiermacher (1768–1834) formulou uma teoria da interpretação dos textos e do discurso, que Wilhelm Dilthey (1833–1911) aplicou a todos os actos e produtos humanos e Heidegger estendeu ao ser humano (Dasein). Associada à hermenêutica está a ideia de círculo hermenêutico: não podemos compreender completamente um todo (por exemplo, um texto filosófico) a menos que entendamos as suas partes, ou completamente as partes a menos que entendamos o todo. Heidegger e Hans-Georg Gadamer (1900–2002) fizeram disto uma característica de todo o conhecimento e actividades humanos. Ver interpretação. (Álvaro Nunes)
heteronomia
Ver autonomia e heteronomia.
hipotética, proposição
Ver proposição hipotética.
história da filosofia
Ver filosofia, história da.
Hobbes, Thomas (1588–1679)
Filósofo inglês. Na sua obra mais influente, Leviatã (1650; trad. 1995, Imprensa Nacional), Hobbes propôs uma visão materialista do universo e da natureza humana (ver fisicismo), advogou o determinismo e apresentou uma teoria contratualista para justificar o poder político do soberano. O seu contratualismo parte da ideia de estado da natureza. Nessa condição, não há qualquer poder político e os seres humanos, tendo uma força aproximadamente igual, vivem numa permanente guerra de todos contra todos. Para ultrapassar este estado de coisas, sustentou Hobbes, precisamos de concordar ser governados por um monarca com poder absoluto, pois só ele será capaz de garantir uma coexistência pacífica. (Pedro Galvão)
holismo
A ideia de que o todo tem prioridade sobre as partes. Na filosofia da ciência, a perspectiva segundo a qual as diversas hipóteses que constituem uma teoria científica não podem ser testadas uma a uma. Testar uma teoria científica implica confrontá-la com a observação. Para fazer isso é preciso deduzir (ver dedução) da teoria certas previsões observacionais. O holista sustenta que não se pode deduzir tais previsões de hipóteses isoladas — na verdade, deduz-se a previsão de todo um conjunto bastante vasto de hipóteses. Assim, se a previsão fracassar tudo o que podemos inferir é que pelo menos uma dessas hipóteses é falsa — não podemos concluir que uma certa hipótese específica foi refutada. Esta perspectiva, também conhecida por tese de Duhem-Quine, sugere que não é fácil falsificar conclusivamente hipóteses científicas. Em epistemologia o coerentismo é um exemplo de holismo. Ver falsificacionismo, método científico. (Pedro Galvão)
homem de palha, falácia do
Ver falácia do homem de palha.
Hume, David (1711–76)
Filósofo, ensaísta e historiador escocês, pertence à tradição empirista britânica, cujos antecessores foram Locke e Berkeley. É talvez o primeiro filósofo a procurar trazer para a filosofia o tipo de atitude que tantos resultados produziu nas ciências da natureza do seu tempo. Ficou famoso o seu conselho de que devemos deitar à fogueira tudo o que não for ciência empírica ou disciplinas matemáticas. Este tipo de atitude voltaria a ser popular, sobretudo junto dos filósofos do positivismo lógico. Para não correr o risco de ser ele próprio deitado à fogueira, pelo menos metaforicamente, só permitiu que os Diálogos sobre a Religião Natural (1779) fossem publicados depois da sua morte. Nesta obra, Hume apresenta uma análise hoje clássica dos argumentos contra e a favor da existência de Deus. O seu argumento contra os milagres foi exposto também no Ensaio sobre o Entendimento Humano.
A sua primeira obra, o Tratado da Natureza Humana (1739-40), procura ambiciosamente estabelecer os fundamentos de uma teoria empírica da natureza humana. Nesta obra encontram-se algumas das ideias que mudaram a face da filosofia moderna, nomeadamente no que respeita à epistemologia e à ética. Porque os seus contemporâneos não lhe prestaram grande atenção, Hume tentou apresentar aproximadamente as mesmas ideias, de forma mais clara, nas obras Investigação sobre o Entendimento Humano (1748) e Investigação sobre os Princípios da Moral (1751).
No que respeita à epistemologia, Hume introduz de forma clara a distinção entre conhecimento a priori e a posteriori, a que ele chamou, respectivamente, “relações de ideias” e “questões de facto”. O conhecimento a priori tem por objecto unicamente as matemáticas; todo o conhecimento do mundo é baseado na experiência, não sendo possível estabelecer a priori nem mesmo os princípios mais gerais que regulam as verdades empíricas, como o princípio de causalidade. A teoria da causalidade de Hume baseia-se na projecção psicológica: perante sucessões repetidas de acontecimentos do mesmo tipo, os seres humanos são levados a inferir fantasiosamente a existência de uma conexão causal entre esses acontecimentos.
Hume adopta a mesma estratégia projectivista em ética. Traçando uma distinção profunda entre factos e valores, declara que não se podem extrair os últimos dos primeiros, e que a ética é apenas o resultado da projecção de valores humanos sobre os factos do mundo, valores estes ancorados no sentimento e não na razão. O seu argumento baseia-se na ideia de que os factos são objecto de crença e que as crenças não são motivadoras, isto é, não têm o poder de nos levar a agir; só os desejos têm esse poder. Tanto no âmbito da epistemologia como da ética, as ideias de Hume foram das mais influentes de sempre na história da filosofia. (Desidério Murcho)
Hume, David, Investigação sobre os Princípios da Moral (Lisboa: INCM, no prelo).
Hume, David, Obras de Filosofia da Religião (Lisboa: Fundação Calouste Gulbenkian, no prelo).
Hume, David, Tratado da Natureza Humana (Lisboa: Fundação Calouste Gulbenkian, 2002).
Hume, David, Investigação sobre o Entendimento Humano (Lisboa: INCM, 2002).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 14 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 7 (Lisboa, Presença, 1989).
Husserl, Edmund (1859–1938)
Filósofo e matemático alemão fundador da fenomenologia, a corrente filosófica cujo objectivo era transformar a filosofia numa ciência rigorosa, mediante a descrição do modo como as coisas surgem na consciência, independentemente de quaisquer pressupostos teóricos ou metafísicos. A ideia central é a de descrever os fenómenos (ver fenómeno) na sua pureza; descrever o que aparece na consciência, suspendendo as nossas crenças de senso comum sobre a natureza e até sobre a existência de objectos exteriores. Esta atitude opõe-se à “atitude natural”, pois trata-se de “pôr entre parênteses" tudo o que vai além da experiência subjectiva. Há, assim, uma “redução fenomenológica" — uma redução aos fenómenos, também chamada epochê — através da qual seja possível fazer uma descrição rigorosa e objectiva do conteúdo da consciência; o que interessa para a fenomenologia não são as coisas do mundo e muito menos saber se os conteúdos da consciência correspondem a algo real ou irreal no mundo exterior. A fenomenologia é, assim, caracterizada como uma ciência da consciência, que se demarca quer do naturalismo, ao exigir a suspensão de quaisquer crenças acerca do mundo exterior e dispensar os dados empíricos nos quais elas se baseiam, quer do psicologismo, dado o seu alegado carácter rigoroso e obejctivo. Neste aspecto, a fenomenologia de Husserl aproxima-se, por um lado, do subjectivismo cartesiano (ver Descartes) e, por outro lado, do idealismo transcendental de Kant. Outra das ideias centrais da fenomenologia de Husserl deve-se ao filósofo austríaco Franz Brentano — de quem Husserl foi aluno em Viena e que o fez interessar-se decisivamente pela filosofia. Trata-se da ideia de intencionalidade: toda a consciência é consciência de algo, sendo este um dos factos mais importantes acerca dos nossos conteúdos mentais. A filosofia é considerada por Husserl como uma ciência de rigor porque se atém ao essencial — a experiência da consciência — afastando-se da atitude natural e de todo o tipo de preconceitos e de interesses práticos ou teóricos que lhes estão associados. Isto consegue-se não através da indução nem na dedução, mas da redução, que constitui o método desta ciência de rigor. A fenomenologia de Husserl influenciou muitos filósofos, entre os quais se contam Heidegger, Merleau-Ponty, Sartre, Gadamer e Lévinas, sendo, por isso, um dos mais influentes filósofos do séc. XX. As suas obras mais importantes são Investigações Lógicas (1900–01), Ideias Directrizes para uma Pura Fenomenologia e para uma Filosofia Fenomenológica (1913) e Meditações Cartesianas (1931). (Aires Almeida)
hylê
Termo grego que significa “substrato” ou “matéria”. Aristóteles usava o termo para falar do que permanece para lá da mudança: quando se faz uma estátua de um pedaço de barro, por exemplo, muda a forma, mas não a matéria ou substrato. Berkeley chamou Hilas a uma das personagens dos seus Diálogos — o defensor da teoria aristotélica da existência da matéria. Husserl usou o mesmo termo para falar do tipo de experiências perceptivas que podem ser enganadoras, como quando parece que vemos uma pessoa à distância e afinal era um boneco. (Desidério Murcho)
I
idealismo
Vulgarmente diz-se que uma pessoa é idealista quando se bate por ideais e orienta as suas acções em função deles. Mas o significado filosófico do termo é substancialmente diferente. Em filosofia chama-se “idealista” a qualquer doutrina que afirme que a natureza última da realidade é mental, opondo-se ao realismo. Isto tanto pode querer dizer que os objectos físicos não existem a não ser como objectos para uma mente, ou que são apenas conteúdos mentais, ou que são algo intrínseca e essencialmente mental. O fundador do idealismo foi o filósofo irlandês George Berkeley para quem só existem dois tipos de coisas: mentes e ideias. Os chamados “objectos físicos” não passam, de acordo com Berkeley, de impressões do sujeito capaz de sentir. Assim, a maçã que temos diante de nós é apenas o conjunto das sensações de cor, sabor, odor, forma, textura, etc., que estão perante a nossa mente quando a percepcionamos. Daí a célebre afirmação de Berkeley de que o seu esse (existência) é percipi (ser percepcionada), o que equivale a dizer que só as sensações são reais. Mas as sensações nada mais são, segundo Berkeley, do que conteúdos mentais ou ideias. Daí o nome “idealismo” e a conclusão de que os objectos não existem fora de alguma mente que os percepcione. O idealismo de Berkeley tem um cariz marcadamente ontológico (ver ontologia), na medida em que defende que toda a realidade é mental. Outra forma de idealismo, de pendor mais epistemológico (ver epistemologia), é o chamado “idealismo transcendental” de Kant. Kant admite a existência de uma realidade independente da mente, mas afirma que dela nada podemos saber. É idealista na medida em que defende que o mundo tal como o conhecemos é o produto das leis que o sujeito impõe aos objectos quando os percepciona. Os objectos da experiência não são, assim, entidades independentes. Essas leis fazem parte do que Kant designa como “estrutura transcendental” do sujeito. Daí o nome por que é conhecido este tipo de idealismo. Há ainda um terceiro tipo de idealismo, o idealismo absoluto, defendido por Fichte (1762–1814), e sobretudo por Hegel. Para Hegel toda a realidade é expressão do Espírito Absoluto, que toma consciência de si exteriorizando-se e manifestando-se nos objectos físicos. Aquilo a que chamamos “realidade exterior” é a expressão concreta de uma entidade espiritual única e universal. (Aires Almeida)
ideia
O termo tanto pode, como em Platão, designar realidades objectivas, inteligíveis (ver inteligível), eternas, imutáveis e transcendentes (ver transcendente), que são modelos e causas do mundo sensível, como, sobretudo a partir do séc. XVII com Descartes, Locke, Berkeley e Hume, designar quaisquer conteúdos mentais subjectivos (percepções, recordações, sonhos, pensamentos), que são vistos frequentemente como representações (ver representação) dos objectos do mundo exterior. Isto origina vários problemas interessantes, como o de saber se as ideias são representações adequadas da realidade ou se conhecemos alguma coisa para além das ideias. (Álvaro Nunes)
ideias inatas
Conteúdos mentais anteriores a qualquer experiência e que dela são independentes. Trata-se de ideias com as quais já nascemos e que, portanto, não são adquiridas. Descartes deu o exemplo das ideias de Deus, de infinito, de imortalidade e de perfeição, as quais defendia que nada de empiricamente observável pode ter originado. Estas ideias constituem, alegadamente, um tipo de conhecimento que veio a chamar-se conhecimento a priori. A existência ou não de ideias inatas esteve no centro das disputas entre o racionalismo e o empirismo. Empiristas como Locke e Hume opõem-se à afirmação de que há ideias inatas ou conhecimentos a priori. Kant defende que há noções a priori, mas que tais noções são apenas formais, não podendo, só por si, ser consideradas conhecimento. Mas hoje em dia a discussão entre empiristas e racionalistas não se foca em torno desse aspecto, mas em torno do a priori. O conhecimento a priori é diferente do conhecimento inato: o primeiro é aquele que adquirimos pelo pensamento apenas, o segundo não é adquirido, nascemos com ele. (Aires Almeida)
identidade
Uma afirmação como “Sócrates é Platão” exprime uma identidade — falsa, neste caso. Uma identidade com a forma lógica “m = n” só é verdadeira caso os nomes simbolizados por m e n denotem o mesmo particular: “Véspero é Vénus” exprime uma identidade verdadeira porque os dois nomes denotam o mesmo particular. Chama-se “numérica” a esta identidade, que só ocorre entre um particular e ele próprio. Assim, qualquer frase com a forma “n = n” é logicamente verdadeira. Chama-se por vezes “princípio ou lei da identidade” a esta verdade lógica.
Distingue-se a identidade numérica da identidade qualitativa, que diz respeito à completa partilha de propriedades. Por exemplo, quando alguém diz que o António é igual ao Miguel, não está a dizer que eles são a mesma pessoa, mas que têm muitas características (ou propriedades) em comum. É um problema filosófico em aberto saber se dois objectos numericamente distintos podem todavia ser qualitativamente idênticos, isto é, se podem ter exactamente as mesmas propriedades.
Não se deve pensar que todas as frases como “F é G” exprimem identidades, pois podem também exprimir predicações: “Platão é alto” não exprime a identidade entre Platão e ser alto, mas antes a ideia de que Platão tem a propriedade de ser alto. Ver também ser. (Desidério Murcho)
identidade pessoal
As pessoas persistem no tempo: existem em muitos momentos diferentes. Por exemplo, é comum considerar-se que eu sou hoje a mesma pessoa que era quando tinha apenas dois anos de idade. Esta identidade aparente levanta contudo problemas filosóficos óbvios, pois não tenho hoje quase nenhuma das propriedades mais salientes que tinha aos dois meses. O que faz cada um de nós ser a mesma pessoa ao longo do tempo, apesar das mudanças físicas e psicológicas que se vão acumulando? Uma possibilidade é que a nossa identidade ao longo do tempo se deva essencialmente à continuidade corporal: ao facto de termos o mesmo corpo ao longo de toda a vida. Outra possibilidade é a identidade pessoal consistir apenas na continuidade psicológica: no facto de termos estados mentais (como memórias, intenções, crenças e planos) que se mantêm ao longo do tempo ou que se relacionam causalmente entre si. O que aconteceria, por exemplo, se o nosso corpo fosse destruído mas transplantassem o nosso cérebro para um novo corpo? Quem defende o critério da continuidade corporal dirá que morremos com a destruição do corpo. Quem defende o critério da continuidade psicológica afirma, pelo contrário, que poderíamos viver num novo corpo ou, talvez, até num suporte não biológico. Todas as teorias tradicionais enfrentam problemas espinhosos. No caso da continuidade psicológica, temos o chamado “problema da bifurcação”: a possibilidade teórica de criar réplicas co-ocorrentes da mesma pessoa, ambas em continuidade psicológica com o indivíduo original, o que levanta a pergunta, “Qual delas é o “verdadeiro" indivíduo?”. A teoria da continuidade do corpo enfrenta a objecção óbvia de que sobrevivemos a transformações qualitativas radicais nos nossos corpos. Ver identidade, tempo. (Pedro Galvão)
ignoratio elenchi
Expressão latina por que também é conhecida a falácia da conclusão irrelevante. Trata-se de um argumento em que se prova uma coisa diferente do que está em causa. Veja-se o argumento: “É através dos impostos que o governo arranja dinheiro para ajudar os cidadãos mais carenciados; mas, dado que ainda há muitas pessoas com carências, o governo deve aumentar os impostos”. Este argumento não prova o que pretende, ou seja, que as carências dos cidadãos se resolvam com a subida de impostos. Pode ser até que o aumento de impostos coloque em situação de carência algumas pessoas que não estavam nessa situação. (Aires Almeida)
igualdade
Na filosofia política, atribuir a máxima importância à igualdade é defender o igualitarismo — a perspectiva segundo a qual os bens sociais devem ser distribuídos tão equitativamente quanto possível (ver justiça). Advogar a igualdade de oportunidades é pensar que a posição que as pessoas ocupam na sociedade deve resultar de uma competição justa entre indivíduos. Em ética, usa-se frequentemente a noção de igualdade para exprimir a ideia de que todas as pessoas têm a mesma importância ou estatuto moral — na ética deontológica de Kant, sustenta-se que todos nós devemos ser tratados como fins em si (ver imperativo categórico), e os utilitaristas, como Hare ou Singer, afirmam que os interesses de qualquer pessoa (ou animal capaz de sofrer) merecem uma igual consideração. Nenhuma destas teorias morais implica o igualitarismo político. Ver Rawls, utilitarismo. (Pedro Galvão)
iluminismo
Movimento cultural que floresceu na Europa do séc. XVIII. A confiança resoluta na racionalidade humana é o traço mais saliente dos pensadores deste movimento. Os iluministas insurgiram-se contra o pensamento supersticioso associado à religião, advogaram a difusão do conhecimento científico e esforçaram-se por promover o progresso humano não só em questões teóricas, mas também em questões políticas e morais. Hume e Kant contam-se entre os filósofos iluministas mais influentes. (Pedro Galvão)
imanente
1. O que faz parte da própria natureza de uma coisa ou pessoa, como sua característica interna ou intrínseca. Opõe-se a transcendente, isto é, o que é exterior ou ultrapassa essa coisa ou pessoa.
2. O panteísmo concebe Deus como um ser imanente, pois identifica-o com o próprio mundo ou natureza. Pelo contrário, para o teísmo Deus é transcendente, pois é exterior ao mundo por si criado.
3. Diz-se que a crítica a uma teoria é imanente quando se apoia nas afirmações da própria teoria criticada. (Aires Almeida)
imediatez e mediação
São conceitos indispensáveis para a compreensão do pensamento de Hegel. A imediatez é a potencialidade, o estado do que ainda não se desenvolveu e actualizou. A mediação é a condição de actualização, aquilo sem o que uma coisa não se pode realizar. O mediato é o que está entre a apresentação imediata e incompleta de uma coisa e o momento da sua actualização completa. Na transição, ou devir, a negação desempenha um papel importante. A semente é a maçã sob a sua forma imediata (abstracta). Irá superar a sua imediatez transformando-se em flor e fruto, isto é, negando-se como semente. A maçã é resultado de um processo que nega mas conserva como necessários os momentos ultrapassados (a semente, a flor). (Luís Rodrigues)
imperativo categórico
Na ética deontológica de Kant, o imperativo categórico é o princípio ou lei moral fundamental. Tal princípio é categórico, por oposição a hipotético, porque se nos apresenta como uma obrigação absoluta ou incondicional. Kant pensava que, como conhecemos este princípio a priori (ver a priori e a posteriori), temos de o aceitar sejam quais forem os nossos desejos ou interesses particulares. Há várias maneiras de formular o imperativo categórico. Uma das fórmulas capta uma exigência de universalidade: “Age apenas segundo uma máxima tal que possas ao mesmo tempo querer que ela se torne uma lei universal”. Segundo esta fórmula, é errado agir segundo máximas que não possamos querer universalizar — se não podemos querer que todas as pessoas procedam de acordo com uma certa máxima, então nós próprios não a podemos adoptar. É errado, por exemplo, agir segundo a máxima “Faz promessas com a intenção de não as cumprires”, pois não podemos querer que todos adoptem esta máxima, já que se todos fizessem promessas com a intenção de as não cumprirem ninguém confiaria em ninguém e a própria prática de fazer promessas desapareceria. Outra fórmula do imperativo categórico exprime uma exigência de respeito: “Age de tal maneira que uses a tua humanidade, tanto na tua pessoa como na pessoa de qualquer outro, sempre e simultaneamente como fim e nunca simplesmente como meio”. Isto significa que é sempre errado tratar uma pessoa como se esta fosse um instrumento ao serviço dos nossos objectivos. Podemos dizer, utilizando o mesmo exemplo, que é errado fazer promessas com a intenção de as não cumprir porque quem procede assim trata os outros como simples meios para alcançar os seus objectivos. Ver dever, Hare, vontade boa. (Pedro Galvão)
implicação
Um conjunto C (possivelmente singular) de afirmações implica outra afirmação Q se Q for verdadeira em todas as circunstâncias em que as afirmações de C forem verdadeiras. Dá-se a esta relação muitas vezes também o nome de implicação lógica. Por exemplo, em qualquer circunstância em que as afirmações “Os tiranos corrompem” e “João é tirano” sejam verdadeiras, a afirmação “João corrompe” será também verdadeira, de modo que esta última é implicada pelas duas primeiras. A relação da implicação com a validade de um argumento (e portanto com a lógica) é directa: dada a definição acima, se as afirmações de C implicam Q, então existe um argumento válido com as afirmações de C como premissas e Q como conclusão (no exemplo, as duas primeiras afirmações seriam as premissas e a terceira a conclusão). A noção clássica de implicação (e portanto de validade lógica) tem sido contestada por alguns autores, que exigem que as afirmações se relacionem quanto ao seu conteúdo para que se possa dizer que estamos perante uma relação de implicação. Algo equivocamente, o termo “implicação” é, algumas vezes, utilizado como equivalente a “condicional”. Nesta acepção, usa-se muitas vezes a definição de condicional da lógica clássica para dizer que uma afirmação P implica outra Q se não é o caso de P ser verdadeira e Q falsa. A este tipo de implicação (mais fraca do que a implicação lógica) dá-se normalmente o nome de “implicação material”. (Pedro Santos)
implícita, definição
Ver definição implícita.
inatas, ideias
Ver ideias inatas.
incomensurabilidade
Propriedade de duas ou mais coisas não serem comparáveis. Na sua filosofia da ciência, Kuhn defende que os paradigmas são incomensuráveis. Para Kuhn, a história de qualquer disciplina cientificamente amadurecida consiste numa sucessão de paradigmas separados por revoluções científicas. Por exemplo, na física o paradigma aristotélico deu lugar ao paradigma newtoniano. Afirmar que estes paradigmas são incomensuráveis é dizer que não podemos comparar a física de Aristóteles com a física de Newton e concluir que, objectivamente, a segunda é melhor ou está mais próxima da verdade do que a primeira. Cada paradigma proporciona uma maneira de ver um mundo e, quando os cientistas mudam de paradigma, de certo modo mudam também de mundo. Nestas circunstâncias, não podemos avaliar os paradigmas à luz de padrões ou critérios que estejam acima de qualquer paradigma. Ver relativismo. (Pedro Galvão)
indeterminismo
Teoria que abrange várias concepções do mundo incompatíveis com o determinismo. Numa versão mais fraca do indeterminismo, salienta-se que algumas ocorrências no mundo, como aquelas que são estudadas pela física quântica, não são determinadas por estados anteriores. Numa versão mais forte, defende-se que nenhum estado do mundo é determinado por estados anteriores, sendo a causalidade uma mera ilusão. Se isto for verdade, levanta-se o problema da atribuição de responsabilidade aos agentes, dado que as suas acções serão aleatórias.
Será o indeterminismo compatível (ver compatibilismo e incompatibilismo) com o livre-arbítrio? Negando que qualquer acontecimento do mundo, incluindo as acções, seja causalmente determinado, não tem sentido dizer que a versão mais forte do indeterminismo é compatibilista, pois assume que o determinismo é falso. Mas a versão mais fraca do indeterminismo admite que alguns acontecimentos do mundo são determinados por causas. Assim, a teoria poderia ser considerada compatibilista se os indeterministas radicais incluíssem as acções no conjunto dos acontecimentos que são determinados por causas e argumentassem a favor da sua compatibilidade com o livre-arbítrio. Ver acção, agente, causa e efeito, relação causal, dilema de Hume. (António Paulo Costa)
indexical
Um termo cuja referência depende inteiramente do contexto de uso. Por exemplo: “amanhã”, “eu”, “aqui”, etc. A palavra “amanhã” refere o dia 22 de Julho, se for proferida no dia 21 de Julho; mas refere o dia 2 de Setembro, se for proferida no dia 1 de Setembro. Cada indexical tem uma regra de uso. Por exemplo, a regra do indexical “eu” é a seguinte: o termo “eu” numa frase e num dado contexto refere o locutor ou autor dessa frase nesse contexto; o termo “hoje” numa frase e num dado contexto refere o dia em que o locutor ou autor dessa frase e nesse contexto proferiu ou escreveu a frase. (Desidério Murcho)
indução
Geralmente usa-se este termo para falar de dois tipos diferentes de argumentos: as generalizações e as previsões. Uma generalização é um argumento quantificacional (ver quantificador) não dedutivo cujas premissas são menos gerais do que a conclusão. Este tipo de argumentos apresenta a seguinte forma lógica, ou outras formas lógicas análogas: “Alguns F são G. Logo, todos os F são G”. Por exemplo: “Alguns corvos são pretos; logo, todos os corvos são pretos”. Uma previsão é um argumento quantificacional não dedutivo cujas premissas se baseiam no passado e cuja conclusão é um caso particular. Por exemplo: “Todos os corvos observados até hoje são pretos; logo, o corvo do João é preto”. É defensável que qualquer argumento não dedutivo se baseia na indução, nomeadamente qualquer argumento de autoridade e argumento por analogia. Ver problema da indução. (Desidério Murcho)
inefável
Aquilo que não pode ser dito ou comunicado. (Célia Teixeira)
inferência
O processo de concluir uma afirmação a partir de outras afirmações. Por exemplo, com base nas afirmações “Deus existe” e “Se Deus existe, a felicidade eterna é possível”, pode-se inferir “A felicidade eterna é possível”. Um argumento é uma inferência, usada para efeitos de persuasão racional. (Desidério Murcho)
infinita, regressão
Ver regressão infinita.
infinitude
Ver finitude e infinitude.
informal, lógica
Ver lógica informal.
inimputabilidade
Conceito jurídico aplicado nos casos em que, tendo tido lugar uma acção que infringe a lei, se entende que o sujeito dessa acção não deve ser responsabilizado e, consequentemente, não deve ser penalizado por ela. As circunstâncias que determinam a inimputabilidade de alguém são, vulgarmente, duas: 1) a acção infractora não foi genuinamente livre, tendo o sujeito agido sob coerção; 2) a infracção não foi resultado de coerção, mas o sujeito não poderia ter consciência do que estava a fazer ou dos resultados do seu acto. O caso de alguém que seja obrigado por um terrorista a matar um inocente exemplifica a primeira circunstância; os crimes cometidos por doentes mentais ou por crianças imaturas exemplificam a segunda circunstância. Ver responsabilidade. (António Paulo Costa)
inspector de circunstâncias
Um inspector de circunstâncias é um método usado em lógica para testar a validade de alguns tipos de argumentos (ou raciocínios). Trata-se de uma sequência encadeada de tabelas de verdade em que se analisam todas as combinações possíveis (circunstâncias) de verdade e falsidade das premissas e da conclusão, de modo a verificar-se se existe alguma circunstância em que, sendo todas as premissas verdadeiras, a conclusão seja falsa — se existir, o argumento é inválido. Pelo contrário, se em todas as circunstâncias em que as premissas são verdadeiras a conclusão também é verdadeira, então o argumento é válido. Eis um exemplo: seja o raciocínio “Chove e está frio. Logo, está frio”, no qual existe apenas uma premissa (“Chove e está frio”). Se representarmos “chove” por “P”, “está frio” por “Q”, “e” por “∧” e “logo” por “⊨”, obtemos o seguinte inspector de circunstâncias:
| P Q | P ∧ Q | ⊨ | Q |
| V V | V | V | |
| V F | F | F | |
| F V | F | V | |
| F F | F | F |
Nas coluna mais à esquerda são apresentadas as quatro combinações possíveis dos valores de verdade de P e de Q. Na coluna mais à direita, são apresentados, por um lado, os valores de verdade da premissa (P ∧ Q), em função dos valores de verdade atribuídos a P e a Q em cada circunstância, e, por outro, os valores de verdade da conclusão (Q). Verificamos então que, em todas as circunstâncias (neste caso, apenas uma) em que a premissa é verdadeira, a conclusão é verdadeira. Portanto, o raciocínio é válido. Ver argumento, premissa, conclusão, valor de verdade, verdade e falsidade. (António Paulo Costa)
inteligível
Aquilo que é susceptível de ser compreendido. (Célia Teixeira)
intenção
Na filosofia da mente e na filosofia da linguagem, a intenção é definida como a propriedade de um estado mental ser acerca de algo. A crença e o desejo são frequentemente apontados como estados mentais intencionais: pode acreditar-se que a Terra é redonda, ou pode desejar-se lavar os dentes — no primeiro caso, temos em mente uma crença que é acerca da Terra; no segundo, um desejo acerca de lavar os dentes. Na filosofia da acção, a intenção é encarada como aquilo que distingue uma acção de um acontecimento não intencional associado a um agente: por exemplo, se ao cair bato com os lábios na face de uma pessoa, trata-se de um acontecimento acidental, e não da acção de beijar essa pessoa. Além disso, a intenção é um meio de racionalização das acções: por exemplo, se leio este dicionário com a intenção de me preparar para um teste, a intenção de me preparar para um teste justifica a acção de ler este dicionário. Ver vontade, deliberação e responsabilidade. (António Paulo Costa)
intencionalidade
A propriedade ou poder que alguns estados mentais têm de apontarem, se dirigem, representarem ou serem acerca de objectos, propriedades ou estados das coisas no mundo. Crenças, desejos, esperanças, ambições, intenções, amar e odiar são propriedades e estados mentais que exibem intencionalidade. Por exemplo, cremos que vai chover amanhã, desejamos e esperamos que não chova amanhã, formamos a intenção de, caso não chova, ir à praia com a Rita, amamos a Rita e odiamos a chuva, etc. Em todos estes casos há dois elementos: 1) uma certa atitude mental (medo, esperança, etc.) e 2) uma representação do mundo (da chuva, da Rita, etc.), a que em filosofia se chama conteúdo. Alguns filósofos defendem a tese, geralmente atribuída a Franz Brentano de que todos os fenómenos mentais, e só eles, exibem intencionalidade. Esta tese afirma que a intencionalidade é a marca do mental e insere-se num debate vigoroso sobre a natureza do mental que pelo menos outros tantos filósofos rejeitam, dado pensarem que não se consegue explicar a consciência fenomenal (ver consciência, qualia). Para estes filósofos, certos estados mentais, como ter dores de dentes, podem não ter intencionalidade. Este debate coloca a intencionalidade, juntamente com a consciência, no centro do debate sobre o que é ter uma mente. Não devemos confundir intencionalidade quer com intenção, quer com intensão. (Miguel Amen)
intensão
A intensão de um termo é o princípio ou a condição segundo a qual os objectos a que esse termo se refere são identificados. Por exemplo, a intensão do predicado “ser português” é a condição de ter nacionalidade portuguesa (e não a de ter nascido em Portugal, visto que há portugueses nascidos noutros países e pessoas nascidas em Portugal que não são portuguesas). Ver também compreensão, extensão, sentido. (Pedro Santos)
interpretação
A atribuição de significado a objectos, acontecimentos, textos ou discursos. Interpretar a frase “A neve é branca”, por exemplo, é atribuir um significado à frase. Compreender como se interpreta o que as pessoas dizem, e saber se podemos garantir que essa interpretação é correcta, tornou-se um problema filosófico a partir de Wittgenstein e Quine. Alguns filósofos, como Hans-Georg Gadamer (1900–2002), defenderam que a interpretação é o método próprio das ciências humanas, opondo-se ao método experimental das ciências da natureza. Por esse motivo, há quem defenda ser a “interpretação de textos” a tarefa central da filosofia. Contudo, trata-se de uma confusão, dado que mesmo os filósofos que defenderam a interpretação como método privilegiado nas ciências sociais não defenderam que interpretar textos é o objectivo do estudo da filosofia. E a maior parte dos filósofos defendem que o âmago do trabalho filosófico não é a interpretação, mas a discussão e avaliação racional dos problemas, teorias e argumentos da filosofia. Ver hermenêutica. (Desidério Murcho)
intuição
Por um lado, o conhecimento directo e autoevidente de um conceito, proposição ou entidade, por outro, a capacidade que permite obter este tipo de conhecimentos que não podem ser obtidos ou inferidos (ver inferência) por intermédio da experiência ou da razão. O conhecimento, por exemplo, de conceitos da ética, como o de bem, da estética, como o de belo, de verdades necessárias, como os princípios (ver princípio) da lógica e da matemática, ou de entidades, como Deus, é por vezes explicado assim. É habitual chamar-se “intuicionistas" às teorias que defendem o conhecimento de tais conceitos apenas através da intuição. Noutra acepção mais fraca, fala-se das intuições como as crenças que, tudo o resto sendo igual, não temos razões independentes para pensar que estão erradas. (Álvaro Nunes)
intuicionismo estético
Tipo especial de objectivismo estético que defende que as propriedades estéticas existem nos próprios objectos, embora não possam ser aprendidas pelos sentidos nem pela razão, exigindo antes uma faculdade especial a que se dá o nome de “intuição". A intuição é uma forma de conhecimento directo e é nela que encontramos, segundo o intuicionista, justificação para os nossos juízos estéticos. (Aires Almeida)
ironia
Estratégia utilizada por Sócrates, tal como é retratado nos diálogos de juventude de Platão, como parte do seu método de refutação (elenchus), em que finge ignorância e elogia a habilidade dos interlocutores para, desse modo, revelar a sua ignorância. Ver Platão, A República, (trad. 2001, Gulbenkian), 336e-337a. (Álvaro Nunes)
irracionalismo
Posição que rejeita quaisquer métodos racionais de prova. Pode defender-se o irracionalismo em várias áreas. Mas uma posição irracionalista extrema é filosoficamente insustentável. Se rejeitamos inteiramente os métodos racionais de prova, então não é possível uma defesa racional do irracionalismo. Mas se não é possível uma defesa racional do irracionalismo, então não temos quaisquer razões para o aceitar. Por outras palavras, não é possível defender uma posição irracionalista extrema pois isso implica a rejeição do próprio irracionalismo.
Em geral, as posições irracionalistas não rejeitam por completo a razão, rejeitam-na apenas em relação a uma área específica. Um exemplo é o fideísmo. Segundo esta posição, as questões religiosas são primariamente questões de fé. Neste caso, os irracionalistas podem, sem contradição, defender que a fé é superior à razão em questões religiosas. O problema muitas vezes apontado é que no interior da área em que a discussão racional é excluída, tudo vale, pois é tão legítimo acreditar, por exemplo, na existência de Deus como na do Pai Natal, o que torna as nossas posições arbitrárias. (Célia Teixeira)
J
juízo
Na lógica aristotélica, tal como foi sistematizada pelos filósofos medievais, chamava-se juízo ao acto de estabelecer uma relação entre um sujeito e um predicado, que costuma simbolizar-se como “S é P”; por exemplo: “Sócrates é mortal”. (Desidério Murcho)
juízo de facto e juízo de valor
Um juízo de facto, como “Beethoven compôs nove sinfonias” ou “A pena de morte foi abolida em Portugal”, é apenas uma tentativa de descrever as coisas. Um juízo de valor, como “As sinfonias de Beethoven são belas” ou “A pena de morte é injusta”, envolve já uma apreciação positiva ou negativa das coisas. Os juízos de facto têm valor de verdade, mas há quem pense que não se pode dizer o mesmo relativamente aos juízos de valor (ver emotivismo). Grande parte da metaética é uma tentativa de compreender o significado dos juízos de valor com conteúdo moral. Ver juízo estético, normativo e descritivo. (Pedro Galvão)
juízo de valor
Ver juízo de facto e juízo de valor.
juízo estético
Às afirmações que fazemos acerca do que é belo ou feio, acerca do que gostamos ou não e acerca dos objectos de arte chamamos “juízos estéticos”. Exemplos de juízos estéticos são “este pôr-do-sol é belo”, ou “gosto da paisagem alentejana”, ou ainda “aquela peça de dança tem ritmo e elegância”. Deve, contudo, notar-se que nem todos os juízos acerca da arte são estéticos. Por exemplo, o juízo “A Quinta Sinfonia de Beethoven tem quatro andamentos”, não é um juízo estético. Kant procurou caracterizar os juízos estéticos, distinguindo-os dos juízos de conhecimento, defendendo que os estéticos não têm qualquer carácter prático e que são subjectivos, ao contrário dos juízos de conhecimento. Por isso, os juízos estéticos são, para Kant, juízos de gosto. Ponto de vista que muitos dos filósofos posteriores rejeitam. Ver também atitude estética, experiência estética, filosofia da arte, problema do gosto e subjectivismo estético. (Aires Almeida)
justiça
Desde Aristóteles, distingue-se a justiça retributiva da justiça distributiva. Quando se discute a justificação do castigo (ver liberdade), há quem apele ao conceito de justiça retributiva dizendo que um criminoso deve sofrer um mal para pagar pelo mal que fez. O conceito de justiça distributiva tem um âmbito diferente. Clarificá-lo implica responder a este problema central na filosofia política: como devem ser distribuídos os bens sociais (riqueza, oportunidades, etc.) pelas diversas pessoas ou grupos de pessoas de uma sociedade? Algumas teorias insistem numa distribuição fortemente igualitária; outras privilegiam factores como a maximização do bem-estar (ver utilitarismo) ou o mérito pessoal. Ver igualdade, Rawls. (Pedro Galvão)
K
Kant, Immanuel (1724–1804)
Filósofo alemão. Kant nasceu em Königsberg (actual Kaliningrado), na Prússia oriental, onde estudou, trabalhou e viveu toda a sua vida, tornando-se um dos mais influentes filósofos de sempre. Durante mais de uma década trabalhou como preceptor e em 1755 juntou-se ao corpo docente da universidade de Königsberg, onde leccionou as mais variadas disciplinas: lógica, metafísica, matemática, geografia, antropologia, pedagogia, etc. É habitual dividir a sua vida intelectual em dois períodos: o “período pré-crítico” e o “período crítico”. Durante o primeiro período, Kant escreveu trabalhos menos influentes, nos quais se pode constatar a grande influência de Wolff (1679–1754), discípulo de Leibniz, e do próprio Leibniz. Kant foi também fortemente influenciado por Locke, Hume e Jean-Jacques Rousseau (1712–78). O seu período crítico teve início em 1770 com a publicação da sua Dissertação de 1770.
A Crítica da Razão Pura (1781) é a sua primeira grande obra. O problema que a domina é o de saber como é o conhecimento a priori acerca do mundo possível (ver a priori e a posteriori), ou para usar a sua terminologia, como é o conhecimento sintético a priori possível (ver analítico e sintético). Kant defendeu que não é possível saber como o mundo é em si, independentemente da nossa experiência. Sucintamente, a ideia de Kant é que o nosso aparato cognitivo, seja ele perceptivo ou puramente intelectual (ou teórico), impõe certas estruturas ao mundo. Kant defendeu que uma metafísica científica deve usar criticamente a razão na procura dos seus próprios limites: temos de procurar as “formas” que o nosso aparato cognitivo impõe ao mundo. Esta é a “revolução copernicana” de Kant: para sabermos o que podemos conhecer, temos de saber como o conhecemos.
Na Crítica da Razão Prática (1788), Kant procura os fundamentos da nossa razão prática, isto é, os fundamentos do nosso raciocínio moral. Defende que agir racionalmente é agir moralmente, é agir de acordo com o nosso dever, é agir de acordo com o imperativo categórico. Na Crítica da Faculdade do Juízo (1790), volta a defender a objectividade da razão, mas desta vez relativamente aos juízos estéticos. Contudo, esta não é meramente uma obra de estética. Nela, Kant fornece-nos uma visão global do seu sistema filosófico. (Célia Teixeira)
Kant, Immanuel, Crítica da Razão Pura (Lisboa: FCG, 1989).
Kant, Immanuel, Crítica da Razão Prática (Lisboa: Edições 70, 1997).
Kant, Immanuel, Crítica da Faculdade do Juízo (Lisboa: INCM, 1992).
Kant, Immanuel, Fundamentação da Metafísica dos Costumes (Lisboa: Edições 70, 1991).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 16 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 8 (Lisboa: Presença, 1989).
kátharsis
Termo grego que significa catarse.
Kierkegaard, Søren (1813–1855)
Pensador dinamarquês cuja obra tem um só objectivo: esclarecer o que significa a fé cristã. A fé em Deus é uma forma de vida terrivelmente exigente porque dá muito mais importância a Deus do que às coisas humanas e terrenas. Em Temor e Tremor (1843; trad. 1990, Guimarães Editores), Abraão, exemplo do amor e submissão absolutos a Deus, é considerado o modelo do homem de fé, pois para ele Deus está sempre em primeiro lugar e nem o amor a um filho lhe pode ser superior. Sem Deus o homem está condenado ao desespero. Podemos escolher uma vida dedicada ao prazer e ao divertimento (existência estética) ou ao cumprimento do dever, das obrigações morais e sociais (existência ética), mas o cristão autêntico aposta no Desconhecido e encontra nessa entrega o sentido pleno (existência religiosa). A fé cristã é sofrimento. Reina a incerteza (não sei se Deus existe) e a incompreensão dos outros, pois colocar Deus acima de tudo implica frequentemente contrariar a moral socialmente estabelecida. Critica Hegel por este ter querido tornar acessíveis à razão os dogmas da fé cristã e as Igrejas por a transformarem num hábito tranquilo e rotineiro. Um dos principais representantes do fideísmo, defende que a fé é superior à razão. Apresenta-nos uma interpretação da sua própria obra em Ponto de Vista Explicativo da Minha Obra Como Escritor (1859; trad. 1986, Edições 70). (Luís Rodrigues)
Kuhn, Thomas (1922–96)
Filósofo americano da ciência, cujas ideias acerca da noção de progresso científico se tornaram muito populares, sobretudo após a publicação de A Estrutura das Revoluções Científicas (1962; trad. bras. Editora Perspectiva, 1995). Aí apresenta uma caracterização sociológica da ciência, na medida em que parte da análise do funcionamento concreto da comunidade científica ao longo da história. Defende a ideia de que a ciência apresenta longos períodos de acumulação de conhecimentos, a que dá o nome de “ciência normal”, sendo os cientistas essencialmente conservadores, na medida em que trabalham no interior e para a preservação do paradigma dominante. Durante esse período a pesquisa científica consiste em resolver quebra-cabeças que de forma alguma põem o paradigma em causa, procurando, pelo contrário, alargar o âmbito da sua aplicação. Esses períodos de ciência normal são intercalados por breves períodos de ciência extraordinária, em que, devido à descoberta de sérias anomalias no paradigma dominante, surgem as crises e as revoluções científicas. As revoluções científicas consistem basicamente na mudança de paradigma. A sua tese mais ousada é, contudo, a de que os paradigmas são incomensuráveis (ver incomensurabilidade), correspondendo a maneiras completamente distintas de encarar a realidade. Esta tese é polémica porque implica o relativismo e a ideia de que, em rigor, não podemos falar de progresso científico. (Aires Almeida)
L
lei da natureza
Afirmação geral acerca do modo como a natureza se comporta. Normalmente, as leis da natureza têm a forma de afirmações universais do tipo, “Todo o A é B”, como por exemplo, “Todas as moléculas de água têm a mesma massa”. (Célia Teixeira)
Leibniz, Gottfried Wilhelm (1646–1716)
Filósofo racionalista alemão. Leibniz nasceu em Leipzig e morreu em Hanover. Começou a frequentar a universidade aos treze anos, doutorando-se em direito aos vinte anos. Fez importantes contribuições para a filosofia, a lógica, a geologia, a linguística, a historiografia, a matemática, a teologia, a economia, a política, a física, etc. Descobriu o cálculo infinitesimal independentemente de Newton (1642–1727). Fundou a Academia de Berlim.
Leibniz é o autor de um dos três grandes sistemas racionalistas do séc. XVII. Leibniz distingue as verdades da razão, as quais são necessárias, e as verdades de facto, as quais são contingentes (ver analítico e sintético). No domínio das verdades da razão encontram-se as verdades da matemática e da lógica, no domínio das verdades de facto encontram-se as verdades físicas e históricas. Formulou ainda o princípio da não-contradição, segundo o qual é falso tudo aquilo que leva a uma contradição e o princípio da razão suficiente, do qual dependem as verdades de facto, que nos diz que nenhuma proposição pode ser verdadeira sem que haja uma razão suficiente para que seja assim e não de outra forma. Defendeu a existência de ideias inatas. Em metafísica, defendeu a existência de mónadas, entidades espirituais individuais (os existentes actuais) e entidades ideais. Em teologia é autor de uma teodiceia, isto é, de uma solução para o problema do mal, segundo a qual este é o melhor dos mundos possíveis. Formulou o famoso princípio de identidade, conhecido como lei de Leibniz: se dois objectos são idênticos, então partilham exactamente as mesmas propriedades; e o “princípio da identidade dos indiscerníveis”: se dois objectos têm exactamente as mesmas propriedades, então são idênticos. (Célia Teixeira)
Leibniz, G. W., Discurso de Metafísica (Lisboa: Colibri, 1995).
Leibniz, G. W., Novos Ensaios sobre o Entendimento Humano (Lisboa: Colibri, 1993).
Leibniz, G. W., Princípios de Filosofia ou Monadologia (Lisboa: INCM, 1987).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 13 (Lisboa: Temas e Debates, 1999).
liberalismo
Uma das filosofias políticas mais influentes e, após a queda dos regimes da Europa de Leste que se inspiravam nas ideias de Marx, a filosofia política dominante no mundo ocidental. O liberalismo surgiu no séc. XVI como resposta ao aparecimento dos estados-nação modernos e caracteriza-se pela importância que atribui aos direitos, às liberdades (de pensamento, de expressão, de associação, de escolha, de religião e, mais recentemente, de preferência sexual) e à autonomia do indivíduo. Por este motivo, muitos liberais pensam que o papel do estado é em larga medida o de assegurar e proteger estes direitos e liberdades. No entanto, nos Estados Unidos, em reacção a posições extremas como, por exemplo, o libertarianismo de Robert Nozik (1938-2002), o liberalismo tem-se recentemente identificado com a defesa de um Estado-providência que actue em áreas como a educação, a saúde e a segurança social. Em Portugal, o liberalismo filosófico é frequentemente identificado com o “liberalismo económico” ou “neo-liberalismo” que, ao contrário daquele, é uma doutrina que dá grande importância ao mercado e a uma economia de laissez-faire. Contudo, esta identificação é fruto de uma confusão e é até frequente, como no caso de John Stuart Mill ou de Bertrand Russell, a existência de liberais que são também socialistas. O liberalismo tem sido ultimamente contestado por pensadores como o americano Michael Walzer (n. 1935), o canadiano Charles Taylor (n. 1931) e o escocês Alasdair MacIntyre (n. 1929), normalmente apelidados de “comunitarianos”, e que criticam o alegado facto de o liberalismo se apoiar numa concepção inadequada de pessoa e de negligenciar ou mesmo minar o papel da família, das tradições e da comunidade. Alguns dos principais filósofos liberais, além dos já referidos, são John Locke, Adam Smith (1723–1790), Immanuel Kant e, mais recentemente, Isaiah Berlin (1909–1997), John Rawls e Ronald Dworkin (n. 1931). (Álvaro Nunes)
Rawls, John, O Liberalismo Político (Lisboa: Presença, 1997).
liberdade
Noção central na filosofia política, que pode ser entendida em dois sentidos. A liberdade negativa consiste na ausência de coerção. Neste sentido, um indivíduo é livre desde que ninguém o force a agir ou o proíba de agir de certa maneira. A liberdade positiva consiste num controlo efectivo da própria vida. Um alcoólico, por exemplo, tem liberdade negativa caso ninguém o obrigue a beber, mas ainda assim não tem liberdade positiva. Isaiah Berlin (1909–1997), que introduziu esta distinção no artigo “Dois Conceitos de Liberdade”, defendeu que o conceito positivo de liberdade é politicamente perigoso, pois autoriza interferências indevidas do estado na vida dos indivíduos. Um problema fundamental da filosofia política, aliás, é determinar em que medida é aceitável o estado limitar a liberdade (negativa) dos cidadãos. E um dos aspectos importantes deste problema é o da justificação do castigo: por que pode o estado castigar os cidadãos privando-os da sua liberdade? Não se deve confundir estas questões políticas com o problema metafísico do livre-arbítrio. (Pedro Galvão)
libertismo
Teoria que defende uma concepção da acção incompatível quer com o determinismo, quer com o indeterminismo. Os libertistas defendem que o ser humano é um ser essencialmente livre, considerando o dilema de Hume um falso dilema. A responsabilidade do agente decorre do facto de as suas acções nem serem determinadas por causas remotas e incontroláveis (como defendem os deterministas), nem serem aleatórias (como defendem os indeterministas). O libertismo, por vezes chamado “libertarianismo”, é uma teoria metafísica que não deve ser confundida com o liberalismo económico e político, nem com o libertinismo moral. Ver causa e efeito, relação causal e compatibilismo. (António Paulo Costa)
livre-arbítrio
A capacidade para fazer escolhas. Por exemplo, eu posso aparentemente escolher ficar em casa ou ir ao café; mas não posso escolher ter ou não uma dor de cabeça. O problema filosófico do livre-arbítrio consiste em saber se as escolhas aparentes são compatíveis com o determinismo. O determinismo radical, o determinismo moderado, o indeterminismo e o libertismo constituem as respostas clássicas a este problema, sendo classificadas ora como teorias compatibilistas, ora como teorias incompatibilistas. Ver acção, compatibilismo e incompatibilismo, dilema de Hume, responsabilidade e vontade. (António Paulo Costa)
Locke, John (1632–1704)
Filósofo empirista inglês. Defendeu, contra Descartes, a inexistência de ideias inatas. Segundo Locke, a mente é como uma tábua rasa, possuindo poderes de raciocínio, mas não quaisquer conteúdos inatos. Contudo, é defensável que Locke não era realmente empirista, pois admite a existência de dois tipos de experiência (a externa e a interna), e igualmente de três tipos de conhecimento: intuitivo, que é directo e com o grau máximo de certeza; demonstrativo, que é indirecto e dá origem ao conhecimento lógico e matemático; e sensível, que diz respeito ao conhecimento da existência de objectos exteriores. Baseando-se na diferença entre qualidades primárias e secundárias das coisas, distinguiu o mundo tal como é em si do mundo tal como é para nós. Para Locke, a abstracção era uma componente central do conhecimento, que permitia a formação de ideias abstractas a partir de impressões sensíveis concretas. A distinção entre essência nominal e real é também central na sua teoria do conhecimento: assim, a essência real da água, por exemplo, é a sua constituição intrínseca, ao passo que a sua essência nominal são apenas as qualidades que atribuímos à água, mas que não correspondem à sua natureza intrínseca. É no Ensaio sobre o Entendimento Humano (1690) que Locke expõe estas ideias, entre outras.
Em ética, Locke defendeu uma versão da teoria dos mandamentos divinos; em filosofia política, defendeu o valor da tolerância política e religiosa, e a separação da igreja e do estado. As suas doutrinas da legitimação da propriedade privada, da justificação da autoridade do estado e da legitimidade da revolta contra o estado injusto são ainda hoje muitíssimo discutidas, e são apresentadas no Segundo Tratado sobre o Governo (1689). As suas ideias sobre a tolerância são apresentadas em Carta sobre a Tolerância (1689). (Desidério Murcho)
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 12 (Lisboa: Temas e Debates, 1999).
Locke, John, Ensaio sobre o Entendimento Humano, 2 vols. (Lisboa: Gulbenkian, 1999).
Locke, John, Carta sobre a Tolerância (Lisboa: Edições 70, 1997).
Locke, John, Ensaio sobre a Verdadeira Origem, Extensão e Fim do Governo Civil (Lisboa: Edições 70, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 6 (Lisboa, Presença, 1989).
lógica
O estudo da argumentação válida (ver validade e invalidade). A lógica formal estuda a argumentação cuja validade depende exclusivamente da forma lógica. A lógica informal estuda a argumentação cuja validade não depende unicamente da forma lógica. A lógica foi fundada por Aristóteles, que pela primeira vez usou a noção de forma lógica para distinguir os argumentos válidos dos inválidos (ver lógica aristotélica). A lógica conheceu relativamente poucos desenvolvimentos até Gottlob Frege e Bertrand Russell terem revolucionado a disciplina. Hoje em dia há muitos sistemas diferentes de lógica, que procuram resolver os problemas em aberto na disciplina. A chamada “lógica clássica”, de Frege e Russell, é encarada como a “lógica canónica”, e é essa que geralmente se começa por estudar.
Repare-se no seguinte argumento: 1) “Platão e Aristóteles eram filósofos; logo, Platão era um filósofo”. A lógica clássica (mas não a aristotélica) permite explicar por que razão este argumento é válido. Dado que a validade deste argumento depende inteiramente da sua forma lógica, qualquer argumento que tenha a mesma forma lógica será igualmente válido. Podemos ilustrar a forma lógica do argumento assim: “P e Q; logo, P" — sendo “P” e “Q” símbolos que representam proposições. Assim, se “P” for a proposição expressa pela frase “O aborto é um mal” e “Q” a proposição expressa pela frase “Os animais têm direitos”, obtemos o seguinte argumento válido: 2) “O aborto é um mal e os animais têm direitos; logo, o aborto é um mal”. A lógica permite também compreender por que razão são inválidos os argumentos inválidos; e permite compreender que alguns argumentos que parecem válidos são de facto inválidos (as falácias). Repare-se no seguinte argumento: 3) “Tem de haver uma só causa para todas as coisas porque todas as coisas têm uma causa”. Este argumento parece válido, mas é inválido. A lógica explica por que razão o argumento é inválido. Repare-se que o argumento seguinte é obviamente inválido: 4) “Tem de haver uma mãe para todas as pessoas porque todas as pessoas têm uma mãe”. O argumento 4 tem a mesma forma lógica do argumento 3. Mas porque o argumento 3 é mais abstracto, parece válido, apesar de o não ser. Dado que os argumentos filosóficos são geralmente muito abstractos, a lógica tem um papel crucial na filosofia: ajuda-nos a evitar erros no pensamento filosófico.
A lógica clássica tem duas partes distintas: a lógica proposicional e a lógica de predicados (também chamada “lógica quantificada”). Na lógica proposicional (ver cálculo proposicional) estudam-se argumentos cuja validade depende exclusivamente de certos aspectos da forma lógica proposicional (argumentos como 1 e 2). Os aspectos da forma lógica proposicional que contam na lógica proposicional clássica decorrem inteiramente do uso de cinco tipos de operadores: a negação, a conjunção, a disjunção, a condicional e a bicondicional (ver operador verofuncional). Assim, os argumentos 1 e 2 são válidos porque ambos dependem exclusivamente do operador de conjunção (“e”).
Na lógica quantificada ou de predicados (ver cálculo de predicados) estudam-se os argumentos que dependem exclusivamente da quantificação (ver quantificador), como é o caso dos argumentos 3 e 4. A quantificação ocorre quando se afirma ou nega que uma certa propriedade ou relação é exemplificada um certo número de vezes. Por exemplo, afirmar que há filósofos é dizer que a propriedade de ser filósofo é exemplificada por algumas coisas (nomeadamente, pessoas); afirmar que não há lobisomens é dizer que a propriedade de ser um lobisomem não é exemplificada por coisa alguma. Há muitos tipos de quantificação, mas na lógica clássica estuda-se apenas dois desses tipos: a universal e a existencial (ver quantificador universal e quantificador existencial).
Há dois aspectos fundamentais em qualquer lógica: a sua linguagem e a lógica propriamente dita. A linguagem lógica é uma forma de traduzir certos aspectos relevantes da linguagem de todos os dias numa linguagem mais transparente. O objectivo é destacar e explicitar com rigor os aspectos que se quer estudar por serem relevantes para o tipo de argumento que se tem em vista. Assim, um argumento como “Se a vida não faz sentido, Deus não existe; dado que a vida não faz mesmo sentido, Deus não existe” pode ser formalizado do seguinte modo: ¬P → ¬Q, ¬P ⊨ Q. A formalização, com os seus símbolos estranhos (ver Apêndice: Símbolos lógicos), é um instrumento crucial para se compreender com rigor a estrutura lógica do pensamento, o que por sua vez é crucial para determinar a sua validade, o que por sua vez é crucial para determinar a verdade das nossas conclusões.
Na lógica propriamente dita desenvolvem-se métodos para testar a validade das formas lógicas que se exprimem por meio da linguagem lógica (que por sua vez traduz a linguagem quotidiana). Entre esses métodos contam-se os inspectores de circunstâncias e as derivações (ver derivação). (Desidério Murcho)
Murcho, Desidério, O Lugar da Lógica na Filosofia, Capítulos 4 e 5 (Lisboa: Plátano, 2003).
Newton-Smith, W. H., Lógica: Um curso introdutório, Capítulos 1, 2, 3 e 5 (Lisboa: Gradiva, 1998).
Priest, Graham, Lógica (Lisboa: Temas e Debates, 2002).
lógica aristotélica
A lógica introduzida por Aristóteles (384-322 a.C.), e que foi posteriormente sistematizada, na idade média. Foi a única lógica conhecida no ocidente até ao advento da lógica clássica, já no séc. XIX. Trata-se de uma lógica que trabalha unicamente com quatro formas lógicas: 1) universais afirmativas (“Todo o A é B”; exemplo: “Todo o homem é mortal”); 2) universais negativas (“Nenhum A é B”; exemplo: “Nenhum deus é mortal”); 3) particulares afirmativas (“Alguns A são B”; exemplo: Alguns homens são baixos”); e 4) particulares negativas (“Alguns A não são B”; exemplo: “Alguns homens não são baixos”). A lógica aristotélica compreende duas partes: a teoria da conversão, que estuda argumentos com uma única premissa (como “Alguns homens são franceses; logo, alguns franceses são homens”), e a teoria do silogismo, que estuda argumentos com duas premissas (como “Todas as aves têm penas; todos os pardais são aves; logo, todos os pardais têm penas”). Aristóteles explicitou as relações lógicas entre as quatro formas lógicas do seu sistema, distinguindo a relação de consequência lógica (subalternidade ou implicação), a relação de contradição e a de contraditoriedade (ver quadrado de oposição). Apesar de constituir um genial monumento intelectual, a lógica aristotélica é muito restrita, carece de um fragmento proposicional (ver cálculo proposicional), aplica-se unicamente a classes que não sejam vazias, a sua aplicação à linguagem e pensamento correntes é limitadíssima e não estabelece regras de inferência válida (as chamadas “regras do silogismo” não são realmente regras de inferência, mas proibições ad hoc.). O seu interesse é hoje em dia meramente histórico. (Desidério Murcho)
Murcho, Desidério, O Lugar da Lógica na Filosofia, cap. 6 (Lisboa: Plátano, 2003).
lógica clássica
A lógica fundada por Gottlob Frege, e também por Bertrand Russell e Alfred North Whitehead (1861–1947), que abrange a lógica proposicional e de predicados. Caracteriza-se por aceitar o princípio do terceiro excluído, o princípio da não-contradição e a bivalência, operadores verofuncionais de formação de frases e a exclusão de nomes sem denotação. Foi o primeiro desenvolvimento revolucionário da lógica depois de 2400 anos de quase estagnação. Ver operador verofuncional, lógica, lógica formal. (Desidério Murcho)
lógica formal
O estudo da argumentação válida que depende exclusivamente da forma lógica. Por exemplo, a validade do seguinte argumento depende inteiramente da sua forma lógica: “Alguns homens são mortais; logo, alguns mortais são homens”. A forma lógica deste argumento é a seguinte: Alguns A são B; logo, alguns B são A. Não é difícil ver que qualquer argumento que tenha esta forma lógica é válido. Não se deve pensar que só a lógica clássica é formal; a lógica aristotélica é igualmente formal, apesar de em geral se usar menos símbolos. Os argumentos cuja validade não depende inteiramente da sua forma lógica são o objecto de estudo da lógica informal. Ver lógica. (Desidério Murcho)
lógica informal
O estudo da argumentação válida que não depende exclusivamente da forma lógica. Por exemplo, os seguintes argumentos são válidos mas não dependem exclusivamente da sua forma lógica: “Sócrates era casado; logo, não era solteiro”; “Todos os corvos observados até hoje são pretos; a cor dos corvos está geneticamente determinada; só poderia alterar-se em condições ambientais diferentes das geralmente escolhidas pelos corvos para viver; logo, todos os corvos são negros”. Os tipos mais estudados de argumentos informais são as induções (generalizações e previsões), argumentos de autoridade, argumentos por analogia e argumentos causais. Os estóicos introduziram o estudo dos aspectos pragmáticos da argumentação, anteriormente estudados na retórica, e que visam tornar os argumentos sólidos racionalmente persuasivos. Ver lógica, argumento de autoridade, indução. (Desidério Murcho)
logicismo
Projecto iniciado por Russell e Frege, que procurava mostrar que as verdades da matemática não eram senão verdades lógicas disfarçadas. Tratava-se, pois, de reduzir a matemática à lógica, no mesmo sentido em que é possível reduzir a química à física. Frege e Russell mostraram cabalmente que é possível usar a lógica de predicados para exprimir verdades simples da aritmética. Contudo, este trabalho enfrentou duas dificuldades. Em primeiro lugar, foi necessário usar a teoria de conjuntos, que não é estritamente falando uma teoria lógica; mais tarde, em segundo lugar, Gödel demonstrou em 1931 que em certos sistemas de lógica suficientemente poderosos para exprimir a aritmética nunca se poderia exprimir todas as verdades aritméticas. (Desidério Murcho)
logos
Termo grego que significa, entre outras coisas, “razão”, “argumento”, “discurso”. O termo foi introduzido na filosofia por Heraclito (cerca de 535-475 a. C.), para referir a ordem racional subjacente a toda a mudança. Opõe-se muitas vezes o logos, o pensamento racional, ao mythos, o discurso dos mitos tradicionais. Os filósofos gregos distinguiram-se por terem introduzido a ideia de que tudo é susceptível de discussão racional, incluindo as tradições religiosas e os mitos tradicionais a elas associados. (Desidério Murcho)
M
maiêutica
Nome pelo qual a personagem Sócrates, no Teeteto de Platão, designa o seu método de perguntas e respostas. O interesse da expressão está no facto de pôr ênfase no lado positivo do processo, uma vez que se trata de partejar as almas dos interlocutores de modo a que estes dêem à luz as ideias que de forma não consciente já contêm em si e que pode, por isso, ser entendido como um processo complementar da reminiscência. Nesse sentido, talvez seja mais uma noção platónica do que socrática. (Álvaro Nunes)
mal moral
O mal que resulta das más acções humanas. Por exemplo, assassínios, guerras, etc. (Célia Teixeira)
mal natural
O mal que resulta da natureza. Por exemplo, cheias, terramotos, doenças, etc. (Célia Teixeira)
mal, problema do
Ver problema do mal.
mandamentos divinos, teoria dos
Ver teoria dos mandamentos divinos.
Maquiavel, Niccolò (1469–1527)
Filósofo italiano de enorme importância na história do pensamento político. Foi considerado imoralista, adepto da ideia de que os fins justificam sempre os meios. É falso. Maquiavel não rejeita pura e simplesmente a moral, não diz que bem e mal são conceitos sem qualquer sentido. Separa a moral da política. O bom homem de estado é o que alcança e mantém o poder e não tem para tal de ser moralmente bom ou virtuoso. Seguir a moral pode ser uma desgraça para o interesse público. Em nome deste pode permitir-se, quando necessário, infracções à moral (mentiras, astúcias, crimes). A política não pode subordinar-se à moral. Se o governante quiser ser virtuoso, que o seja na sua vida privada. O realismo político de Maquiavel nega radicalmente a visão medieval e cristã da política e a perspectiva platónica, o que se pode confirmar pela leitura de O Príncipe (1532; trad. Europa-América, 1994), a sua obra mais conhecida. (Luís Rodrigues)
Marx, Karl (1818–1883)
Filósofo alemão que apresenta uma interpretação materialista da história, cujo objectivo é transformar a sociedade mediante uma actividade revolucionária consciente das condições objectivas em que se exerce. A economia é a chave da compreensão dos acontecimentos históricos. Mais do que negar a importância das ideias, Marx nega que, só por si, elas possam mudar a vida dos seres humanos. As ideias dominantes são sempre as da classe economicamente dominante. Mas nenhuma classe domina para sempre e nem sempre haverá luta de classes. A exploração e a alienação terminarão com o advento da sociedade comunista, uma sociedade sem classes. No Manifesto do Partido Comunista (1848; trad. 1999, Editorial Avante) e em A Ideologia Alemã (1846; trad. 1980, Presença), Marx pretende ter apresentado uma visão dialéctica, científica e não utópica da história: cada forma de organização social desenvolve dentro de si própria as condições da sua inevitável negação. (Luís Rodrigues)
matéria
Aquilo, seja o que for, que tem existência física e ocupa espaço; que tem forma, tamanho e se pode mover. Muitos filósofos sintetizam, dizendo que os objectos materiais são substâncias que têm extensão (ver substância), mas os cientistas têm levantado muitas dúvidas acerca da noção tradicional de matéria. Algumas formas de idealismo negam a existência de objectos materiais e algumas formas de materialismo defendem que só há objectos materiais. (Aires Almeida)
materialismo
Teoria segundo a qual toda a realidade é de natureza material ou redutível (ver reducionismo) a processos de natureza material e que, em geral, nega a existência de estados mentais independentes desses processos. A doutrina foi advogada pela primeira vez por Leucipo e Demócrito, filósofos gregos do séc. V a. C., que viram naquilo a que chamaram átomos, juntamente com o espaço, os constituintes de tudo o que existe. Os filósofos actuais, no entanto, preferem falar de fisicismo em vez de materialismo, uma vez que a física moderna concebe a matéria como sendo composta de protões, neutrões e electrões. O materialismo é ainda importante como uma possível solução para o problema da mente-corpo. Ver epicurismo, dualismo e monismo. (Álvaro Nunes)
materialismo histórico
O materialismo histórico corresponde à concepção que Marx tem da evolução histórica: 1. Uma interpretação da História que afirma que não são as ideias em si, mas sim as relações económicas de produção, que constituem os agentes fundamentais da vida social, política e espiritual do Homem; 2. Uma teoria (científica, segundo Marx) sobre a formação e o desenvolvimento das sociedades humanas, que considera que a economia é a chave da compreensão dos fenómenos históricos; 3. Uma visão da História como processo dialéctico, dinamizado por uma série de con-tradições (ver contradição) que se dão essencialmente na estrutura económica das diversas sociedades. Ver também materialismo dialéctico. (Luís Rodrigues)
máxima
Na ética deontológica de Kant, as máximas são os princípios que indicam o que leva as pessoas a agir. Pode-se fazer a mesma coisa segundo máximas diferentes, e para Kant o valor moral de um acto depende primariamente, não daquilo que se faz, mas da máxima que está subjacente àquilo que se faz. Um comerciante que não engana os clientes pode agir segundo a máxima “Devemos ser honestos”, sendo motivado pela honestidade, mas também pode agir segundo a máxima “Não enganes os outros se não queres perder clientes”, sendo neste caso motivado pelo interesse pessoal. Kant afirma que só no primeiro caso o acto do comerciante tem valor moral. Ver também dever, imperativo categórico, vontade boa. (Pedro Galvão)
mecanicismo
Concepção da natureza, típica de filósofos e cientistas modernos, como Galileu, Descartes e Newton, segundo a qual tudo o que acontece se pode explicar à luz de forças físicas que provocam “puxões” e “empurrões”. Tal como qualquer máquina, a natureza é composta por inúmeras “peças” ligadas entre si, cujo funcionamento regular e previsível pode ser reduzido a um conjunto limitado de leis, as leis da mecânica. Por isso o mecanicismo é uma forma de reducionismo. O mecanicismo surgiu como oposição às concepções organicista e animista da natureza, herdadas de Aristóteles e dos teóricos medievais. As descobertas do físico escocês James Maxwell (1831–79) acerca da radiação electromagnética abalaram seriamente a concepção mecanicista da natureza. (Aires Almeida)
mediação
Ver imediatez e mediação.
metaética
Área da ética que, em vez de se ocupar de teorias normativas (ver normativo e descritivo) relativas àquilo que devemos fazer ou ao tipo de pessoa que devemos ser, investiga a própria natureza dessas teorias e da moralidade em geral. Na metaética discute-se, por exemplo, até que ponto e em que sentido a ética depende da razão ou da emoção. Outro problema importante é o de saber por que motivo havemos de agir moralmente. Uma questão central nesta área é a de saber se e como os juízos morais são objectivos (ver objectivo e subjectivo). Entre as teorias que procuram esclarecer esta questão, contam-se o realismo moral, o subjectivismo moral, o emotivismo, o relativismo moral e a teoria dos mandamentos divinos. Ver Hare. (Pedro Galvão)
metafilosofia
Chama-se “metafilosofia" às teorias acerca da natureza da filosofia. Estas teorias não tratam conceitos como, por exemplo, os de verdade, bem, justiça, dever, beleza, ser, conhecimento, etc.; nem respondem a problemas como, por exemplo, o de saber se todas as desigualdades são injustas ou se existe um sentido da vida, etc.. Em metafilosofia examina-se a natureza dos problemas filosóficos, como se devem estudar as teorias e os argumentos da filosofia, ou que papel desempenha a interpretação de textos, o conhecimento do contexto histórico ou o domínio da lógica no trabalho filosófico. Por exemplo, quando se discute a utilidade, a historicidade ou a universalidade da filosofia está-se em pleno campo metafilosófico. (António Paulo Costa)
metafísica
O estudo dos aspectos conceptuais mais gerais da estrutura da realidade. Por exemplo: Serão todas as verdades relativas, ou haverá verdades absolutas? E o que é a verdade? Ao longo do tempo um ser humano muda de personalidade, fica fisicamente diferente, perde cabelo, etc. — como se pode então dizer que é a mesma pessoa? Será que a vida faz sentido? Será que temos livre-arbítrio? A ontologia é a disciplina da metafísica que estuda quais as categorias de coisas que há. Por exemplo: Será que há números, ou são meras construções humanas? Terão os universais, como a brancura, existência independente dos particulares, isto é, das coisas brancas? Serão as possibilidades não realizadas reais, ou meras fantasias? O que hoje em dia se chama “lógica filosófica” abrange em grande parte os temas da metafísica tradicional, introduzidos na obra Metafísica, de Aristóteles, designadamente o problema da identidade e persistência de objectos ao longo do tempo. A designação de “metafísica”, contudo, não foi introduzida por Aristóteles, que usava a expressão “filosofia primeira”, muito corrente ainda no séc. XVII, mas hoje pouco usada — o que é uma pena, pois não permite o trocadilho informativo que consiste em dizer que a filosofia primeira estuda as questões últimas. No sentido popular do termo, “metafísica” quer dizer algo totalmente diferente: o “estudo” de questões que transcendem a realidade material: ocultismo, espiritismo, etc. Em filosofia, a metafísica não é nada disto.
A metafísica é uma das disciplinas centrais e mais gerais da filosofia; muitas outras disciplinas abordam problemas metafísicos particulares. Por exemplo: a filosofia da acção estuda, entre outras coisas, o problema metafísico de saber o que é e como se individua uma acção (isto é, como se distinguem as acções umas das outras); a filosofia da ciência estuda, entre outras coisas, o problema ontológico de saber se as entidades inobserváveis postuladas pelas ciências (como os quarks) têm existência real e independente de nós, ou se são meras construções humanas.
Com o desenvolvimento da ciência moderna, a partir do séc. XVII, a metafísica começou a sofrer ataques por não produzir resultados à semelhança da ciência; afinal, era a ciência empírica, como a física, que produzia conhecimento seguro sobre a natureza última das coisas, e não a metafísica. Esses ataques começam com Kant. Posteriormente, algumas escolas de filosofia, como o positivismo lógico, encaravam a metafísica como coisa mítica do passado. Contudo, na filosofia contemporânea, a força dos problemas metafísicos voltou a impor-se, e o seu estudo floresceu uma vez mais. (Desidério Murcho)
Russell, Bertrand, Os Problemas da Filosofia, Caps. 9 e 10 (Coimbra: Almedina, 2001).
Nagel, Thomas, Que Quer Dizer Tudo Isto?, Caps. 9 e 10 (Lisboa: Gradiva, 1995).
metáfora
Um recurso literário em que se usa uma ideia ou imagem para falar de outra coisa que não essa ideia ou imagem. A alegoria da caverna de Platão, por exemplo, é usada não para falar de cavernas e escravos, mas para falar de alguns aspectos importantes do conhecimento e da atitude das pessoas relativamente a ele. Assim, o interesse de uma metáfora não é a ideia ou imagem usada, mas o que esse uso significa. (Desidério Murcho)
método científico
Conjunto de procedimentos usados pelos cientistas para obter um conhecimento tão certo (ver certeza) e seguro quanto possível na sua área de investigação. Até aos primeiros anos do séc. XX, uma concepção de método baseada na indução e derivada das ideias de Francis Bacon (1561–1626) e de Galileu Galilei teve a preferência dos cientistas. A descoberta de que algumas teorias científicas, consideradas verdadeiras com base nesse método eram, na realidade, falsas, levou à formulação de metodologias alternativas, das quais a mais importante e conhecida é o falsificacionismo de Karl Popper. Outras tentativas de explicar a investigação científica, como a de Thomas Kuhn, que, em vez de formular teorias normativas e racionalistas (ver racionalismo) da ciência, procura descrever (ver normativo e descritivo) a forma como progride, ou como a de Paul Feyerabend, ao defender a inexistência do método científico e a ideia de que “qualquer coisa serve”, têm sido por muitos consideradas irracionalistas (ver irracionalismo). Ver experiência, explicação científica, falsibicabilidade, filosofia da ciência, generalização, incomensurabilidade, método experimental, método hipotético-dedutivo, problema da indução, verificabilidade, verificacionismo. (Álvaro Nunes)
método experimental
O método experimental é o conjunto de procedimentos científicos que incorporam sistematicamente a experimentação como forma de estabelecer a verdade e falsidade de uma certa hipótese científica. A padronização dos testes experimentais possibilita a sua repetição em quaisquer situações análogas e permite uma confirmação independente dos resultados pela comunidade científica, o que não acontece com os enunciados não científicos e pseudocientíficos. Dada a importância da exactidão dos dados a utilizar, o método experimental exige um aparato técnico progressivamente mais sofisticado, com o qual se ampliam as limitadas capacidades naturais de percepção humana. Embora exista uma concepção largamente difundida do método experimental segundo a qual este consiste na sequência observação — hipótese — experimentação — lei ou reformulação da hipótese, em filosofia da ciência discute-se a correcção desta descrição. Ver Galileu, falsificabilidade, corroboração, método científico e método hipotético-dedutivo. (António Paulo Costa)
método hipotético-dedutivo
Trata-se de um método empregue na ciência para avaliar uma certa hipótese acerca dos fenómenos em estudo. Neste método, formula-se uma dada hipótese sob a forma de uma premissa com a forma lógica de uma afirmação condicional, que se submete a um teste que a confronta com os factos, deduzindo-se então se é, ou não, uma hipótese correcta (ver dedução). Imagine-se que um cientista, ao descobrir uma dada substância, formula a seguinte hipótese: “Se esta substância é água, então entra em ebulição a 100º centígrados”. Em seguida, o cientista vai testar esta hipótese submetendo a substância à temperatura de 100º centígrados. Se a substância não entrar em ebulição àquela temperatura, o cientista deduz que não é água e que a hipótese era falsa (ver verdade e falsidade). O seu raciocínio tem a forma lógica de um modus tollens e pode ser formalizado da seguinte maneira:
Premissa da hipótese: Se esta substância é água, então entra em ebulição a 100º centígrados.
Premissa do teste: Esta substância não entra em ebulição a 100º centígrados.
Conclusão: Logo, esta substância não é água.
Pelo contrário, se a substância entrar em ebulição àquela temperatura, a hipótese é corroborada (ver corroboração). Em filosofia da ciência é habitual contrastar o método hipotético-dedutivo com o método indutivo (ver indução e Mill), em que as leis são generalizações feitas com base na experiência de um número significativo de fenómenos particulares. Ver falsificabilidade, generalização, explicação científica, método científico e método experimental. (António Paulo Costa)
milagres
Intervenções divinas que violam uma lei da natureza. Exemplos de milagres são fenómenos como a levitação de santos, a transformação de água em vinho, etc. Os milagres são por vezes usados como premissas de argumentos a favor da existência de Deus: se os milagres são o resultado da intervenção divina, então revelam a existência de Deus. Hume objectou à existência de milagres, defendendo que é sempre mais provável que os relatos de milagres sejam falsos do que tenham de facto acontecido as coisas extraordinárias que relatam. Ver filosofia da religião. (Célia Teixeira)
Mill, John Stuart (1806–1873)
Filósofo inglês, tornou-se o principal representante do empirismo no séc. XIX. Mill defendeu que todo o conhecimento científico — até o matemático — resulta de inferências indutivas realizadas a partir da experiência sensível (ver indução), propôs um conjunto de métodos para avaliar tais inferências e introduziu a concepção nomológico-dedutiva das explicações científicas (ver explicação científica). Na ética, Mill destacou-se como defensor do utilitarismo, tendo associado esta teoria a uma versão peculiar de hedonismo, segundo a qual, mais do que a quantidade, interessa a qualidade dos prazeres de que desfrutamos. Contra o hedonismo do seu predecessor, Jeremy Bentham (1748–1832), sustentou que os prazeres mentais são intrinsecamente superiores aos corporais, de tal modo que os primeiros são preferíveis seja qual for a duração e intensidade dos segundos. Na filosofia política, Mill advogou o liberalismo. Argumentou decisivamente a favor da liberdade de pensamento e expressão, bem como da igualdade entre homens e mulheres. Algumas das suas obras mais importantes são Utilitarismo (1861; trad. 1976, Atlântida Editora), Sobre a Liberdade (1859; trad. 1997, Europa-América). (Pedro Galvão)
mimêsis
Termo grego para “imitação”. Segundo Platão e Aristóteles, trata-se de uma noção central da estética. A ideia é que as artes imitam o mundo real. A noção foi submetida a fortes críticas, a mais notória das quais foi a de Nelson Goodman. (Desidério Murcho)
modus ponens
O nome da seguinte forma válida da lógica proposicional: “Se P, então Q; P; logo, Q”. Por exemplo: “Se a vida é sagrada, o aborto é um mal; a vida é sagrada; logo, o aborto é um mal”. Trata-se de uma das formas lógicas mais usadas na argumentação corrente; é tão usada, que muitas vezes se omite a segunda premissa e a própria conclusão, afirmando-se apenas a primeira premissa. (Desidério Murcho)
modus tollens
O nome da seguinte forma válida da lógica proposicional: “Se P, então Q; não Q; logo, não P”. Por exemplo: “Se Deus existe, o mal não existe; mas o mal existe; logo, Deus não existe”. Trata-se de uma das formas lógicas mais usadas na argumentação corrente; é tão usada, que muitas vezes se omite a segunda premissa e a própria conclusão, afirmando-se apenas a primeira premissa. (Desidério Murcho)
mónada
Termo popularizado por Gottfried Wilhelm Leibniz na obra Princípios de Filosofia Ou Monadologia (trad. 1987, INCM) para designar as substâncias básicas individuais (ver substância) que constituem o universo. As mónadas são entidades únicas, indestrutíveis, imateriais, sem extensão nem partes, semelhantes a almas, e dotadas de percepção (representação das coisas) e de apetição (tendência para ter sucessivas percepções). As mónadas diferem pelo grau de percepção de que são capazes e, embora não tenham quaisquer relações entre si, estão perfeitamente sincronizadas umas com as outras por intermédio de uma harmonia pré-estabelecida. Os objectos do mundo material são colecções de mónadas. (Álvaro Nunes)
moral
O mesmo que ética. Contudo, usa-se por vezes o termo “moral” não como sinónimo de ética mas para referir os costumes de um povo, independentemente de serem relevantes ou não para a ética, costumes esses enraizados em determinadas tradições, muitas vezes de carácter religioso. Assim, uma pessoa pode considerar que é imoral trabalhar ao Sábado, não no sentido filosófico de ser eticamente condenável, mas apenas no sentido de ser proibido pela sua tradição religiosa. Do ponto de vista ético, trabalhar ou não trabalhar ao Sábado poderão ser escolhas igualmente legítimas. É neste sentido que se distingue um moralista de um eticista. Um moralista é alguém que defende ou condena certos costumes com base em tradições religiosas ou culturais; um eticista é um especialista em ética, que defende ou condena certas práticas com base numa argumentação filosófica. (Desidério Murcho)
mundo exterior
O mundo que percepcionamos através dos sentidos, do qual também fazemos parte e no qual agimos no nosso dia-a-dia. Diz-se “exterior” para o distinguir de conteúdos mentais, como pensamentos, ideias, desejos, crenças, etc., de que temos experiência directa e que, portanto, constituem o nosso mundo interior ou mental. Saber se temos ou não acesso directo ao mundo exterior, ou até se existe algo a que possamos chamar mundo exterior, é alvo de disputa entre os partidários do realismo e do idealismo. (Aires Almeida)
mundo sensível
O mundo da maneira como é percepcionado pelos nossos sentidos. Platão considerava que esse era um mundo de falsas imagens e ilusões, contrapondo-o ao “mundo inteligível”, apenas acessível à razão e onde podemos encontrar a verdade. Ver também alegoria da caverna. (Aires Almeida)
mutatis mutandis
Expressão latina que significa “fazendo as mudanças necessárias”. Por exemplo, pode-se dizer que as críticas de Sócrates à sociedade superficial e acrítica do seu tempo se podem fazer à sociedade de hoje, mutatis mutandis. (Desidério Murcho)
N
nada
A inexistência de todas as coisas. Na filosofia de Sartre, é a indeterminação da acção humana, que está na origem da liberdade de escolha (ver libertismo, livre-arbítrio). Na filosofia de Heidegger, é a ausência das coisas ou a frustração das nossas expectativas relativas à sua presença. Um dos problemas mais interessantes que a palavra levanta é saber se exprime um nome ou um quantificador. Assim, na frase “Nada me preocupa”, se “nada” exprime um nome, então parece estar sugerido que algo me preocupa (o nada); se, porém, exprime um quantificador, a frase significa que não há coisa alguma que me preocupe. (Artur Polónio)
não-contradição, princípio da
Chama-se “princípio da não-contradição" à ideia de que duas afirmações contraditórias não podem ser ambas verdadeiras nem ambas falsas. Por exemplo: dado que as afirmações “Sócrates é alto” e “Sócrates não é alto” são contraditórias, o princípio declara que não podem ser ambas verdadeiras nem ambas falsas. Quando uma lógica aceita o princípio da não-contradição significa que qualquer afirmação com a forma “P e não P” será uma falsidade lógica. Algumas lógicas modernas recusam este princípio, como é o caso da lógica paraconsistente. Não se deve confundir a não-contradição com o princípio da bivalência: este último é a ideia de que só há dois valores de verdade e que todas as proposições têm um dos dois, e só um dos dois. Não se deve também pensar que a não-contradição é de alguma maneira um axioma da lógica clássica; na verdade, é um resultado, um ponto de chegada, e não um ponto de partida. Aristóteles defende o princípio na sua obra Metafísica (Γ 4). Note-se que a redução ao absurdo só é válida caso se aceite o princípio da não-contradição. (Desidério Murcho)
necessário e contingente
Diz-se que uma verdade é necessária se não podia ter sido falsa. Ou seja, sejam quais forem as circunstâncias, é verdadeira. Por exemplo, sejam quais forem as circunstâncias, dois mais dois são quatro. Diz-se que uma verdade é contingente quando é verdadeira mas poderia ter sido falsa. Por exemplo, é verdadeiro que Aristóteles foi um filósofo, mas isto poderia ter sido falso. Se Aristóteles, por exemplo, se tivesse dedicado exclusivamente à agricultura, não teria sido um filósofo. Há filósofos que rejeitam esta distinção. Não se deve confundir o necessário e contingente com o analítico e sintético, nem com o a priori e a posteriori. (Célia Teixeira)
negação (¬)
Uma proposição da forma “não P”, que é verdadeira se P for falsa e vice-versa. Por exemplo: “A vida não tem sentido” é a negação de “A vida tem sentido”. A negação é por vezes enganadora. Intuitivamente, a negação de “Todas as verdades são relativas” é “Nenhuma verdade é relativa”; mas isto é falso. A negação correcta é “Algumas verdades não são relativas”. (Desidério Murcho)
negação da antecedente, falácia
Ver falácia da negação da antecedente.
neopositivismo
Ver positivismo lógico.
Nietzsche, Friedrich (1844–1900)
O pensamento deste filósofo alemão é uma radical crítica à cultura ocidental, segundo Nietzsche envenenada por uma atitude antinatural que desvaloriza o mundo sensível (o mundo do devir), tudo o que é corpóreo e sobrevaloriza a razão. Sócrates e Platão são os criadores desta perspectiva, mas é a moral cristã que sofre as mais violentas críticas porque a desenvolveu e popularizou, como procura mostrar em Para a Genealogia da Moral (1887). A moral cristã transformou em dever o desprezo pelo que é terreno. O fundamento da mensagem religiosa e moral que, em nome de um paraíso artificial, transforma a vida num inferno é Deus. Um tal Deus é incrível. A “morte de Deus” significa que a fé em Deus morreu, como anuncia em O Anticristo (1888). Nietzsche pensa que a “morte de Deus” é uma “Boa Nova” porque permitirá libertar a vida de uma negação doentia. Sobre a vida humana já não pesa o fardo do Além nem a ameaça do Juízo Final. Contudo, se encaminhar a vida para Deus era um grandioso desperdício, será um mesquinho desperdício não criar novos valores. O não a Deus deve ser acompanhado pelo sim à vida, o não ao céu pelo sim à terra. Para vencer o niilismo que desde Sócrates intoxicou a cultura ocidental devemos colocar esta vida acima de qualquer negação, preferi-la a todo e qualquer outro valor. É por isso que, ao contrário do que às vezes se diz, Nietzsche não é niilista. Opõe-se aos valores criados pela moral cristã e pela cultura ocidental, na medida em que, eles sim, reduzem a nada (nihil) o valor deste mundo. Encobriu-se esse niilismo com expressões como “reino de Deus”, “vida eterna” e “o outro mundo”, com a finalidade de negar o mundo terreno, passando a ideia de que, em si, nada é. A “sagração da vida”, do mundo do devir, um “sim sem reservas” e para sempre ao único mundo real, eis o que definirá o novo modelo de Homem, tão exigente e difícil de conseguir como o sim à vida em todos os seus aspectos. Por isso, Nietzsche dar-lhe-á o nome de Super-homem.
Há também quem considere Nietzsche imoralista, como parece patente no próprio título de Para Além do Bem e do Mal (1886). Mas isso só é correcto se por tal se entender que pretende destruir a moral cristã, a moral do não à vida. O seu objectivo é libertar a vida da moral cristã substituindo-a por uma moral que celebre a vida na sua totalidade, mesmo nos seus aspectos chocantes e dolorosos. Nietzsche recusou-se escrever no estilo dos filósofos tradicionais, exprimindo-se através de afirmações contundentes e aforísticas. A sua escrita é bastante metafórica e com um recorte literário evidente, como se verifica em Assim Falava Zaratustra (1883-91), a sua obra mais aclamada. (Luís Rodrigues)
Kenny, Anthony, História Concisa da Filosofia Ocidental, capítulo19, (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 11 (Lisboa: Presença, 1989).
Nietzsche, Friedrich, Assim Falava Zaratustra (Lisboa: Relógio d'Água, 2000).
Nietzsche, Friedrich, O Anticristo; Ecce Homo; Nietzsche Contra Wagner (Lisboa: Relógio d'Água, 2000).
Nietzsche, Friedrich, Para a Genealogia da Moral (Lisboa: Relógio d'Água, 2000).
Nietzsche, Friedrich, Para Além do Bem e do Mal (Lisboa: Relógio d'Água, 1999).
Reale, Giovanni e Antiseri, Dário, História da Filosofia, volume 3 (São Paulo: Edições Paulinas,1990).
Vattimo, Gianni, Introdução a Nietzsche (Lisboa: Presença, 1990).
niilismo (do latim “nihil", que significa “nada”)
Designa a convicção de que a existência e a vida não têm sentido ou finalidade. O niilista nega que haja princípios morais aceitáveis. Associa-se o termo a uma concepção radicalmente pessimista que considera a vida um erro e propõe a negação da vontade de viver. A noção de niilismo desempenha um papel importante na filosofia de Nietzsche. O problema central do seu pensamento é como ultrapassar o niilismo. Considera-o uma interpretação da existência que negou os valores autênticos e a vontade de viver esta vida por si mesma. Tal interpretação começou, segundo Nietzsche, com Platão e Sócrates e foi popularizada e reforçada pelo Cristianismo. A célebre declaração “Deus morreu” é a consequência lógica do desenvolvimento da metafísica e da moral ocidentais que tornaram Deus indigno de crença. A morte de Deus torna claro para quem a sabe interpretar que os valores tradicionais nada valiam e exige a criação de valores que consagrem o que em seu nome se negou: esta vida e este mundo. (Luís Rodrigues)
noesis
Termo grego usado por Platão para referir o mais elevado tipo de conhecimento. (Desidério Murcho)
non sequitur
Expressão latina que significa literalmente “não se segue”. Diz-se dos argumentos (falaciosos) em que a conclusão não se segue das premissas. Ver falácia. (Aires Almeida)
normativo e descritivo
Uma oposição quando à maneira como se faz a correspondência entre as afirmações e a realidade (o que os filósofos chamam “o sentido da correspondência”). Numa afirmação normativa pretende-se fazer corresponder a realidade à afirmação; numa afirmação descritiva pretende-se fazer corresponder a afirmação à realidade. Por exemplo: “Não devemos maltratar os animais” é uma afirmação normativa, pois pretende que aconteça na realidade o que se afirma; e “A Terra é redonda” é uma afirmação descritiva, pois pretende que a afirmação represente a realidade. Alguns filósofos defendem, contudo, que esta distinção é superficial e enganadora. Por exemplo, diz-se por vezes que a ética e a lógica são disciplinas normativas; mas é perfeitamente possível defender que são disciplinas que procuram descrever o que o bem e a validade realmente são e não o que as pessoas pensam que são — e, neste caso, são disciplinas descritivas como a história ou a física. Ver juízo de facto e juízo de valor. (Desidério Murcho)
nous
Termo grego para “mente”. O termo foi usado por Platão e outros filósofos anteriores a Aristóteles, mas foi este último que lhe deu um significado mais sistemático, muito semelhante ao que hoje entendemos por “espírito”, “mente” ou a res cogitans de Descartes: a parte cognitiva do ser humano. (Desidério Murcho)
númeno
Conceito utilizado por Kant para designar qualquer realidade que não possa ser objecto da nossa experiência (intuição sensível). Como o conhecimento humano não se estende além da experiência, o númeno é inacessível (por exemplo, Deus). Opõe-se ao fenómeno porque este está ao alcance da intuição sensível e do conhecimento científico. Como os limites do nosso conhecimento não têm de ser os limites da realidade, podemos pensar que, apesar de incognoscível, o númeno existe. O númeno é o que pode ser pensado como existente em si. O fenómeno existe como algo que pode ser conhecido. (Luís Rodrigues)
O
objectivismo estético
Doutrina acerca da justificação dos juízos estéticos, de acordo com a qual juízos como “x é belo” dependem da existência de certas características em x. Há, assim, características objectivas em virtude das quais as coisas belas são belas. Esta doutrina opõe-se ao subjectivismo estético, dado que, na opinião do objectivista, o belo não é subjectivo nem depende dos gostos das pessoas. O que conta não são os sentimentos que temos quando apreciamos os objectos, mas o que faz parte integrante dos próprios objectos. O filósofo americano Monroe Beardsley (1915-85) é um dos representantes contemporâneos do objectivismo estético. (Aires Almeida)
objectivismo e subjectivismo
Distinção fundamental acerca da natureza das afirmações da metafísica, mas também da epistemologia, da ética e da estética. O objectivismo defende que as verdades de alguma ou algumas áreas do conhecimento são independentes do nosso conhecimento ou experiência delas. Assim, por exemplo, o objectivismo em ética é a ideia de que o valor de verdade dos juízos éticos, como “Não se deve torturar pessoas inocentes”, é independente do que possamos pensar desse juízo, ou das perspectivas de cada sujeito. Em oposição a isso, os subjectivistas defendem que o valor de verdade dos juízos éticos, estéticos, metafísicos ou epistemológicos depende fortemente da perspectiva que cada sujeito tem da “realidade”. O subjectivismo estético, por exemplo, defende que não se pode dizer que a Nona Sinfonia de Beethoven é bela ou não: a beleza está nos olhos do observador. Note-se que é possível defender o subjectivismo ético, por exemplo, e ao mesmo tempo rejeitar o subjectivismo metafísico, sem qualquer contradição. (Aires Almeida)
objectivo e subjectivo
Distinção entre o que é independente do sujeito e o que depende apenas do sujeito (sentimentos, pensamentos, crenças, desejos, etc.). Ver objectivismo e subjectivismo e qulidades primárias e secundárias. (Aires Almeida)
obra de arte
Saber quais são os objectos que podem ser classificados como obras de arte é um dos principais problemas da filosofia da arte: o problema da definição de arte. Alguns filósofos pensam que há propriedades essenciais (ver definição essencialista) às obras de arte, que permitem classificá-las como tal, divergindo entre si quanto à identificação de tais propriedades. Outros pensam que existem propriedades necessárias e suficientes (ver condição necessária e suficiente), mas não essenciais, sendo antes de carácter contextual e institucional. Outros ainda, afirmam não ser possível identificar um conjunto de propriedades fixas, comuns a todas as obras de arte. Deve salientar-se que não são apenas objectos físicos, como quadros e esculturas, que contam como obras de arte. Uma canção, uma interpretação teatral ou o conjunto de movimentos que constituem uma peça de dança também podem ser obras de arte. Ver também definição explícita e parecença familiar. (Aires Almeida)
observação
Quando é espontânea consiste em pouco mais do que ter experiências (ver experiência) ou sensações casuais e tem pouco interesse científico. A observação sistemática, pelo contrário, permite produzir e testar teorias e, por isso, é de grande importância para as ciências empíricas. A observação científica realiza-se em condições controladas, procura responder a questões previamente estabelecidas e exige a recolha, o exame e o registo sistemáticos e objectivos (ver objectivo e subjectivo) dos dados observados. O termo é também frequentemente usado para designar uma das fases do método experimental. Ver experiência científica, verificabilidade. (Álvaro Nunes)
Ockham, William of (1285–1347)
Também conhecido por Guilherme de Ockham. Filósofo e teólogo franciscano inglês, Ockham fez contribuições importantes para diversas áreas da filosofia como a lógica, a metafísica, a teoria do conhecimento, a ética e a filosofia política. É, no entanto, conhecido sobretudo pela sua defesa do nominalismo, o ponto de vista segundo o qual os universais (ver universal) não são coisas reais, mas apenas nomes ou conceitos (ver conceito); e pelo princípio metodológico conhecido como “navalha de Ockham” ou princípio da parcimónia (“as entidades não devem ser multiplicadas para além do necessário”), que recomenda a simplicidade como critério na construção de teorias (ver teoria). A polémica em que se envolveu com o Papa João XXII sobre a “pobreza apostólica" conduziu, em 1328, à sua excomunhão e fuga para Pisa e depois para Munique, cidade onde, sob a protecção de Luís da Baviera, passou o resto dos seus dias e onde escreveu sobretudo defendendo a separação entre a Igreja e o Estado. (Álvaro Nunes)
ontologia
Disciplina da metafísica que estuda quais as categorias de coisas que há. Por exemplo: Será que há números, ou são meras construções humanas? Terão os universais, como a brancura, existência independente dos particulares, isto é, das coisas brancas? Serão as possibilidades não realizadas reais, ou meras fantasias? Por que razão há coisas e não nada? Por vezes, usa-se erradamente o termo “ontologia” para falar de metafísica, isto é, para falar do estudo da natureza última das coisas. (Desidério Murcho)
operador verofuncional
Um operador verofuncional é uma conectiva proposicional (por exemplo, a conjunção “e” ou o advérbio “não”) que se combina com uma ou mais frases para originar outra, mais complexa. Por exemplo, as frases “Cavaco Silva quer ser Presidente” e “Santana Lopes quer ser Presidente” podem combinar-se por meio da conectiva “e” para formar a frase complexa “Cavaco Silva quer ser Presidente e Santana Lopes quer ser Presidente”. Quando temos um operador verofuncional, o valor de verdade da frase mais complexa é determinado apenas pelos valores de verdade das frases que a compõem; diz-se então que esse valor de verdade é uma função dos valores de verdade das frases componentes — daí a designação “verofuncional”. Defende-se usualmente que conectivas como “e” e “ou” são verofuncionais (do mesmo modo que as suas traduções “∧” e “∨” do cálculo proposicional). Com efeito, é razoável defender que frases da forma [A e B] são verdadeiras se quer A quer B forem verdadeiras e são falsas se pelo menos uma delas for falsa; e frases da forma [A ou B] são falsas se quer A quer B forem falsas, e verdadeiras se pelo menos uma delas for verdadeira. Pelo contrário, operadores como o de crença (“acredita que”) não são verofuncionais: o valor de verdade da frase “o João acredita que Paulo Portas é culpado” não depende, de nenhum modo, do da frase “Paulo Portas é culpado”. O modo como cada operador verofuncional determina o valor de verdade das frases em que ocorre é representado numa tabela de verdade. (Pedro Santos)
opinião
A expressão de uma crença. Uma distinção fundamental em epistemologia, introduzida por Platão, é a distinção entre crença (ou opinião) e conhecimento. Podemos achar que vamos almoçar fora, e acabarmos por não ir. Mas se soubermos que vamos almoçar fora (se isso for verdadeiramente conhecimento), então vamos mesmo almoçar fora. Isto significa que o conhecimento, mas não a crença, é factivo; isto é, podemos acreditar em coisas falsas, mas não podemos saber coisas falsas. Por outras palavras, podemos acreditar em falsidades, mas não podemos saber falsidades. (Célia Teixeira)
oposição, quadrado de
Ver quadrado de oposição.
organon
Termo grego para “instrumento”. Aristóteles usou o termo para designar um conjunto de obras que tratam de lógica, formal e informal, que ele considerava um instrumento da filosofia e do conhecimento em geral. (Desidério Murcho)
ousia
Termo grego para “substância” ou, literalmente, “ser”. Aristóteles usava o termo para referir a primeira das suas categorias. O ser ou a substância de uma coisa é o que subjaz a todas as mudanças que uma coisa sofre ao longo do tempo. (Desidério Murcho)
P
padrão de gosto
Diz-se daquilo que tem agradado, de um modo geral, às pessoas de diferentes épocas e lugares e que serve de critério para justificar os nossos juízos de gosto. Para Hume o padrão de gosto é algo que pode ser empiricamente observado. Como subjectivista, Hume defende que os juízos estéticos são juízos de gosto. Mas defende também que daí não se segue que os gostos são todos iguais. Os gostos discutem-se na medida em que existe um critério geral de justificação: o padrão de gosto. O padrão de gosto surge da nossa disposição para reagir com agrado ou desagrado a certas características dos objectos. É por isso que, para qualquer pessoa informada e com um gosto refinado, isto é, conhecedora do padrão de gosto, se torna disparatado afirmar que a música do Quim Barreiros é melhor do que a de Beethoven. Ver também subjectivismo estético e teoria do gosto. (Aires Almeida)
panteísmo
A concepção de Deus, segundo a qual todas as coisas que existem são partes ou manifestações de uma única realidade divina. Assim, Deus e o mundo são uma e a mesma coisa, pelo que Deus é imanente e não transcendente. A ideia de um Deus criador e providencial é afastada pelo panteísta, pelo que este se afasta, simultaneamente, das concepções monoteístas e politeístas; distingue-se também do teísmo, do deísmo e do ateísmo, embora alguns filósofos teístas o considerem uma forma disfarçada de ateísmo. O panteísmo costuma ser associado aos estóicos (ver estoicismo), mas os seus mais destacados defensores foram Espinosa (1632–77) e Hegel. (Aires Almeida)
paradigma
1. Um modelo de algo.
2. Em filosofia da ciência é uma noção introduzida por Thomas Kuhn e que desempenha um papel central na maneira como esse filósofo caracteriza a actividade científica. O termo nem sempre é usado por Kuhn da mesma maneira. Mas há dois sentidos principais e complementares: por um lado refere a teia de crenças, valores, processos, técnicas e instrumentos partilhados pelos membros da mesma comunidade científica; por outro, designa um tipo de resultado particular que se torna exemplar e, por isso, se constitui como modelo na base do qual os cientistas acabam por trabalhar. A “Astronomia Ptolomaica” e a “Astronomia Copernicana” constituem diferentes paradigmas, assim como a “Óptica Corpuscular” e a “Óptica Ondulatória”. (Aires Almeida)
paradoxo
1. Estamos perante um paradoxo quando um argumento aparentemente sólido conduz a uma afirmação aparentemente falsa ou contraditória. Porque a afirmação é falsa ou contraditória, somos levados a recusá-la; mas, por outro lado, não é fácil ver como se pode fazê-lo, dado que há um argumento aparentemente sólido a seu favor. Por exemplo, a afirmação “Esta afirmação é falsa” é paradoxal porque se for verdadeira, é falsa, e se for falsa, é verdadeira. Mas isto colide com a ideia de que não pode haver frases declarativas com valor assertivo que não sejam verdadeiras nem falsas. Nem sempre é fácil ver que argumento é colocado em causa por um paradoxo. Resolve-se um paradoxo mostrando que o argumento em que se baseia não é sólido: porque é inválido ou porque depende de premissas falsas. Muitas vezes, a descoberta das premissas falsas envolvidas num paradoxo está na origem de descobertas fundamentais na área teórica em causa. Mais raramente, resolve-se um paradoxo afirmando que a conclusão que parecia falsa ou contraditória não o é. Não se deve confundir paradoxo com falácia.
2. Em termos populares, chama-se paradoxo apenas a qualquer afirmação contraditória. (Desidério Murcho)
parcimónia, princípio da
Também conhecido como navalha de Ockham, em referência ao filósofo nominalista medieval Guilherme de Ockham (c. 1285–1349), este princípio afirma que não devemos postular a existência de entidades sem necessidade. É comum usar este princípio para decidir entre duas teorias concorrentes. Por exemplo, se uma teoria explicar o movimento dos átomos através de forças de atracção e repulsão e outra apelar a essas mesmas forças mais um diabo responsável pela deslocação desses átomos, então a primeira teoria é melhor. (Célia Teixeira)
parecença familiar
Certas coisas exemplificam um mesmo conceito, porque partilham certas características, apesar de estas poderem ser diferentes de caso para caso. São tais semelhanças que permitem estabelecer uma relação de familiaridade entre coisas que podem até ser muito diferentes entre si. Tal como um filho pode ter os olhos parecidos com os da mãe, o nariz com o do avô e a boca com a do bisavô, mas não haver qualquer característica comum a todos. Esta ideia deve-se a Wittgenstein, que deu o exemplo do conceito de jogo, e é utilizada na filosofia da arte pelo filósofo Morris Weitz (1916-87). Segundo Weitz, o conceito de arte não pode ser definido, embora possamos reconhecer como arte obras completamente inovadoras, o que acontece devido a haver parecenças familiares entre estas e alguma das obras anteriores. (Aires Almeida)
particular
Em metafísica, um particular é aquilo que é único e irrepetível, como Jorge Sampaio, Coimbra e a minha bicicleta. Os particulares distinguem-se dos universais, como a brancura, a circularidade e a sabedoria, que são propriedades exemplificadas por particulares numericamente distintos, isto é, por várias coisas. (Aires Almeida)
Pascal, aposta de
Ver aposta de Pascal.
pensamento caprichoso
Falácia com a seguinte forma: “Era bom que fosse verdade que P; logo, P”. Por exemplo: era bom que me saísse a lotaria; logo, vai-me sair a lotaria. Se em contextos práticos a falácia é imediatamente visível, em contextos filosóficos é menos evidente: “Se Deus não existisse, a vida não faria sentido; mas seria horrível que a vida não fizesse sentido; logo, Deus existe”. (Desidério Murcho)
per accidens
Expressão latina: “por acidente”. Usa-se sobretudo na lógica aristotélica para referir os seguintes padrões de inferência, a que se chamam “conversão per accidens”: “Todo o A é B; logo, algum B é A”; e “Nenhum A é B; logo, algum B não é A”. As duas inferências só são válidas pressupondo que há objectos da classe A. (Desidério Murcho)
per se
Expressão latina que significa “por si mesmo”. Alguns teólogos afirmam que Deus existe per se. (Aires Almeida)
percepção
A percepção é o modo como tomamos consciência dos objectos, em especial daquilo que nos é dado pelos sentidos. A pergunta que muitos filósofos colocam acerca da percepção é a seguinte: será que o facto de percepcionarmos objectos é suficiente para justificar a existência desses objectos fora da nossa consciência? A distinção entre aparência e realidade parece indicar que há diferença entre aquilo que as coisas são e a maneira como tomamos consciência delas, isto é, a maneira como as percepcionamos. O modo como funciona a percepção dá lugar a grandes disputas filosóficas e é um tema central nas discussões acerca da natureza do conhecimento. Há três grandes teorias da percepção, com diferentes implicações em termos epistemológicos: o realismo directo, o realismo representativo e o idealismo. Ver também realismo crítico e realismo ingénuo. (Aires Almeida)
pergunta complexa, falácia da
Ver falácia da pergunta complexa.
petição de princípio
Ver falácia da circularidade.
petitio principii
Expressão latina: petição de princípio. Ver falácia da circularidade.
phronêsis
Termo grego que refere a prudência, isto é, o conhecimento prático e moral. Aristóteles usou o termo para referir o tipo de raciocínio recto em matérias éticas que é de esperar de uma pessoa virtuosa. (Desidério Murcho)
physis
Termo grego que significa “natureza física” e também “ordem natural”. Na Antiguidade Grega opunha-se a physis ao nomos (leis ou costumes humanos) e debatia-se se as leis humanas (nomeadamente éticas e políticas) estavam inscritas na natureza das coisas, ou se eram meras convenções. Ver relativismo e ética. (Desidério Murcho)
Platão (427-347 a. C.)
Filósofo grego que, juntamente com Sócrates, seu mestre, e Aristóteles, seu discípulo, é uma das figuras mais importantes da filosofia ocidental. Nasceu em Atenas, numa família aristocrática, e, como era comum na época e nos jovens da sua classe, ter-se-ia dedicado à política activa não o tivesse dela afastado, primeiro, o governo dos Trinta Tiranos e, depois, a execução de Sócrates, em 399. Apesar disso, fez várias viagens à Sicília com o objectivo de influenciar Dionísio II, tirano de Siracusa, e a sua filosofia está profundamente marcada por preocupações de carácter ético (ver ética) e político (ver filosofia política). Fundou em Atenas, em 387, uma escola dedicada ao ensino e à investigação, chamada Academia, onde ensinou até ao final da sua vida. Com excepção da Apologia de Sócrates (trad. 1993, INCM), todas as outras obras que escreveu são diálogos, que é comum distribuir por três períodos: juventude, maturidade e velhice. As obras do primeiro período tratam de conceitos morais específicos, como a piedade (Êutifron) ou a coragem (Laques) e nelas Sócrates é a figura central; as obras de maturidade expõem as suas principais teorias (teoria das ideias, da imortalidade e transmigração das almas); e nas obras de velhice, critica e revê algumas das teorias dos diálogos de maturidade. Defendeu que aquilo que várias acções justas têm em comum é o facto de participarem da ideia ou Forma de justiça. As Ideias são eternas e imutáveis, ao passo que as coisas sensíveis, que delas participam, são perecíveis e mutáveis. Existe uma hierarquia do ser, desde as imagens, artefactos (ver artefacto) e seres vivos, que constituem o mundo sensível e que são objecto de opinião, até às entidades matemáticas e às Ideias (de que a suprema é a Ideia incondicionada de Bem), que constituem o mundo inteligível e cujo conhecimento consiste na recordação (ver reminiscência) daquilo que a alma imortal contemplou aquando da sua existência separada do corpo. A justiça consiste em cada um desempenhar na cidade a função para a qual a sua natureza é mais adequada e a sociedade justa é aquela em que os cidadãos estão distribuídos por três classes, de acordo com a sua natureza: guardiões, que têm a seu cargo o governo; guerreiros, que protegem a cidade dos inimigos; e artesãos, a que pertencem a generalidade dos habitantes. As contribuições de Platão para vários domínios da filosofia são tão importantes que houve quem afirmasse que toda a filosofia posterior é apenas uma nota de rodapé à sua obra. Ver alegoria da caverna, dialéctica, inteligível, universais. (Álvaro Nunes)
Hare, R. M., O Pensamento de Platão, (Lisboa: Presença, 1998).
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 3 (Lisboa: Temas e Debates, 1999).
Koyré, Alexandre, Introdução à Leitura de Platão, (Lisboa: Presença, 18987).
Koyré, Alexandre, Galileu e Platão (Lisboa: Gradiva, 1986).
Magee, Brian, Os Grandes Filósofos, cap. 1 (Lisboa: Presença, 1989).
Platão, Êutifron, Apologia de Sócrates, Críton (Lisboa: INCM, 1993).
Platão, Laques, (Lisboa: Edições 70, 1989).
Platão, Hípias Maior (Lisboa: Ed. 70, 2000).
Platão, Hípias Menor (Coimbra: INIC, 1990).
Platão, Cármides (Coimbra: INIC, 1988).
Platão, Lísis (Coimbra: INIC, 1990).
Platão, Íon (Lisboa: Editorial Inquérito, 1988).
Platão, Protágoras (Lisboa: Relógio D'Água, 1999).
Platão, Górgias (Lisboa: Edições 70, 1997).
Platão, Ménon, (Lisboa: Colibri, 1992).
Platão, Fédon (Coimbra: Minerva, 1998).
Platão, Crátilo, (Lisboa: Sá da Costa Ed., 1994).
Platão, Fedro, (Lisboa: Edições 70, 1997).
Platão, O Banquete, (Lisboa: Edições 70, 1991).
Platão, A República (Lisboa: Gulbenkian, 2001).
Platão, Parménides, (Lisboa: Instituto Piaget, 2001).
política, filosofia
Ver filosofia política.
Popper, Karl (1902–1994)
Filósofo da ciência britânico (nascido na Áustria) cuja obra teve um grande impacto não só entre os filósofos, mas também entre os próprios cientistas. Em Viena partilhou com os fundadores do positivismo lógico um interesse profundo pelo conhecimento científico. O avanço do nazismo levou-o a emigrar para a Nova Zelândia e, mais tarde, para Inglaterra. A filosofia da ciência de Popper, conhecida por falsificacionismo, proporciona uma solução original para estes dois problemas: 1) O que distingue as teorias científicas das não científicas? 2) O que caracteriza o método científico? Popper responde a 1 defendendo que uma teoria é científica apenas se for falsificável, isto é, se for incompatível com algumas observações possíveis. Assim, quando uma teoria genuinamente científica é falsa, em princípio podemos revelar a sua falsidade recorrendo à observação. Já as teorias pseudo-científicas, como as que encontramos na astrologia, permanecem intactas perante quaisquer observações — mas por essa razão acabam por nada dizer sobre aquilo que observamos. Quanto a 2, Popper defendeu uma certa perspectiva do método científico. Defendeu, mais precisamente, que a melhor maneira de fazer ciência é elaborar imaginativamente teorias ou conjecturas ousadas, mas submetê-las depois a testes rigorosos concebidos para as refutar ou falsificar. As melhores teorias científicas são as que resistem a tais testes. Um aspecto importante da perspectiva da filosofia da ciência de Popper é a sua rejeição da indução. Outro aspecto a salientar é a sua crítica ao relativismo de filósofos como Kuhn: contra estes filósofos, Popper sustentou que a ciência nos proporciona conhecimento objectivo e uma imagem do mundo cada vez mais próxima da verdade (ver realismo). Popper destacou-se ainda na filosofia política pela sua firme oposição a todas as formas de totalitarismo, tendo criticado a este respeito as ideias de Platão, Hegel e Marx. Ver corroboração. (Pedro Galvão)
Losee, John, Uma Introdução Histórica à Filosofia da Ciência, Capítulo XI (Lisboa: Terramar, 1998).
Popper, Karl, A Lógica da Pesquisa Científica (São Paulo: Cultrix, 1974).
Popper, Karl, A Sociedade Aberta e os seus Inimigos, 2 vols. (Lisboa: Fragmentos, 1993).
Popper, Karl, Conjecturas e Refutações (Coimbra: Almedina, 2003).
Popper, Karl, O Mito do Contexto (Lisboa: Edições 70, 1999).
positivismo
Posição filosófica introduzida pelo filósofo e sociólogo francês Auguste Comte, segundo a qual o verdadeiro conhecimento advém dos dados dos sentidos. O positivismo é assim uma forma radical de empirismo. Comte defendeu que o pensamento humano se divide em três estádios evolutivos: o religioso, o metafísico e o científico. Os primeiros são estádios primitivos de aquisição de conhecimento, os quais serão eventualmente abolidos à medida que evoluímos. O positivismo de Comte é uma teoria descritiva e normativa do conhecimento humano. Descritiva, porque pretende dar conta do modo como o nosso conhecimento de facto evolui. Normativa, porque pretende fornecer regras acerca do modo como devemos alcançar o conhecimento. Esta posição deu origem a outras versões de positivismo, entre elas o positivismo lógico. (Célia Teixeira)
positivismo lógico
Também conhecido por neopositivismo e por empirismo lógico, este movimento filosófico começou nos anos vinte do séc. passado com o Círculo de Viena e foi muito influente nas décadas seguintes. Empenhados em promover uma maneira científica de fazer filosofia, os positivistas lógicos advogaram um empirismo radical hostil à metafísica, defenderam a unidade da ciência e propuseram a verificabilidade como critério de significado. No âmbito da metaética, a adopção deste critério motivou o emotivismo. Os positivistas lógicos desenvolveram estudos incontornáveis em áreas como a filosofia da linguagem e a filosofia da ciência. Alguns dos seus membros mais influentes foram Moritz Schlick (1882–1936), que fundou o movimento, Carnap, Otto Neurath (1882–1945) e Friedrich Waismann (1896–1959). Wittgenstein foi uma presença informal no grupo, Popper o seu mais acérrimo crítico e A. J. Ayer (1910–89) o seu divulgador britânico. (Pedro Galvão)
possibilidade e impossibilidade
Uma possibilidade é algo que pode ser verdade, ainda que não seja realmente verdade. Por exemplo, Sócrates chamava-se “Sócrates”, mas poderia ter-se chamado “Diógenes”. Evidentemente, tudo o que é realmente verdade é uma possibilidade. E todas as necessidades são também possibilidades: por exemplo, se admitirmos que é necessário que 2 + 2 = 4, então é possível que 2 + 2 = 4 (ver necessidade e contingência). Uma impossibilidade é algo que não pode ser verdade, além de não ser realmente verdade. Por exemplo, não só não é verdadeiro que 2 + 2 = 5, como é impossível que 2 + 2 = 5. Evidentemente, nada do que é realmente verdade é impossível. A lógica modal estuda a argumentação que envolve os conceitos de possibilidade e necessidade. Apesar de os exemplos dados se referirem à matemática, há filósofos que defendem que nem todas as necessidades são de carácter matemático ou lógico (como “A água é H2O” ou “Sócrates era um ser humano”). (Desidério Murcho)
post hoc ergo propter hoc
Expressão latina que significa literalmente “depois disso, logo por causa disso”. Ver falácia post hoc.
post hoc, falácia
Ver falácia post hoc.
postulado
Uma proposição que se admite como verdadeira sem qualquer prova. Desejavelmente, os postulados são auto-evidentes ou pelo menos amplamente aceitáveis. (Desidério Murcho)
pragmática
A pragmática analisa os aspectos do significado que dependem do modo como a linguagem é usada e das intenções comunicativas dos falantes — distinguindo-se por isso da semântica, que se ocupa tipicamente do significado literal das expressões linguísticas. Por outras palavras, a pragmática estuda os significados implícitos que a elocução (ou a escrita) de uma frase ou sequência de frases pode ser capaz de comunicar. Por exemplo, eu posso responder a uma pergunta sobre o paradeiro do Rui dizendo “Está um carro amarelo em frente da casa da Ana”, o que permite ao meu interlocutor inferir que o Rui está em casa da Ana (e que tem um carro amarelo). As regras de funcionamento deste mecanismo de comunicação de significados implícitos são, desde que ele foi descoberto pelo filósofo H.P. Grice (1913–88), objecto privilegiado do estudo da pragmática. Mais geralmente, a disciplina estuda os princípios que regem a produção de sequências linguísticas, consideradas como acções (ou actos de fala). J.L. Austin (1911–60) e J. Searle (n. 1932) formularam teorias gerais dos actos de fala. Os tópicos de que a pragmática se ocupa foram originalmente discutidos em filosofia da linguagem, e esta disciplina tem com a pragmática o mesmo tipo de problemas de fronteira que tem com a semântica. Ver também asserção. (Pedro Santos)
pragmatismo
Corrente filosófica segundo a qual a eficácia na aplicação prática fornece o critério para determinar a verdade das proposições (ver proposição). Assim, uma proposição é verdadeira se for, na prática, vantajoso sustentá-la, ou, na versão de William James (1842–1910), se funcionar. Isto significa que o conhecimento é um instrumento para organizar a experiência e os conceitos (ver conceito) são hábitos de crença ou regras de acção. Os pragmatistas pensam que a experiência humana é um processo histórico, contingente (ver necessário e contingente) e evolutivo e consideram que muitos dos problemas filosóficos têm origem em dualismos (como teoria-prática e realidade-aparência), que derivam de teorias do conhecimento que concebem as crenças como representações (ver representação) e, por isso, chamaram a atenção para a continuidade entre experiência e natureza, e para a reciprocidade entre teoria e prática, entre conhecimento e acção e entre factos e valores (ver valor). O pragmatismo começou com a adopção por Charles S. Peirce (1839–1914), por volta de 1870, da descrição de uma crença como um hábito de acção em vez de uma representação da realidade, e entre os pragmatistas clássicos contam-se também William James e John Dewey (1859–1952). Para Peirce, o significado de uma proposição é determinado pelas suas consequências experimentais observáveis, que permitem estabelecer padrões objectivos (ver objectividade e subjectividade) de verdade. Para James, ao contrário, é a ideia de eficácia e de sucesso das pessoas individuais que fornece o padrão de apreciação de uma proposição. Dewey, por seu lado, vê a investigação como um processo cujos procedimentos e normas têm de ser avaliados e revistos à luz da experiência subsequente. Esta revisão é, no entanto, um processo social e comunitário, feito com base nos valores das pessoas vulgares. Assim, desde o início que existem duas tendências no pragmatismo, uma objectivista, associada à obra de Peirce e outra, subjectivista, mais próxima das posições de James. Actualmente, a influência do pragmatismo faz-se sentir na obra de filósofos americanos contemporâneos como W. V. Quine, Donald Davidson (1917-2003), Hilary Putnam (n. 1926) e Richard Rorty (n. 1931). (Álvaro Nunes)
James, William, O Pragmatismo (Lisboa: INCM, 1997).
prática
Termo que significa “acção” ou “actividade” e que foi introduzido por Aristóteles para, por oposição a theoria (teoria) e poiêsis (arte), referir as acções (ver acção) que têm origem numa escolha deliberada e pertencem à esfera da vida ética e da política. O termo foi usado por Marx e pelos marxistas posteriores (Gramsci, Lukács e Sartre) para afirmar a primazia da actividade humana concreta, consciente e livre, capaz de transformar a natureza, a sociedade e o homem, sobre a teoria. Na linguagem comum, a prática é frequentemente entendida em oposição a teoria. Ver alienação, teoria. (Álvaro Nunes)
prática, razão
Ver razão prática.
práxis
Ver prática.
predicado
Uma palavra (ou conjunto de palavras) que exprime uma propriedade ou uma relação. Por exemplo, o predicado “é alto” exprime a propriedade de ser alto. Os predicados podem ser relacionais ou não relacionais. Um predicado é relacional quando relaciona pelos menos dois particulares. Por exemplo, o predicado “é filho de” na frase “O João é filho de Miguel”, relaciona o João com o Miguel. (Célia Teixeira)
premissa
Uma afirmação usada num argumento para sustentar uma conclusão. Por exemplo, a premissa do argumento “O aborto não é permissível porque a vida é sagrada” é a afirmação “A vida é sagrada”. Ver entimema. (Desidério Murcho)
pré-socráticos
O termo refere-se aos filósofos que surgiram antes de Sócrates, sendo que muitos deles procuravam compreender a origem, a constituição e a natureza do mundo físico, tendo apresentado as primeiras teorias cosmológicas. Os pré-socráticos mais importantes foram Tales de Mileto, Anaximandro e Anaxímenes (da escola jónia de meados do séc. VI a. C.), Pitágoras de Samos (c. 429-347 a. C.), Heraclito de Éfeso (c. 560–475 a. C.), Empédocles de Agrigento (c. 493–c. 433 a. C.), os eleatas Parménides (n. c. 515 a. C.) e Zenão (n. c. 490 a. C.), os atomistas Demócrito (460–370 a. C.) e Leucipo (c. 450 a. C.) e ainda Anaxágoras de Clazómenas (c. 499- 427 a. C.). (Aires Almeida)
prima facie
Expressão latina que significa “à primeira vista”. Em ética, distinguem-se os deveres prima facie dos deveres absolutos. Dizer, como Kant, que temos o dever absoluto de não mentir é pensar que mentir é sempre errado. Dizer que não mentir é um dever prima facie implica reconhecer que, embora à partida seja errado mentir, mentir é a melhor opção ética em certas circunstâncias excepcionais. (Pedro Galvão)
princípio
As ideias mais gerais e elementares nas quais se procura basear qualquer investigação, conduta, sistema teórico, etc. Em filosofia os princípios abundam em todas as áreas. Há o princípio do terceiro excluído em lógica, o princípio do duplo efeito em ética, o princípio da verificação em filosofia da linguagem, o princípio da perfeição em metafísica, etc. Princípios esses que nem sempre são aceites por todos os filósofos, estando frequentemente associados a determinadas doutrinas filosóficas. (Aires Almeida)
princípio do terceiro excluído
Chama-se “princípio do terceiro excluído” à ideia de que, para qualquer afirmação P, é verdadeiro que P ou não P. Ou seja: o princípio declara que não há uma terceira possibilidade, entre P e não P, seja qual for a afirmação. Por exemplo: relativamente à afirmação “Sócrates é alto”, só há estas duas alternativas: “Sócrates é alto” ou “Sócrates não é alto”. Quando uma lógica aceita o princípio do terceiro excluído significa que qualquer afirmação com a forma “P ou não P” será uma verdade lógica. Algumas lógicas modernas recusam este princípio, como é o caso da lógica intuicionista. Não se deve confundir o terceiro excluído com o princípio da bivalência: este último é a ideia de que só há dois valores de verdade e que todas as proposições têm um dos dois, e só um dos dois. A relação precisa entre o terceiro excluído e a bivalência é objecto de disputa filosófica. Não se deve também pensar que o terceiro excluído é de alguma maneira um axioma da lógica clássica; na verdade, é um resultado, um ponto de chegada, e não um ponto de partida. (Desidério Murcho)
problema da demarcação
Ver critério de demarcação.
problema da indução
Problema de responder ao argumento de Hume cuja conclusão é que os argumentos indutivos (ver indução), por muito fortes que pareçam, não têm o menor fundamento. Hume sugere que os argumentos indutivos pressupõem um princípio da uniformidade da natureza. Por exemplo, depois de observarmos muitos pedaços de metal que dilataram ao serem aquecidos, inferimos indutivamente que todos os pedaços de metal dilatam quando são aquecidos ou que o próximo pedaço de metal que aquecermos também dilatará, mas uma inferência como esta só é razoável sob o suposto de que a natureza tem uma forte estabilidade. No entanto, que razões temos para acreditar que a natureza é uniforme? Podemos dizer o seguinte: temos observado que a natureza é uniforme; logo, a natureza em geral é uniforme e continuará a ser uniforme. O problema é que esta justificação para o princípio da uniformidade da natureza consiste ela própria num argumento indutivo e, portanto, pressupõe também a ideia de que natureza é uniforme. Assim, torna-se impossível evitar uma regressão infinita quando tentamos justificar a indução e, deste modo, parece que as inferências indutivas não têm justificação racional. Popper aceitou o cepticismo de Hume a este respeito, mas procurou preservar a racionalidade da ciência defendendo que esta só recorre à dedução. (Pedro Galvão)
problema do gosto
Há quem defenda que os juízos estéticos, como “isto é belo”, são apenas juízos de gosto, sendo portanto subjectivos. Ora, isso levanta o seguinte problema: como é possível manter o carácter subjectivo desse tipo de juízos estéticos sem cair no cepticismo? Se tais juízos são subjectivos, então as pessoas não estão a falar da mesma coisa quando afirmam “isto é belo”, pelo que não é possível discutir o assunto. Mas é contraditório dizer que a estética é a discussão daquilo que não se pode discutir, pelo que o subjectivismo estético tem de responder a esta objecção. (Aires Almeida)
problema do mal
O problema de reconciliar a existência do Deus teísta com o mal existente no mundo. A formulação clássica do problema do mal é da autoria de Epicuro (341–270 a. C.): “Quer Ele [Deus] impedir o mal, mas não pode? Então é impotente. Pode, mas não quer? Então é malévolo. Será que pode e quer? Donde vem então o mal?”. Há várias formas de responder a este problema. Uma das respostas mais populares entre os filósofos consiste em defender que se não existisse mal no mundo, os seres humanos nunca poderiam exibir aquilo que de mais valioso têm, nomeadamente, as suas qualidades morais não existiriam Madres Teresas nem heróis. Outra das respostas consiste em defender que se não existisse mal, não poderíamos ter livre-arbítrio. E é melhor um mundo com mal mas no qual temos livre-arbítrio do que um mundo sem mal mas sem livre arbítrio. (Célia Teixeira)
problema filosófico
A filosofia, tal como a ciência, procura resolver problemas que nos afectam a todos. A diferença está no tipo de problemas que a filosofia enfrenta. A filosofia trata de problemas conceptuais, para os quais não dispomos de meios empíricos de prova, acerca dos fundamentos da ciência, da religião, da arte, e até do nosso dia-a-dia. Por exemplo, problemas como o de saber o que é a justiça, o que é o conhecimento, qual o mecanismo através do qual os nomes referem as coisas que referem, etc. Muitas vezes tomam-se como filosóficos problemas que claramente o não são. Por exemplo, saber se a religião contribui para a coesão das sociedades não é um problema filosófico, mas sociológico. Ver também filosofia. (Aires Almeida)
proposição
O pensamento literalmente expresso por uma frase declarativa. Diferentes frases ou afirmações podem exprimir a mesma proposição: “Lisboa é uma cidade” e “Lisbon is a city” exprimem a mesma proposição. (Desidério Murcho)
proposição categórica
Tradicionalmente, aquelas proposições da forma sujeito-predicado prefixada por um quantificador. Aristóteles distinguiu quatro tipos de proposições categóricas:
Tipo A: Universal Afirmativa: Todo o S é P; Todos os filósofos são inteligentes.
Tipo E: Universal Negativa: Nenhum S é P; Nenhum filósofo é inteligente.
Tipo I: Particular Afirmativa; Algum S é P; Alguns filósofos são inteligentes.
Tipo O: Particular Negativa; Algum S não é P; Alguns filósofos não são inteligentes.
Contudo, as proposições de tipo A e E são, na verdade condicionais quantificadas. Ver proposição hipotética, silogismo. (Célia Teixeira)
proposição hipotética
Tradicionalmente, proposições condicionais (ver condicional), como a expressa pela frase “Se Sócrates é homem, então é mortal”. Ver proposição categórica, implicação. (Célia Teixeira)
propriedade
1. Uma qualidade ou característica que algo possui. Por exemplo, dizer que João é inteligente é dizer que João tem a propriedade de ser inteligente. As propriedades são expressas através de predicados não relacionais (ver predicado). As propriedades são os exemplos típicos de universais.
2. Noutro sentido, o termo “propriedade” refere o património de alguém, aquilo que pode ser adquirido ou dispensado por alguém. Num sentido mais amplo, “propriedade” pode servir para referir as posses não materiais de alguém, como a liberdade e a vida. (Célia Teixeira)
pura, razão
Ver razão pura.
Q
quadrado de oposição
Diagrama que ilustra as diversas relações lógicas entre as quatro formas lógicas da lógica aristotélica:
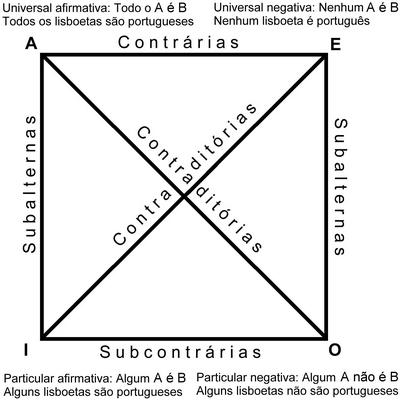
Assim, entre as formas lógicas A e I, por um lado, e E e O, por outro, há uma relação de subalternidade: A implica I, e E implica O. Esta relação é falsa, a menos que se excluam classes vazias; mas sem ela a lógica aristotélica cai por terra. De modo que é necessário excluir todas as proposições que falsificam a relação de subalternidade. Para isso, exclui-se todas as proposições que se refiram a classes vazias (classes como “lobisomens”, que não têm elementos). Com base na mesma exclusão de classes vazias é possível afirmar que as formas A e E são contrárias, isto é, que não podem ser ambas verdadeiras, mas podem ser ambas falsas. Ainda com base na mesma exclusão é possível afirmar que as formas I e O são subcontrárias, isto é, que não podem ser ambas falsas, mas podem ser ambas verdadeiras. A única relação do quadrado que não depende da exclusão de classes vazias é a de contraditoriedade ou negação, que existe entre A e O, por um lado, e entre E e I, por outro. Isto significa que A e O têm sempre valores de verdade opostos: se A for verdadeira, O será falsa e vice-versa; se E for verdadeira, I será falsa, e vice-versa. O diagrama é ainda hoje útil para ilustrar a negação correcta de proposições universais. (Desidério Murcho)
Murcho, Desidério, O Lugar da Lógica na Filosofia, cap. 6 (Lisboa: Plátano, 2003).
qualidades estéticas
As características ou propriedades que certos objectos supostamente exemplificam e que os fazem ter valor estético. Assim, um objecto que não exemplifique qualquer qualidade estética também não tem qualquer valor estético. Apenas os partidários do objectivismo estético defendem a existência de qualidades estéticas. Intensidade, complexidade, unidade, equilíbrio formal e proporção costumam ser referidas como qualidades estéticas. (Aires Almeida)
qualidades primárias e secundárias
Distinção entre qualidades ou características dos objectos. As primárias são qualidades intrínsecas dos objectos, independentes da mente ou sujeito que as percebe. Por isso são às vezes chamadas “qualidades objectivas”. As secundárias apenas são causadas pelos objectos percepcionados, na medida em que têm essa capacidade, mas que dependem da maneira como a mente do sujeito reage quando os percepciona. Por isso são às vezes chamadas “qualidades subjectivas”. Forma, tamanho e estrutura interna são qualidades primárias, enquanto a cor, o odor e o sabor são qualidades secundárias. Esta distinção é feita por Galileu, Descartes e Locke, estando subjacente à ciência moderna. Mas filósofos idealistas como Berkeley rejeitam-na. Ver também realismo. (Aires Almeida)
quantificador
Qualquer dispositivo linguístico usado para dizer quantos particulares (ou propriedades) exemplificam uma dada propriedade. Por exemplo, podemos dizer que alguns filósofos são gregos; estamos nesse caso a dizer que um número indeterminado de particulares (os filósofos) tem uma certa propriedade (são gregos). Ou podemos dizer que algumas cores são brilhantes; estamos neste caso a dizer que um número indeterminado de propriedades (as cores) tem uma certa propriedade (são brilhantes). Assim, termos como “alguns”, “todos”, “pelo menos cinco”, “mais de cem”, “a maioria”, “poucos”, “nenhuns”, “apenas um”, etc., são quantificadores. Na lógica clássica e aristotélica usam-se apenas dois quantificadores: o quantificador universal e o quantificador existencial; contudo, a lógica clássica permite definir muitos outros quantificadores com base nestes, como “exactamente três”, por exemplo (mas não quantificadores como “a maioria de”). (Desidério Murcho)
quantificador existencial
Expressões como “alguns”, “pelo menos um”, etc., são quantificadores existenciais, simbolizados habitualmente na lógica clássica com um E ao espelho: ∃. A negação de um quantificador existencial é um quantificador universal, porque negar que alguns filósofos são imortais é o mesmo do que afirmar que todos os filósofos são mortais. Ver quantificador. (Desidério Murcho)
quantificador universal
Expressões como “todos”, “nenhum”, etc., são quantificadores universais, simbolizados habitualmente na lógica clássica com um A (da palavra alemã Alle, tudo) ao contrário: ∀. A negação de um quantificador universal é um quantificador existencial, porque negar que todos os filósofos são gregos é o mesmo do que afirmar que alguns filósofos não são gregos. Ver quantificador. (Desidério Murcho)
Quine, Willard van Orman (1908-2000)
Filósofo americano e um dos filósofos contemporâneos mais influentes. Após o doutoramento, Quine viajou para a Europa, onde contactou com o lógico polaco Tarski (1901/2–1983) e com os filósofos do Círculo de Viena (ver positivismo lógico), os quais exerceram uma influência determinante na sua formação intelectual. Quine defendeu uma forma radical de empirismo na qual não há lugar para o conhecimento a priori (ver a priori e a posteriori). A sua rejeição da distinção analítico e sintético é ainda hoje extremamente influente. Esta rejeição mostrou as fraquezas do projecto positivista de salvar o conhecimento a priori reduzindo-o (ver reducionismo) ao mero conhecimento linguístico, e mostrou também as dificuldades que as noções de significado e de necessidade levantam para uma filosofia naturalista. Quine defendeu que os únicos factos cientificamente aceitáveis para estabelecer uma teoria do significado são factos acerca do comportamento linguístico dos falantes, o que o levou a concluir que o significado é indeterminado. Entre as suas obras mais importantes encontram-se From a Logical Point of View (1953), Word and Object (1960) e The Ways of Paradox and Other Essays (1966). (Célia Teixeira)
R
raciocínio
O mesmo que inferência. (Desidério Murcho)
racionalismo
1. A posição filosófica segundo a qual a razão tem um papel preponderante na aquisição de conhecimento. O racionalismo é assim o oposto do empirismo. Tal como existem versões radicais de empirismo que negam à razão qualquer papel na aquisição de conhecimento, também as versões mais radicais de racionalismo negam aos sentidos qualquer papel na aquisição de conhecimento. Contudo, ao passo que ainda hoje em dia há quem defenda posições empiristas radicais, as posições racionalistas radicais só foram populares na Grécia antiga. As versões mais moderadas de racionalismo defendem que tanto a razão como os sentidos são fontes substanciais de aquisição de conhecimento. Há que não confundir a ideia de que podemos adquirir conhecimento a priori acerca do mundo com a ideia de que o conhecimento não seria possível sem termos experiência do mundo. Uma coisa é como adquirimos os conceitos relevantes usados na formulação das nossas crenças acerca do mundo, os quais podem ser adquiridos através da experiência; outra coisa é saber se, na posse dos conceitos relevantes, podemos ou não saber coisas acerca do mundo sem recorrer à experiência. Por exemplo, o facto de termos adquirido os conceitos de azul e de vermelho através da experiência perceptiva não nos impede de saber a priori que um objecto todo vermelho não pode ser azul.
Não se deve confundir as posições racionalistas tradicionais com a defesa de uma capacidade racional de intuição responsável pelo nosso conhecimento a priori. Por exemplo, como sabemos que ou chove ou não chove? Porque num certo sentido podemos “ver” através da nossa intuição racional que isso é verdade. Os primeiros grandes filósofos racionalistas foram Descartes, Leibniz e Espinosa. As posições racionalistas foram praticamente rejeitadas durante o séc. XIX com a descoberta de geometrias não euclidianas. Graças ao trabalho de filósofos como Thomas Nagel (n. 1937) e Laurence Bonjour (n. 1943) o racionalismo volta a estar hoje na ordem do dia.
2. Num sentido mais geral, o racionalismo é a ideia de que só racionalmente podemos chegar às verdades acerca do mundo. Tanto a experiência como a razão são métodos racionais de aquisição de conhecimento, por oposição aos processos místicos, como a fé ou a revelação divina. (Célia Teixeira)
Rawls, John (1921–2002)
Filósofo moral e político americano considerado o principal filósofo político do séc. XX. As ideias de Rawls inserem-se na tradição do contrato social de Locke, Rousseau e Kant. Rawls pensa que se as pessoas tiverem de escolher os princípios (ver princípio) de justiça sem saber como poderão ser por eles afectados, escolherão princípios justos. Imagina, assim, uma experiência mental em que todas as pessoas se encontram numa “posição original” sob um “véu de ignorância”, isto é, em que desconhecem quais as suas aptidões, posição social, riqueza, religião e concepção de valor e de bem. Nesta situação, pensa Rawls, as pessoas chegarão por um contrato social hipotético àquilo a que chama justiça como equidade. Esta concepção de justiça é expressa por dois princípios, um que garante liberdades básicas iguais (ver liberdade) para todos — como as políticas, de expressão e reunião, de consciência e de pensamento, etc. —, e outro que estabelece que as desigualdades devem ser distribuídas de forma a beneficiarem todos e que devem decorrer de posições e funções a que todos tenham acesso. Este último princípio implica que a riqueza seja distribuída de modo a fazer com que os que estão em pior situação fiquem tão bem quanto possível. Uma sociedade justa será liberal (ver liberalismo), democrática (ver democracia) e um sistema de mercado no qual se procede à distribuição da riqueza e em que pessoas com capacidades e motivações iguais têm possibilidades iguais de sucesso, independentemente da classe social em que tenham nascido. (Álvaro Nunes)
Kukathas, Chandran, et.al., Rawls: Uma Teoria da Justiça e os Seus Críticos (Lisboa: Gradiva, 1995).
Rawls, John, Uma Teoria da Justiça (Lisboa: Presença, 2001).
Rawls, John, O Liberalismo Político (Lisboa: Presença, 1997).
Rawls, John, A Lei dos Povos (Coimbra: Quarteto, 2000).
razão
A faculdade de raciocinar, compreender, ponderar, ajuizar, etc. Os filósofos dividem-se quanto à confiança que depositam na razão. Os mais cépticos duvidam dos seus produtos; alguns, como Hume, confiam mais nas emoções e sentimentos. Outros, como Descartes ou Kant, confiam mais no poder da razão para descobrir verdades importantes. A racionalidade instrumental permite, perante fins dados, determinar os melhores meios para os atingir; por exemplo, quando tenho sede e sei que há água na cozinha, um meio de matar a sede é ir à cozinha. A racionalidade não instrumental, negada por filósofos como Hume, permite determinar os próprios fins. (Desidério Murcho)
razão prática
Um raciocínio prático é um argumento cuja conclusão se refere à acção. Por exemplo: “Se quiser beber água, tenho de ir à cozinha; eu quero beber água; logo, tenho de ir à cozinha”. O raciocínio moral é uma parte própria do raciocino prático, referindo-se às acções moralmente relevantes: “Causar sofrimento aos animais é moralmente errado; consumir produtos de origem animal contribui para o sofrimento dos animais; logo, devo deixar de consumir produtos de origem animal”. Kant usava a expressão “razão prática” para se referir à faculdade humana que produz os raciocínios práticos. (Desidério Murcho)
razão pura
Expressão usada por Kant para se referir à faculdade responsável por produzir raciocínios inteiramente a priori, isto é, raciocínios cujas premissas são conhecíveis a priori. Ver a priori e a posteriori.
razão suficiente, princípio da
Princípio proposto por Leibniz. Numa das suas formulações, é a ideia de que todo o existente carece de uma explicação da sua existência: por que razão existe? Caso se trate de algo que existe, mas poderia não ter existido (um existente contingente), a resposta comum invoca outro existente: a Daniela existe porque os seus pais a conceberam, por exemplo. Mas caso se trate de algo que existe, mas não poderia não ter existido (um existente necessário), a resposta é simplesmente que não poderia não ter existido: Deus, se for um existente necessário, existe porque não poderia não existir. (Desidério Murcho)
realidade
A totalidade daquilo que há. O conceito de realidade gera uma polémica filosófica muito antiga e importante — o debate entre o realismo e o anti-realismo — em que se discute justamente o que há: deveremos incluir os números, os seres imaginários, as mentes alheias, os mundos possíveis, o passado e o futuro? Ou, pelo contrário, apenas as entidades do mundo actual e que têm uma existência espaciotemporal? Um filósofo realista defende que há aquelas “coisas” acerca das quais é realista. Mas ser realista acerca de uma certa classe de “coisas” não implica ser realista acerca de qualquer outra ou de todas as classes de “coisas" — podemos acreditar que há mentes independentes da nossa e não aceitar que haja seres imaginários. Ver abstracto e concreto, categorias, essência, existência, ontologia, ser e universais. (António Paulo Costa)
realismo
Vulgarmente diz-se que a atitude de uma pessoa é realista quando essa pessoa evita a especulação, agindo em função dos factos e não dos seus próprios desejos. Nas artes diz-se que um estilo é realista quando evita o ornamento e a fantasia, realçando a maneira como as coisas realmente são. Em filosofia o sentido é diferente, embora existam quase tantas variedades de realismo quantos os tópicos filosóficos em disputa: realismo conceptual, realismo ontológico, realismo epistemológico, realismo ético, realismo estético, realismo matemático, etc. Basicamente o que há em comum em todas estas formas de realismo é a afirmação da existência de algo independentemente do que pensamos, imaginamos, desejamos, acreditamos, sentimos, etc., a seu respeito. A ideia é a de que há coisas que têm uma existência real e independente da mente. Não há filósofos que defendam o realismo em todas as áreas, pois nem tudo parece ser independente da mente: sem mentes não haveria emoções. Já é mais frequente encontrarmos filósofos realistas em relação à ontologia e à epistemologia, mas recusarem o realismo ético (ou moral) e o realismo estético, por exemplo. Os principais tipos de realismo são os seguintes:
1. Realismo conceptual: o termo “realismo” começou por ser aplicado à doutrina de Platão acerca dos universais, de acordo com a qual os universais (a sabedoria, a triangularidade, a humanidade, etc.) são entidades reais e independentes, e não meros conceitos. A doutrina oposta é o nominalismo.
2. Realismo ontológico: esta é uma doutrina acerca do que existe e afirma que o mundo em que vivemos é independente de nós, podendo inclusivamente existir objectos que nunca serão apreendidos por nós. O anti-realismo é a teoria que se lhe opõe.
3. Realismo epistemológico: a perspectiva segundo a qual os objectos percepcionados por nós têm uma existência independente. Este tipo de realismo é dos mais conhecidos e discutidos e, consoante as teorias da percepção adoptadas, também existem diferentes tipos de realismo: o realismo directo (ou realismo ingénuo) e o realismo indirecto (ou realismo crítico). A perspectiva que se lhes opõe é o idealismo.
4. Realismo ético: a ideia de que há factos éticos como “matar é errado”, que não dependem dos nossos sentimentos ou emoções. A perspectiva oposta é o emotivismo.
5. Realismo estético: a ideia de que há factos estéticos, opondo-se às doutrinas subjectivistas que defendem que a beleza está nos olhos do observador. (Aires Almeida)
realismo crítico
A doutrina epistemológica de acordo com a qual o mundo exterior não é uma construção mental, mas que o nosso acesso a ele se dá indirectamente através de representações na nossa mente (ver representação). Por isso também é conhecido como realismo indirecto. Dado que as representações não são o mesmo que os objectos representados, o realista crítico conclui que os objectos não são exactamente como os percepcionamos. Assim, há características que dependem da maneira como a nossa percepção funciona (as qualidades secundárias) e outras que existem de forma independente nos próprios objectos (as qualidades primárias). Esta distinção está na base da concepção moderna de ciência e corresponde à distinção entre aparência e realidade. (Aires Almeida)
realismo directo
O mesmo que realismo ingénuo.
realismo estético
O mesmo que objectivismo estético.
realismo indirecto
O mesmo que realismo crítico.
realismo ingénuo
A crença, partilhada pela maior parte das pessoas, de que o mundo exterior existe e que é exactamente como o percepcionamos. A ideia é a de que entre nós e os objectos exteriores nada se interpõe; temos acesso directo a eles (por isso também é conhecido como realismo directo). Diz-se que é ingénuo porque passa ao lado de objecções óbvias como a possibilidade de termos ilusões ou de haver frequentemente diferenças na maneira como diferentes pessoas percepcionam os mesmos objectos (ou até a mesma pessoa ter experiências perceptivas diferentes acerca do mesmo objecto em momentos diferentes). (Aires Almeida)
realismo moral
Perspectiva metaética segundo a qual há factos morais e estes são objectivos (ver objectivo e subjectivo). Quem diz, por exemplo, que o aborto é errado, está a afirmar uma verdade ou uma falsidade independente de quaisquer gostos pessoais ou convenções sociais. Alguns realistas são naturalistas; outros são intuicionistas. Para os primeiros, os factos morais são apenas uma espécie de factos naturais, e como tal podem ser conhecidos através da observação; os segundos rejeitam esta ideia, sustentando que os factos morais só podem ser conhecidos por intuição intelectual. (Pedro Galvão)
redução ao absurdo
Um argumento com a seguinte forma: “P; de P segue-se um absurdo; logo, não P”. Por exemplo: “Eu não existo; mas se não existo, não posso estar a pensar isto, o que é falso, dado que estou evidentemente a pensar; logo, eu existo”. O absurdo que se segue da primeira premissa pode ser uma contradição com a forma “Q e não Q" — e na lógica formal tem de ser uma contradição. Mas na argumentação informal o absurdo pode ser apenas uma falsidade evidente, ou uma afirmação que de algum modo contradiz a primeira premissa: “Todas as verdades são relativas; mas isto é absurdo porque nesse caso essa mesma verdade seria relativa e, se for relativa, nem todas as verdades são relativas; logo, nem todas as verdades são relativas”. (Desidério Murcho)
reducionismo
1. Posição segundo a qual as verdades de uma área podem ser eliminadas e expressas como verdades de outra área. Por exemplo, quem defende a redução da química à física, defende que os fenómenos químicos mais não são do que fenómenos físicos. As reduções são metafisicamente (ver metafísica) importantes pois ajudam a perceber qual a realidade última do mundo. Por exemplo, se for possível reduzir todas as ciências à física, isso mostraria que a realidade última do mundo é física.
2. Num sentido popular, usa-se “reducionismo” no sentido pejorativo de redutor. Neste sentido, dizer que uma dada área é redutora significa que não dá conta de todos os aspectos da realidade. Este tipo de crítica corre, contudo, o perigo de ser ela própria redutora: dizer que algo é redutor sem mais argumentos é o mesmo que dizer que é mau porque é mau, o que, obviamente, não é uma crítica credível. Ver unidade da ciência. (Célia Teixeira)
reductio ad absurdum
Expressão latina que significa “redução ao absurdo”.
referência
A relação que um termo singular, como um nome, tem com aquilo que refere. Por exemplo, o nome “Eça de Queiroz” refere Eça de Queiroz. Entre os problemas relacionados com a referência contam-se o de saber como referem os termos aquilo que referem e o de saber como é possível referir objectos não existentes, como o Pai Natal. Ver filosofia da linguagem. (Célia Teixeira)
refutação
Refutar afirmações é diferente de refutar argumentos; mas em ambos os casos trata-se de mostrar que a afirmação ou o argumento, consoante o caso, é inaceitável. Uma afirmação como “toda a gente é infeliz” refuta-se apresentando um argumento ou um contra-exemplo. No caso de se apresentar um argumento, a sua conclusão terá de ser a negação do que se quer refutar, ou pelo menos inconsistente (ver inconsistência) com o que se quer refutar. Assim, para refutar que toda a gente é infeliz é necessário argumentar a favor de “algumas pessoas não são infelizes" (contraditória) ou “Nenhuma pessoa é infeliz" (inconsistente, admitindo que há pessoas). No caso de se apresentar um contra-exemplo, trata-se de apresentar uma pessoa que obviamente não seja infeliz. Só as afirmações universais podem ser refutadas por meio de contra-exemplos; as afirmações particulares não podem sê-lo. O modo como se refuta um argumento é diferente. A este respeito, ver contra-argumento. (Desidério Murcho)
regressão infinita
Dá-se uma regressão infinita quando uma explicação, definição ou argumento adia sucessivamente o que se pretendia explicar, definir ou defender. Por exemplo: “Onde está a Terra? Não pode estar suspensa no vazio, senão caía." “Quem a sustenta é Atlas, um grande deus poderoso." “E quem sustenta Atlas?" “Uma tartaruga." “E quem sustenta a tartaruga?" “Não sejas impertinente!” A célebre crítica de Bertrand Russell ao nominalismo (Os Problemas da Filosofia, cap. 9) baseia-se na ideia de que a explicação nominalista dos universais em termos de semelhança entre particulares implica uma regressão infinita. (Desidério Murcho)
relação causal
A relação que existe entre uma causa e um efeito. O tópico da causalidade é um dos mais importantes tópicos da metafísica, da epistemologia e da filosofia da ciência. Um dos problemas clássicos sobre este tópico é o de saber se as relações causais existem realmente, ou se apenas se trata de relações que a nossa mente atribui aos fenómenos que ocorrem conjuntamente. David Hume deu um dos contributos clássicos mais importantes para a discussão do problema. Ver causa e efeito e cadeia causal. (António Paulo Costa)
relativismo
A formulação tradicional do relativismo deve-se ao sofista Protágoras e afirma que “O homem é a medida de todas as coisas”, em particular das suas crenças. A interpretação mais natural deste princípio é a de que, se acreditamos que uma proposição é verdadeira, então essa proposição é verdadeira para nós, enquanto seres humanos; e que portanto a veracidade das nossas crenças não é absoluta, mas relativa ao nosso equipamento perceptivo e conceptual. Uma concepção na mesma linha, mas mais abrangente, é a aquela segundo a qual todo o conhecimento é relativo não só às particularidades cognitivas mas também às psicológicas, sociais, culturais e históricas de um dado agente. Segundo esta concepção, nenhuma proposição é verdadeira (ou falsa) em absoluto, mas apenas relativamente. Por outras palavras, o que é verdade para mim (devido a certos condicionalismos sociais ou psicológicos, por exemplo) pode ser falso para outra pessoa (condicionada de modo diferente), não havendo nenhum critério objectivo que permita decidir quem tem razão em absoluto. Apesar de ser bastante popular, quer entre os filósofos (designadamente nos meios “pós-modernos”) quer no senso comum, esta tese tem sérios problemas. Em primeiro lugar, contradiz uma ideia razoável acerca do que é ser verdadeiro e falso: em geral, se uma proposição for verdadeira, não é razoável dizer, de alguém que acredita que ela é falsa, que tem razão (para si próprio). A noção de verdade parece implicar a existência de critérios objectivos de aferição do verdadeiro e do falso; e isto acontece mesmo em casos onde não há consenso sobre quais são eles ou como devem ser aplicados (por exemplo, apesar de não ser consensual que Jorge Sampaio seja um bom Presidente, ou que a pena de morte deva ser permitida, não é razoável dizer que quer os adeptos quer os detractores de Jorge Sampaio ou da pena de morte têm razão para-si-próprios — mas antes que não é neste momento possível estabelecer sem margem para dúvidas quem tem razão). Além disso se, em vez de admitirmos que algumas verdades são relativas — por exemplo, as respeitantes ao gosto estético ou, mais trivialmente, ao gosto gastronómico —, defendermos que todas são, então a própria proposição de que todas as verdades são relativas terá, ela própria, de ser verdadeira relativamente. Mas, se assim for, ela será, com igual legitimidade, falsa para quem estiver condicionado para discordar dela. Ora, o relativista, como seria de esperar, pretende que a sua tese seja absolutamente verdadeira (e que a sua negação seja absolutamente falsa). Para escapar a esta dificuldade, ele poderia argumentar que essa tese é a única que escapa ao relativismo universal; mas teria então de explicar o que legitima um tal tratamento de excepção.
Costuma-se associar o relativismo à ideia de tolerância para com os pontos de vista alheios (o que, em grande medida, ajuda a explicar a sua popularidade). Esta associação é, porém, um equívoco — pois podemos admitir, e até promover, a livre expressão de opiniões diferentes da nossa ao mesmo tempo que as consideramos (absolutamente) falsas. Ver também objectivismo e subjectivismo, pragmatismo, relativismo ético. (Pedro Santos)
relativismo moral
Teoria metaética segundo a qual os factos morais são instituídos pela sociedade e, portanto, podem variar de sociedade para sociedade ou de época para época. Se numa sociedade a maior parte das pessoas acredita, por exemplo, que a pena de morte é justa, então nessa sociedade a pena de morte é justa, mas se noutra sociedade a maioria acreditar que a pena de morte é injusta, então aí a pena de morte é efectivamente injusta. Para o relativista, os juízos morais limitam-se a reflectir certos costumes sociais. Quando os costumes ou as crenças morais de uma sociedade mudam, também os factos morais se alteram. (Pedro Galvão)
religião, filosofia da
Ver filosofia da religião.
reminiscência
O mesmo que anamnese.
representação
Designação dada, na teoria representativa da percepção, aos conteúdos da consciência (dados dos sentidos, sensações e ideias) que supostamente os objectos exteriores causam em nós e por intermédio dos quais os conhecemos. Segundo os defensores da teoria (Locke, por exemplo), esses conteúdos são imagens mentais mais ou menos adequadas dos objectos exteriores. Contudo, os críticos (entre os quais se encontra Berkeley) têm chamado a atenção para a dificuldade em ligar essas representações, internas e subjectivas (ver objectivo e subjectivo), com os objectos representados, externos e objectivos, e para o facto de a teoria a abrir assim as portas ao cepticismo. Ver ideia, percepção, realismo, qualidades primárias e secundárias. (Álvaro Nunes)
res cogitans
Latim: “coisa pensante”. Descartes usa o termo para referir o agente que pensa, a coisa que faz o pensamento, de cuja existência é impossível duvidar e que difere do sujeito físico. (Desidério Murcho)
responsabilidade
Ser responsável por uma acção ou por uma omissão significa ser passível de responder por ela — por exemplo, perante os pais ou perante um tribunal. No senso comum e na tradição filosófica, religiosa e jurídica, a responsabilidade, seja legal ou moral, é vista como uma consequência do livre-arbítrio: somos responsáveis pelas nossas acções porque somos livres. A responsabilidade não é apenas individual — por exemplo, ao estado é atribuível uma responsabilidade colectiva. Alguns filósofos defenderam a doutrina da responsabilidade negativa, segundo a qual somos responsáveis não só pelos acontecimentos que provocámos, mas também pelos acontecimentos que poderíamos ter evitado. Ver ininputabilidade. (António Paulo Costa)
retórica
1. O estudo do uso persuasivo da linguagem. Os estóicos integraram o estudo da retórica na lógica, e hoje em dia é mais comum chamar-lhe lógica informal.
2. O uso de técnicas persuasivas mas enganadoras, como quando alguém profere um discurso racista inflamado, que não se baseia em argumentos sólidos nem informação fidedigna, mas em sugestões falaciosas e em informação deficiente.
3. O uso literariamente elegante da linguagem persuasiva. (Desidério Murcho)
Rorty, Richard (1931–2007)
Filósofo norte-americano, influente também nos estudos literários. Os seus heróis filosóficos encontram-se na filosofia analítica (Wittgenstein, Sellars, Davidson) e continental (Hegel, Heidegger, Derrida), mas a figura central é Dewey.
São duas as obras principais: Philosophy and the Mirror of Nature (1979) e Contingency, Irony, and Solidarity (1989). Considerando a ubiquidade da linguagem, PMN defende que levar os pressupostos da filosofia analítica até às últimas consequências significa questionar a imagem da mente como espelho da natureza e do conhecimento como representação. Se não podemos sair da linguagem para verificar a exatidão das nossas descrições, mais vale abandonarmos a ideia de representação exata. O seu mais polémico contributo reconsidera a noção de verdade como uma questão de consenso – solidariedade – e não de objetividade.
Dedica-se depois às consequências, sobretudo políticas, de uma posição antirepresentacionista. Em CIS abandona a tentativa de unificar público e privado: os cidadãos da sua utopia política seriam liberais – avessos à crueldade – e ironistas – conscientes da contingência do seu vocabulário final. Tido como filósofo-do-fim-da-Filosofia, defende uma cultura pós-filosófica, literária ou pragmatista, em que os valores de Verdade, Objetividade e Realidade dariam lugar a uma sociedade mais liberal, solidária e democrática. (Patrícia Fernandes)
Russell, Bertrand (1872–1970)
Filósofo inglês. Nasceu no seio de uma família aristocrata. Foi educado por preceptores até ingressar no Trinity College de Cambridge para estudar matemática. Russell teve uma vida longa e controversa. As suas preocupações sociais levaram-no ao activismo político, tendo participado, por exemplo, em movimentos sufragistas e em campanhas contra a guerra e pelo desarmamento nuclear. Chegou a ser preso durante uma dessas campanhas. As suas preocupações educacionais levaram-no a escrever muitos livros dirigidos ao grande público. Em 1950 recebeu o Prémio Nobel da literatura.
As suas preocupações com os fundamentos da matemática resultaram na publicação do monumental Principia Mathematica (1910–13), o qual consiste em três volumosos livros escritos com a colaboração Alfred Whitehead (1861–1947). O objectivo era reduzir a lógica à matemática (ver reducionsimo). Os instrumentos lógicos descobertos e desenvolvidos por Russell (e simultaneamente por Frege), permitiram-lhe abordar alguns problemas filosóficos intrincados iniciando uma forma de fazer filosofia que influenciou muito Carnap e os restantes positivistas lógicos. No seu famoso artigo “On Denoting" (1905), Russell usou esses instrumentos para resolver o problema de saber como podemos falar com sentido de algo que não existe. Dessa resposta resultou a sua famosa teoria das descrições definidas. Russell defendeu que frases como “O actual rei de França é careca”, em que a descrição definida “o actual rei de França” nada refere (ver referência), são falsas. Em epistemologia, distinguiu duas formas de conhecimento: temos conhecimento por contacto quando estamos em contacto com uma coisa ou uma pessoa e temos conhecimento por descrição quando conhecemos algo através de uma descrição. Defendeu o atomismo lógico, uma forma extrema de empirismo. Em metafísica, Russell era realista, defendendo a existência de universais. É autor de Os Problemas de Filosofia (1912, trad. Desidério Murcho, 2008), um livro de introdução que se tornou leitura obrigatória para muitos estudantes de filosofia, e de uma das mais influentes histórias da filosofia, a História da Filosofia Ocidental (1945, trad. Círculo de Leitores, 1977), entre muitas outras obras. (Célia Teixeira)
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 21 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 14 (Lisboa: Presença, 1989).
S
S. Tomás de Aquino
Ver Tomás de Aquino.
saber
O mesmo que conhecer. Ver conhecimento, opinião.
salva veritate
Expressão latina que significa “mantendo a verdade”. Usa-se a expressão em filosofia da linguagem para referir os contextos linguísticos em que se pode substituir uma expressão por outra “mantendo a verdade" (os chamados contextos “extensionais”). (Desidério Murcho)
Santo Agostinho (354-430)
Filósofo cristão que realiza a síntese entre a filosofia antiga de inspiração platónica e o cristianismo. Nas Confissões (c. 400; trad. 2001, INCM) descreve a sua conversão à fé cristã. Quanto à relação entre razão e fé afirma na Doutrina Cristã que a reflexão filosófica parte das verdades reveladas pelas Sagradas Escrituras e deve esclarecê-las. Repudiar a razão, crer sem compreender, é rejeitar um dom de Deus. A filosofia é um meio para a plena fruição da fé. Desafio para a fé e para a razão é o problema do mal. Não podendo ser criado por Deus, Supremo Bem, o mal é uma deficiência da vontade humana que prefere bens inferiores ao Criador. Marcada pelo pecado original, a vontade só com a intervenção da Graça divina pode fazer o bem. O amor das coisas efémeras e o desprezo do que é eterno deram origem à cidade terrestre em radical oposição à Cidade de Deus (411; trad. 1991, FCG). A história é o palco da luta entre estes dois reinos. O triunfo da cidade celeste consistirá na criação de uma comunidade universal de justos e fraternos vivendo segundo a lei e o amor de Deus. (Luís Rodrigues)
Sartre, Jean-Paul (1905–1980)
Filósofo, dramaturgo, romancista e militante político francês cuja obra desenvolve essencialmente uma tese: o homem é liberdade e define-se pelo que faz. No ser humano, a existência precede a essência, afirma Sartre em O Existencialismo é um Humanismo (1946; trad. 1970, Presença). Quer dizer: não há qualquer ideia que se possa fazer sobre um homem antes de ele existir e agir porque não há qualquer modelo pré-definido, nenhum destino previamente traçado. A radical afirmação da liberdade humana exige a negação da existência de Deus (em O Ser e o Nada (1643) diz que Deus é uma paixão inútil). Não existe Deus para nos dizer o que fazer e como viver. A liberdade humana é o fundamento de todos os valores e exige do ser humano um compromisso permanente, uma renovação constante por meio de escolhas e actos, porque é o nosso modo de ser como sujeitos conscientes. O existencialismo de Sartre é um humanismo porque afirma depender do homem ser o senhor do seu destino. (Luís Rodrigues)
Searle, John
(n. 1932) Filósofo da linguagem e da mente. Foi aluno de J. L. Austin em Oxford, nos anos 50, sendo professor na Universidade da Carlifórnia em Berkeley até aos dias de hoje. Em filosofia da linguagem, Searle defende que as entidades básicas a analisar não são expressões linguísticas pertencentes a uma dada língua (por exemplo, frases dessa língua), mas produções ou elocuções de tais expressões (ou seja, actos de fala). Estas produções de sequências linguísticas (subentende-se, gramaticais e com sentido) são regidas por regras, sendo felizes (felicitous) ou infelizes segundo obedeçam a essas regras ou as infrinjam (uma noção que Searle herdou de Austin). A aprendizagem de uma língua pode, por sua vez, ser vista, em última análise, como a aprendizagem de tais regras, descritas pela teoria searleana dos actos de fala. Uma vez que a concepção searleana da linguagem humana está comprometida com a ideia de que falar é praticar acções, essa descrição faz parte de uma teoria mais geral acerca do modo como a mente humana opera na sua relação com o mundo — sendo a filosofia da linguagem, desta perspectiva, um ramo da filosofia da mente. Searle dedica o seu trabalho mais recente sobretudo a esta última disciplina, e em particular à defesa da tese de que os estados mentais são essencialmente intencionais, o que o opõe a perspectivas como o comportamentalismo e o funcionalismo. A sua famosa experiência mental do quarto chinês é frequentemente considerada um argumento convincente a favor da ideia de que a manipulação não consciente e, logo, não intencional de informação codificada, como a que é tipicamente executada por um computador, não corresponde a um processo mental — algo que por vezes se formula sugestivamente dizendo-se que a experiência mostra que “os computadores jamais poderão pensar”. (Pedro Santos)
Searle, John, Intencionalidade (Lisboa: Relógio D'Água, 2007).
Searle, John, Mente, Cérebro e Ciência (Lisboa: Edições 70, 2005).
Searle, John, Actos de Fala (Coimbra: Livraria Almedina, 2006).
Searle, John, A Redescoberta da Mente (Lisboa: Instituto Piaget, 1998).
semântica
1. O ramo da linguística que estuda o significado literal das expressões linguísticas e a sua relação com a realidade extralinguística. Uma teoria com grande aceitação é a de que uma das tarefas principais da semântica consiste em definir as condições de verdade das frases de uma língua natural e em explicar como essas condições de verdade resultam, por um lado, dos significados parciais das expressões que compõem essas frases e, por outro, da sua estrutura sintáctica (ver sintaxe). Outras tarefas tipicamente associadas à semântica são a de especificar as diferentes componentes do significado das expressões linguísticas (por exemplo, o seu sentido e a sua referência) e a de relacionar sistematicamente o significado das frases com o seu potencial inferencial (ou lógico). Alguns tópicos abrangidos pela semântica (por exemplo significado, verdade, referência) são comuns à filosofia da linguagem, de modo que não existe uma fronteira nítida entre as duas disciplinas. É, porém, razoável dizer que a semântica dá ênfase ao estudo empírico das línguas naturais, ao passo que a filosofia da linguagem se dedica sobretudo à análise dos conceitos necessários para esse estudo.
2. A semântica de uma linguagem formal (ver cálculo lógico) resulta da atribuição de significados aos seus símbolos básicos e fórmulas, as quais recebem um valor de verdade — ver interpretação. No cálculo de predicados, por exemplo, isto permite ver quais as derivações admitidas pela sintaxe da linguagem que são válidas. Ver também pragmática. (Pedro Santos)
senciência
Os seres sencientes têm a capacidade de sentir prazer ou dor. Assim, havendo senciência, há alguma vida mental consciente que pode ser melhor ou pior para quem a vive. As plantas não são sencientes; a grande maioria dos animais, entre os quais nos incluímos, são-no. De acordo com os defensores do utilitarismo, todos os seres sencientes — e só eles — têm estatuto moral. Não têm, no entanto, o mesmo estatuto: devemos ter uma maior consideração moral por aqueles que possuem uma vida mental mais rica e complexa. Na ética deontológica de Kant, pelo contrário, entende-se que muitos dos seres sencientes não têm estatuto moral: só devemos uma consideração moral directa aos seres dotados de uma natureza racional. (Pedro Galvão)
sensibilidade
1. Mais vulgarmente refere a disposição para valorizar de modo especial as atitudes e as emoções. A doutrina ética do emotivismo, por exemplo, dá um relevo especial a este tipo de disposição das pessoas.
2. Em estética, sensibilidade significa o mesmo que refinamento do gosto.
3. Em epistemologia, particularmente na filosofia de Kant, a sensibilidade é a capacidade perceptiva do sujeito que, apoiada nos órgãos dos sentidos, fornece a matéria para o conhecimento. (Aires Almeida)
sensível, mundo
Ver mundo sensível.
senso comum
O conjunto mais alargado de crenças que uma comunidade tem por verdadeiras e partilha durante um certo período de tempo. O senso comum é um “saber” que resulta da experiência de vida individual e colectiva. Os hábitos e costumes, as tradições e rituais, os “ditos” e provérbios, as opiniões populares, etc., são habitualmente referidos como manifestações do senso comum. A sua aprendizagem é uma condição necessária para a socialização de cada membro da comunidade, funcionando como um mecanismo regulador do seu pensamento e da sua acção. Do ponto de vista da ciência e da filosofia, os processos de justificação das crenças de senso comum afiguram-se muitíssimo superficiais e falíveis, e é frequente tais crenças resistirem mal a um exame crítico mais minucioso, pelo que a sua ampla aceitação não é uma garantia de que sejam verdadeiras. Alguns filósofos têm discutido a continuidade e descontinuidade entre o senso comum e a ciência e a filosofia, tendo particular relevância, nessa discussão, o problema da demarcação. Ver crença, verdade e falsidade, crítica, critério de demarcação. (António Paulo Costa)
sentido
Aquilo que uma pessoa associa a uma expressão quando a compreende. Frege distinguiu o sentido de uma expressão da sua referência no seu famoso artigo “Über Sinn und Bedeutung" (“Sobre o Sentido e a Referência”, 1892). Duas expressões podem referir o mesmo objecto mas ter diferentes sentidos. Por exemplo, as expressões “Estrela da Manhã” e “Estrela da Tarde” referem a mesma coisa, nomeadamente, Vénus, mas têm sentidos diferentes (têm diferentes modos de apresentação). Esta distinção está intimamente relacionada com a distinção entre conotação e denotação, e entre intensão ou compreensão e extensão. Ver filosofia da linguagem. (Célia Teixeira)
sentido da existência
Ver sentido da vida.
sentido da vida
Em geral, dizemos que uma certa actividade é absurda ou não tem sentido quando não tem qualquer objectivo. Por exemplo, não faz sentido passar a vida aos saltos se isso não tiver qualquer objectivo; mas faz sentido, se o objectivo for exercitar os músculos. Em geral, dizemos também que uma certa actividade não tem sentido, apesar de ter um objectivo, se esse objectivo não puder ser alcançado ou não tiver qualquer valor, mesmo que possa ser alcançado. Por exemplo, não faz sentido passar a vida a tentar chegar à Lua a saltar, porque nunca o iremos conseguir; e não faz sentido passar a vida a tentar fazer passar um elefante por debaixo da porta da cozinha, não só porque nunca o vamos conseguir, mas também porque, mesmo que o conseguíssemos, isso não teria aparentemente importância alguma.
Assim, responder ao problema do sentido da vida é responder às seguintes três perguntas: Terá a vida humana, no seu todo, um ou vários objectivos? Será esse objectivo (ou objectivos) alcançável? Terá esse objectivo (ou objectivos) algum valor? A resposta da maior parte dos filósofos consiste em dizer que o objectivo da vida humana é a felicidade; mas depois diferem no modo como entendem o que constitui a felicidade. As tradições religiosas defendem em geral que a vida só faz sentido se Deus existir; alguns filósofos aceitaram esta ideia, mas acrescentaram que a vida absurda tem de ser então abraçada precisamente porque Deus não existe (ver existencialismo). Contudo, muitos filósofos não concebem o sentido da vida como algo que dependa da existência ou não de Deus, e é costume chamar “humanista” a esta tradição. (Desidério Murcho)
sentidos, dados dos
Aquilo que apreendemos pelos sentidos e sem recorrer à inferência. Os dados dos sentidos são, assim, os objectos imediatos da percepção. Diz-se que os objectos são “imediatos” precisamente porque não se obtêm por inferência. Por exemplo, quando olho para o livro amarelo que está à minha frente apreendo sem recorrer à inferência uma certa cor e uma certa forma. Esta cor e esta forma não podem ser confundidas com o objecto físico — o próprio livro — que acredito estar diante de mim, pois é possível duvidar da existência do livro mas não duvidar dos dados dos sentidos. Por isso dizemos que há diferença entre aparências e realidade. Ainda que não exista qualquer livro, eu tenho consciência de alguma coisa amarela. Assim, os dados dos sentidos são as entidades, sejam elas quais forem e seja qual for a sua natureza (física ou mental), que estão directamente perante a mente. A expressão foi introduzida por Russell, mas filósofos como Locke, Berkeley e Hume utilizavam de modo semelhante as expressões “ideias dos sentidos”, “qualidades sensíveis” e “impressões dos sentidos”, respectivamente, para referir os objectos da percepção. Dependendo da teoria da percepção adoptada, as opiniões dos filósofos divergem quanto ao tipo de relação que os dados dos sentidos têm com os objectos físicos. Os filósofos empiristas dão uma importância especial aos dados dos sentidos, pois encontram neles o fundamento para o conhecimento empírico. Note-se que os dados dos sentidos não constituem, em si, conhecimento proposicional. (Aires Almeida)
ser
O verbo “ser” é claramente ambíguo, podendo ter, entre outros, os seguintes significados: 1) atributivo, como em “O João é alto”; 2) identitativo, como em “O João é o amante secreto da Ana”; 3) constitutivo, como em “Esta mesa é de madeira”; 4) inclusivo, como em “As baleias são mamíferos”; e, mais exoticamente, 5) existencial, com em “Deus é”. Confundir estes usos pode dar origem a afirmações sem sentido ou a falácias (por exemplo, de “As baleias são mamíferos” não se pode inferir que o conjunto das baleias é idêntico ao conjunto dos mamíferos). A questão de saber o que é ser ou existir e que tipos de coisas realmente existem (será que os números, ou as proposições, ou Deus, existem?) é uma questão metafísica perene. Esta questão foi por vezes distinguida da questão de saber quais as entidades que usufruem de um modo especial de ser, caracterizado pela consciência da sua própria existência e pela liberdade de escolha (ver existencialismo). Foi também distinguida da questão de saber como caracterizar esse exemplar único de um tipo de entidade primordial, o Ser (não necessariamente identificável com Deus), fonte da existência de todos os “entes”. Este tipo de preocupação, típica de filósofos como Heidegger, foi alvo de objecções por parte, sobretudo, de filósofos da tradição analítica (ver filosofia analítica). A crítica mais comum é a de que, sendo “ser” um verbo, ele só pode ser usado como tal (por exemplo, numa das várias acepções mencionadas acima), e que o seu uso como substantivo (com ou sem maiúscula) dá origem a frases sem sentido e portanto a equívocos filosóficos. Ver também existência. (Pedro Santos)
significado
Aquilo que é compreendido quando algo nos é comunicado através de sons ou inscrições. Por exemplo, quando ouvimos a palavra “água” processamos esse som relacionando-o com a coisa que essa palavra refere (ver referência), nomeadamente, a água. O que isto sugere é que o significado de uma expressão é de algum modo composto por dois elementos: aquilo que se passa em nós quando apreendemos a expressão e aquilo de que a expressão fala. Muito se tem discutido sobre como funcionam esses dois componentes, se é que existem. A questão de saber o que é o significado é uma das questões centrais da filosofia da linguagem. (Célia Teixeira)
silogismo
Nome dado aos argumentos estudados pela lógica aristotélica compostos unicamente por duas premissas e uma conclusão. Por exemplo: “Todos os mortais são infelizes; todos os homens são mortais; logo, todos os homens são infelizes”. Por vezes, usa-se a expressão “silogismo" como sinónimo de “argumento” ou “raciocínio”. Ver lógica aristotélica. (Desidério Murcho)
símbolos lógicos
Expressões usadas para abreviar certos aspectos relevantes para a determinação da forma lógica. Por exemplo, no cálculo proposicional usa-se os símbolos P, Q, R, etc., como abreviaturas de proposições e como abreviatura de “Se…, então…”. Toda a lógica formal precisa de símbolos. Isto porque a lógica formal estuda aqueles argumentos cuja validade depende inteiramente da sua forma lógica; e para exibir a forma lógica de um argumento é necessário usar símbolos. Assim, na lógica aristotélica, por exemplo, é necessário exibir a forma lógica das proposições universais afirmativas, o que se pode fazer recorrendo a letras que simbolizam classes: em “todo o A é B” A e B simbolizam qualquer classe. Assim, uma afirmação como “todos os homens são mortais" tem a forma de uma universal porque se substituirmos “homens” por A e “mortais” por B obtemos “todos os A são B”, que é apenas uma variação gramatical logicamente irrelevante de “todo o A é B”. É na lógica clássica, contudo, que a formalização é mais profunda e sistemática. Ao passo que na lógica aristotélica se formaliza geralmente apenas os nomes das classes, na lógica clássica é mais comum formalizar tudo. Contudo, é falso que exista algo de intrinsecamente formal ou simbólico na lógica clássica que não existe na lógica aristotélica, pois tanto se pode formalizar completamente a lógica aristotélica, como se pode formalizar apenas parcialmente a lógica clássica. Ver Apêndice: Símbolos lógicos. (Desidério Murcho)
Singer, Peter (n. 1946)
Filósofo utilitarista (ver utilitarismo) nascido na Austrália que, influenciado por Hare, contribuiu decisivamente para o florescimento da ética aplicada. No âmbito da bioética, Singer discutiu muitos problemas rejeitando a perspectiva da santidade da vida humana, segundo a qual toda a vida humana, seja qual for a sua qualidade, tem um valor absoluto. Recusando o especismo (isto é, a discriminação baseada na espécie), Singer defendeu que os interesses dos animais têm de receber a mesma consideração que os interesses dos seres humanos e, com o seu livro Libertação Animal (1975; trad. 2000, Via Óptima), impulsionou o movimento de defesa dos animais. Entre as suas obras mais importantes contam-se também Ética Prática (1993; trad. 2000, Gradiva) e Um Só Mundo (2002; trad. 2003, Gradiva). (Pedro Galvão)
Sinn
Termo alemão que significa “sentido” e se opõe a “referência”. Frege introduziu esta distinção para separar o que um termo refere da maneira como o termo refere: os termos “Mestre de Platão” e “O filósofo que bebeu a cicuta” referem a mesma coisa (Sócrates), mas referem essa coisa de maneiras diferentes: têm diferentes sentidos. (Desidério Murcho)
sintaxe
1. O sistema de regras de geração das frases gramaticais de uma língua (consideradas como manifestações gráficas ou fonéticas de estruturas de palavras). O termo designa também o ramo da linguística que estuda esses sistemas. Questões tipicamente associadas aos estudos sintácticos são as de saber que regras são infringidas pelas frases agramaticais (como “férias estive de Agosto em”) e qual a estrutura das frases gramaticais.
2. O vocabulário e as regras de formação das fórmulas de uma linguagem formal (por exemplo, a do cálculo de predicados). Num cálculo lógico, essas fórmulas são por sua vez usadas em derivações, segundo certas regras de inferência. (Pedro Santos)
Sócrates (c. 469-399 a. C.)
Uma das figuras mais carismáticas e enigmáticas da história da filosofia. Embora nada tenha escrito, a sua influência é enorme e é responsável pela viragem da filosofia das questões da natureza para as questões humanas. Pouco mais se sabe acerca da sua vida, para além de que participou na guerra do Peloponeso e foi condenado à morte sob a acusação de impiedade e de corromper a juventude. Também se sabe pouco acerca do seu pensamento, embora seja a figura central de muitos diálogos de Platão, uma vez que é difícil diferenciar o Sócrates histórico da personagem platónica. Para Sócrates, a filosofia é um modo de vida e, por isso, fazia filosofia na ágora (praça pública), no ginásio ou nas ruas de Atenas, dialogando com aqueles que estivessem dispostos a investigar com ele um qualquer conceito moral. Começava por pedir ao seu interlocutor a definição de uma virtude, como a justiça, e depois, por intermédio de perguntas e respostas, levava-o a chegar a uma conclusão contraditória (ver contradição) com a definição que tinha apresentado. Com este método de refutação (elenchus) procurava mostrar àqueles que pretendiam ser sábios que as suas crenças (ver crença) eram inconsistentes (ver inconsistência) e, deste modo, levá-los a formular crenças mais adequadas. Apesar de afirmar não saber as respostas às questões que punha sobre as definições, há algumas ideias que parece ter assumido. As mais importantes são que a virtude, embora não possa ser ensinada, é conhecimento; que ninguém faz o mal (ver mal moral) voluntariamente; que não se pode fazer mal a um homem bom; que é pior fazer do que sofrer o mal; e que todas as virtudes se reduzem a uma, o conhecimento do que é e não é bom para um ser humano. Ver dialéctica, ética das virtudes, ironia, maiêutica. (Álvaro Nunes)
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 3 (Lisboa: Temas e Debates, 1999).
Magee, Brian, Os Grandes Filósofos, cap. 1 (Lisboa: Presença, 1989).
Platão, Êutifron, Apologia de Sócrates, Críton (Lisboa: INCM, 1993).
Platão, Laques, (Lisboa: Edições 70, 1989).
Platão, Hípias Maior (Lisboa: Edições. 70, 2000).
Platão, Hípias Menor (Coimbra: INIC, 1990).
Platão, Cármides (Coimbra: INIC, 1988).
Platão, Lísis (Coimbra: INIC, 1990).
Platão, Íon (Lisboa: Editorial Inquérito, 1988).
sofisma
Uma falácia apresentada com o intuito de enganar o interlocutor. (Desidério Murcho)
sofistas
Nome dado por Platão a um conjunto de professores de retórica da Grécia antiga. Platão e outros filósofos antigos acusavam os sofistas de falta de honestidade intelectual, afirmando que davam mais atenção à persuasão irracional do que à procura da verdade. Contudo, pelo menos alguns sofistas foram filósofos e cientistas destacados, assim como oradores ilustres. Antifonte (c. 480–411 a. C.), Górgias de Leontinos (c. 483–376 a. C.), Hípias (c. 485-415 a. C.) e Protágoras de Abdera (c. 490–c. 420 a. C.) foram alguns dos mais ilustres sofistas. (Desidério Murcho)
solipsismo
1. Em epistemologia é a perspectiva segundo a qual nada posso conhecer a não ser os meus próprios conteúdos mentais, dado que só a eles tenho acesso directo. O solipsista nega assim a possibilidade de conhecer outras coisas além de si próprio: não posso saber que ao meu lado está uma janela; tudo o que sei é que tenho na minha mente a ideia ou imagem da janela, o que é bem diferente.
2. Em ontologia, é a perspectiva relacionada com a anterior, mas mais radical, de que apenas eu e as minhas próprias experiências são reais. Os objectos físicos e as outras mentes não têm existência a não ser na minha mente. Os críticos sublinham que, na prática, ninguém se comporta como um verdadeiro solipsista. (Aires Almeida)
stoa
Termo grego que significa “pórtico” e que deu o nome ao estoicismo porque os estóicos ensinavam sob um pórtico. (Desidério Murcho)
Stuart Mill, John
Ver Mill, John Stuart.
subjectivismo
Ver objectivismo e subjectivismo.
subjectivismo estético
Doutrina acerca da justificação dos juízos estéticos, de acordo com a qual juízos como “x é belo” exprimem apenas os nossos sentimentos ou emoções pessoais acerca de x, independentemente de quaisquer características de x. Assim, o juízo estético, sendo subjectivo, nada mais é do que um juízo de gosto, uma vez que se limita as exprimir as nossas preferências. Kant e Hume, embora com algumas diferenças importantes, são partidários do subjectivismo estético, ao qual se opõe o objectivismo estético. (Aires Almeida)
subjectivismo moral
Teoria metaética segundo a qual os factos morais são subjectivos (ver objectivo e subjectivo). Segundo o subjectivista, quem diz, por exemplo, “O aborto é errado”, está na verdade a dizer algo como “Eu reprovo o aborto”. Assim, para o subjectivista os juízos morais descrevem apenas atitudes pessoais de aprovação ou reprovação. Ver emotivismo. (Pedro Galvão)
sublime
Uma das duas grandes categorias, juntamente com o belo, da estética do séc. XVIII. A experiência do sublime dá-se, supostamente, quando presenciamos espectáculos naturais como montanhas rasgando os céus e tempestades no mar. Trata-se de algo invulgarmente grandioso e fascinante, que só se manifesta perante objectos que ultrapassam e desafiam os limites da nossa imaginação, impondo respeito e, até, intimidando-nos com a sua majestade. Nesse sentido distingue-se claramente do belo. Kant considera que o sentimento do sublime nos confronta com a nossa pequenez, obrigando-nos a elevar acima da vulgaridade. Entretanto, praticamente deixou de se dar importância à noção de sublime e quase não é referida na estética contemporânea. (Aires Almeida)
substância e acidente
Segundo Aristóteles o que existe pode ser de dois modos: ou como substância ou como acidente. A substância é o que existe em si e não num outro ser (independência ontológica) e por isso não é dita de um sujeito mas é sujeito de outras coisas. O acidente é o que existe num outro ser, numa substância, como sua propriedade ou característica (será predicado de um sujeito). Assim, os acidentes não possuem um ser próprio (dependência ontológica). Dependem do ser da substância porque são algo que sucede ou acontece a esta. João, indivíduo concreto, não é algo que exista num outro indivíduo, tem um ser próprio, não é propriedade de outra coisa. O peso do João já é um acidente porque só existe como medida do corpo do João e não em si. A teoria aristotélica da substância é exposta em Categorias e na Metafísica, livros VII a IX. Ver também ontologia. (Luís Rodrigues)
T
tabela de verdade
Dispositivo gráfico que permite exibir as condições de verdade de uma forma proposicional dada (não se aplica a formas predicativas ou quantificadas). As condições de verdade são as circunstâncias em que uma dada afirmação é verdadeira ou falsa. Por exemplo, mesmo que não se saiba se a afirmação “Deus existe e a vida faz pleno sentido” é verdadeira ou não, sabe-se que só será verdadeira caso as duas afirmações componentes (“Deus existe” e “A vida faz pleno sentido”) sejam verdadeiras. Assim, as condições de verdade da afirmação original podem resumir-se numa tabela. Para isso, isola-se a forma lógica da afirmação, que neste caso é “P e Q”. E agora constrói-se uma tabela de verdade:
| P Q | P e Q |
| V V | V |
| V F | F |
| F V | F |
| F F | F |
As filas da tabela exibem as condições de verdade de “P e Q”: caso P seja verdadeira (V) e Q também, a frase é verdadeira; em todos os outros casos a frase é falsa (F). As tabelas de verdade permitem assim exibir as condições de verdade dos operadores verofuncionais.
Mas permitem também determinar se uma afirmação, complexa ou não, é uma verdade lógica (ver tautologia), uma falsidade lógica (ver contradição) ou uma contingência lógica. Só devolve resultados correctos quando se aplica a afirmações cuja verdade, falsidade ou contingência lógicas resultam exclusivamente da sua forma proposicional verofuncional. Por exemplo, para saber se a afirmação “Se Sócrates era um homem, era um homem” é uma verdade lógica começa-se por captar a forma lógica da afirmação, que é a seguinte: “Se P, então P”. Agora, faz-se uma tabela de verdade:
| P | Se P, então P |
| V | V |
| F | V |
Conclui-se que a afirmação é uma verdade lógica porque não há qualquer circunstância em que a afirmação seja falsa. Se não fosse uma verdade lógica, não seria verdadeira em todas as circunstâncias. Ver inspector de circunstâncias. (Desidério Murcho)
tábua rasa
Nome por que é conhecida a analogia utilizada por Aristóteles, mas por vezes também associada ao filósofo empirista inglês John Locke para ilustrar a ideia de que todo o conhecimento tem origem na experiência. Locke compara a nossa mente a uma folha de papel em branco, ou a uma superfície completamente lisa e sem qualquer sinal nela inscrito (“tabula rasa”, em latim), mas onde as impressões colhidas do exterior pelos nossos sentidos deixam as suas marcas. É a partir dessas impressões — que a nossa mente se limita a organizar — que se formam todas as ideias, mesmo as mais abstractas. Não há, pois, conhecimentos a priori nem ideias inatas. Todo o conhecimento é adquirido através dos sentidos. Ver também empirismo, a priori e a posteriori. (Aires Almeida)
tabula rasa
Expressão latina que significa tábua rasa.
tautologia
Em termos correntes, uma tautologia é uma proposição sem qualquer valor informativo, como “Todos os gatos são gatos”. Mas em lógica usa-se este termo para qualquer forma proposicional logicamente verdadeira, o que inclui formas extraordinariamente informativas e complexas. Neste sentido, uma tautologia é apenas uma proposição verdadeira cuja verdade depende inteiramente da sua forma lógica, como a forma {(Q ∨ P) ∧ [(¬R → ¬P) ∧ (S ∨ ¬Q)]} → (¬S → R). Uma forma de determinar se uma dada forma proposicional é uma tautologia é construir uma tabela de verdade: a forma é tautológica se, e só se, resulta verdadeira em todas as atribuições de valores de verdade às suas variáveis proposicionais (ver variável). (Desidério Murcho)
technê
Termo grego que refere o conhecimento técnico envolvido quando em práticas como a medicina ou o trabalho artesanal. Em algumas das suas obras, Platão defende que a filosofia é uma technê, no sentido de uma arte de viver virtuosamente. (Desidério Murcho)
teísmo
Concepção acerca da natureza de Deus que defende serem as seguintes as suas características ou atributos: é o único criador do universo, é omnipotente (pode fazer tudo), é omnisciente (sabe tudo), é livre e é infinitamente bom. Esta ideia de Deus está associada às grandes religiões monoteístas e a discussão acerca da existência de Deus tem sido, em grande parte, a discussão acerca da existência de um Deus com estas características. É o Deus teísta que está em causa quando, em filosofia, se discute o argumento ontológico, o argumento cosmológico, o argumento do desígnio, e o problema do mal. Ver também Deus e filosofia da religião. (Aires Almeida)
telos
Termo grego que significa “finalidade”. A noção era especialmente importante na filosofia de Aristóteles, que entendia que todas as coisas tinham uma finalidade natural. Este tipo de pensamento finalista é implausível em física, mas é mais adequado na biologia e na ética. (Desidério Murcho)
teoria
Um conjunto de proposições estruturadas entre si que visam resolver um problema ou explicar um fenómeno. Diz-se que são proposições estruturadas porque numa teoria as suas diferentes partes se articulam, isto é, apresentam uma estrutura lógica. As teorias não podem ser válidas ou inválidas no mesmo sentido em que um argumento é válido ou inválido; as teorias são verdadeiras ou falsas, tal como as proposições (e tal como as proposições podem ser fecundas ou estéreis, interessantes ou triviais, etc.). Não há uma receita automática para avaliar teorias, mas os seguintes aspectos devem ser tidos em conta: 1) Se o problema que uma teoria procura resolver é absurdo, a teoria é absurda; 2) Se uma teoria não resolve os problemas que se propunha resolver, ou não explica o que se propunha explicar, é inadequada; 3) Se uma teoria for inconsistente (ver consistência e inconsistência), é falsa; 3) Se uma teoria tiver consequências falsas, é falsa; 4) Se os argumentos que sustentam uma teoria forem maus, a teoria é má. (Desidério Murcho)
teoria das ideias
Platão refere em alguns dos seus diálogos (Fédon, Simpósio, República, etc.) a existência de entidades supra-sensíveis, a que dá o nome de “Ideias" (ou “Formas”), com a finalidade de explicar por que razão nos parece que quando estamos a referir objectos particulares como Sócrates, Einstein e Eusébio estamos, afinal, a falar da mesma coisa: homens. A razão é que todos eles exemplificam a Ideia ou Forma de Homem. Assim, dizemos que Sócrates, Einstein e Eusébio, são homens porque exemplificam, imitam ou participam da Ideia de Homem, ou de humanidade. As Ideias não são entidades mentais, mas extramentais e não são apreensíveis pelos sentidos; apenas pela razão. São também únicas (não há várias ideias de Homem, ou de Igualdade, Beleza, Justiça, etc.), perfeitas (não há exemplos perfeitos de coisas belas, mas a Ideia de Beleza é perfeita) e imutáveis (a beleza das coisas altera-se e é diferente de objecto para objecto, mas a Ideia de Beleza é inalterável). A Teoria das Ideias, apesar de ser uma teoria metafísica, tem importantes implicações epistemológicas. Ver também universais. (Aires Almeida)
teoria do gosto
Concepção estética que toma como problema central desta disciplina o problema do gosto. Para os filósofos do séc. XVIII, como Hume e Kant, os juízos estéticos como “esta música é bela” são subjectivos, sendo assim juízos de gosto. A caracterização e discussão dos juízos de gosto, nomeadamente os problemas de saber se os juízos de gosto são ou não universais (Kant) e se existe um padrão de gosto (Hume), passam a ocupar o centro das disputas acerca da estética. (Aires Almeida)
teoria dos mandamentos divinos
Teoria metaética segundo a qual os factos morais são instituídos por Deus. Quem subscreve esta perspectiva pensa, por exemplo, que mentir é errado unicamente porque Deus decretou ou estipulou que mentir é errado. Ockham conta-se entre os poucos filósofos que defenderam esta teoria. Tal como o relativismo moral, a teoria dos mandamentos divinos apresenta os factos éticos como simples convenções. Ver dilema de Êutifron. (Pedro Galvão)
terceiro excluído, princípio do
Ver princípio do terceiro excluído.
tese
Em geral, proposição ou doutrina apresentada para prova ou para consideração. Na filosofia de Kant, a tese é o primeiro termo da oposição dialéctica que constitui as antinomias (sendo o segundo a antítese), enquanto na de Hegel designa o primeiro termo de um sistema formado por tese, antítese e síntese, em que as duas primeiras se opõem uma à outra e a última as supera estabelecendo um ponto de vista superior, em que as outras se conciliam. (Álvaro Nunes)
tipos de argumentos
Ver argumentos, tipos de.
Tomás de Aquino (1225-74)
Um dos maiores filósofos do período medieval. Nasceu no seio de uma família aristocrata em Roccasecca em Itália. Estudou na escola dos monges beneditinos de Monte Cassino e na Universidade de Nápoles. Em 1244 juntou-se à Ordem dos dominicanos. Estudou em Paris e em Colónia com Alberto Magno. Sob a influência deste, tornou-se estudioso de Aristóteles e escreveu extensamente sobre a sua filosofia. As suas maiores obras são a Summa contra Gentiles (“Contra os Erros dos Infiéis”) e a Summa Theologiae (1266-73). Foi nesta última que expôs as suas famosas cinco vias ou argumentos a favor da existência de Deus. De todos, o mais conhecido é o argumento cosmológico, o qual é ainda bastante influente. Esta obra tornou-se um marco incontornável da filosofia medieval.
Uma das maiores preocupações de Tomás de Aquino consistiu em conciliar a doutrina cristã com o aristotelismo. Essa preocupação levou-o à defesa de uma teologia natural. Defendeu que algumas verdades religiosas são susceptíveis de ser descobertas e compreendidas pela razão, como é o caso da existência de Deus daí os seus argumentos a favor da existência de Deus. Contudo, achava que nem todas as verdades religiosas são susceptíveis de confirmação racional. No caso da doutrina da Trindade e da Incarnação, defendeu uma teologia revelada; ou seja, a verdade de tais doutrinas só pode ser conhecida através da revelação divina. A relação entre a fé e a razão tem um papel central na filosofia de Tomás de Aquino. Defendeu que tanto a fé como a razão são modos de chegar à verdade. Mas se a razão chegar a um resultado contrário à fé é porque cometemos um erro de raciocínio. A ideia é que a fé é uma forma infalível de chegar à verdade em questões religiosas. Tomás de Aquino preocupou-se ainda com questões éticas, epistemológicas e metafísicas. Em todas estas áreas tentou conciliar a doutrina cristã com o aristotelismo. Em 1323 foi canonizado pelo Papa João XXII que argumentou que apesar de Tomás de Aquino não ter feito milagres, cada problema filosófico a que respondeu representa um verdadeiro milagre. (Célia Teixeira)
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 8 (Lisboa: Temas e Debates, 1999).
Tomás de Aquino, O Ente e a Essência (Lisboa: Instituto Piaget, 2000).
tomismo
Corrente filosófica baseada nas ideias de Tomás de Aquino.
transcendental
Termo muito importante na filosofia de Kant, sobretudo na sua epistemologia. Significa “condição de possibilidade a priori de algo”. Refere-se na Crítica da Razão Pura a estruturas não empíricas que, contudo, se aplicam a objectos da experiência. Assim, a) espaço e tempo são formas a priori da sensibilidade que tornam possível a recepção dos dados empíricos; b) as categorias do entendimento são conceitos a priori que tornam possível o conhecimento científico dos dados recebidos pela sensibilidade; c) as ideias da razão (como a Ideia de Deus) são formas a priori que tornam possível não o conhecimento mas sim o progresso do conhecimento científico indicando ao entendimento um ideal: procurar explicações cada vez mais englobantes como se fosse possível atingir a explicação definitiva de todos os fenómenos. Transcendental distingue-se de transcendente porque, apesar de não ter origem empírica, está limitado à experiência. Transcendente é o que ultrapassa a nossa experiência possível, é a característica do que não pertence ao mundo natural. Deus é um ser transcendente mas a ideia de Deus é transcendental. (Luís Rodrigues)
transcendente
Ver imanente, transcendental.
U
Übermensch
Termo alemão usado por Nietzsche para designar o “sobre-humano”, “além-humano” ou “super-homem”: o ser que ultrapassa as limitações dos seres humanos, evoluindo para um estádio superior, livre de ilusões, nomeadamente as impostas pelas moralidades religiosas. (Desidério Murcho)
unidade da ciência
A ideia de unidade da ciência está associada a duas teses. Segundo uma delas, algumas ciências podem ser reduzidas a outras (por exemplo, a biologia à química), de tal maneira que em última análise todas as ciências podem, em princípio, ser reduzidas a uma única ciência englobante (geralmente a física). Há várias maneiras de entender a redução em causa (ver reducionismo). Pode-se sustentar, por exemplo, que as ciências são redutíveis à física no seguinte sentido: todas as afirmações de qualquer disciplina científica podem, em princípio, ser traduzidas para a linguagem da física (ver fisicismo). A outra tese associada à ideia de unidade da ciência diz-nos que todas as ciências obedecem essencialmente ao mesmo método e procuram fazer-nos perceber a realidade da mesma maneira. Os defensores desta tese costumam afirmar que há um modelo de explicação científica aplicável a todas as ciências. Alguns críticos desta perspectiva, como Wilhelm Dilthey (1833–1911), opõem a explicação à compreensão, sustentando que o recurso a esta última torna as ciências sociais muito diferentes das ciências da natureza. Quem, como os filósofos do positivismo lógico, advoga a unidade da ciência, costuma ter em mente apenas as ciências empíricas e, portanto, coloca a matemática e a lógica numa categoria distinta. Ver lei da natureza, método científico. (Pedro Galvão)
universais
Um universal é uma propriedade exemplificada por diferentes objectos (ou particulares). Por exemplo, quando digo “Sócrates é sábio”, a propriedade de ser sábio é exemplificada pelo particular Sócrates. Mas é também exemplificada por outros particulares: Platão, Gandhi, etc. Assim, o chamado “problema dos universais" consiste em saber se, além de particulares, como Sócrates e Platão, há coisas como a sabedoria, a brancura, a circularidade, etc. Os nominalistas afirmam que só há particulares e os realistas defendem que há universais. Mas se há universais, onde se localizam? Esta pergunta dá origem a diferentes tipos de realismo: transcendente e imanente. E será que há universais que não são exemplificados por particulares? Esta pergunta dá origem outros dois tipos de realismo: o platónico e o aristotélico. Os universais servem, alegadamente, para explicar a semelhança que se verifica entre objectos numericamente distintos. Há também diferentes tipos de nominalismo. (Aires Almeida)
universal afirmativa, proposição
Uma proposição com a forma “Todo o F é G”, como “Todos os homens são mortais”. A negação de uma universal afirmativa é uma particular negativa: “Alguns F não são G”. Assim, a negação de “Todos os homens são mortais” é “Alguns homens não são mortais”. Ver quadrado de oposição. (Desidério Murcho)
universal negativa, proposição
Uma proposição com a forma “Nenhum F é G”, como “Nenhum homem é eterno”. A negação de uma universal negativa é uma particular afirmativa: “Alguns F são G”. Assim, a negação de “Nenhum homem é eterno” é “Alguns homens são eternos”. Ver quadrado de oposição. (Desidério Murcho)
universal, proposição
Uma proposição dominada pelo quantificador “Todo”, como “Todos os homens são mortais”, “Nenhum homem é imortal”, etc. A negação de uma proposição universal é sempre uma particular. As proposições universais estão intimamente relacionadas com as condicionais (ver condicional); pode-se parafrasear qualquer universal dada numa condicional: a universal “Todos os homens são mortais” é equivalente à condicional “Se alguém é homem, é mortal”. (Desidério Murcho)
universal, quantificador
Ver quantificador universal.
universalizabilidade
Condição fundamental, segundo Kant, para que uma máxima possa ser moralmente aceitável (ver ética). Quando um agente moral faz algo por alguma razão, está a seguir uma máxima. Uma máxima é, pois, uma regra singular de acção que nos indica o motivo por que fazemos algo. Para Kant, a avaliação moral de um acto depende da máxima do agente. Uma máxima é moralmente aceitável se puder ser universalizada. Isto significa que deve poder valer para todos os seres racionais, transformando-se em princípio universal de conduta: “Todos devem agir assim”. (Luís Rodrigues)
uso e menção
Qual é a diferença entre “Beja é quente” e “"Beja" tem quatro letras"? No primeiro caso, estamos a usar a primeira palavra para referir a cidade alentejana; no segundo caso, estamos a mencionar a própria palavra “Beja”. No discurso escrito, o uso e a menção das palavras distingue-se pela utilização de aspas: se as palavras são usadas, não são escritas entre aspas; se são mencionadas, são escritas entre aspas. No discurso oral, só o contexto da elocução nos permite determinar se uma palavra está a ser usada ou mencionada. A distinção uso e menção é importante para evitar uma confusão entre as propriedades das coisas e as propriedades das palavras, como aconteceria ao dizermos que a palavra “Beja” é quente ou que a cidade alentejana tem quatro letras. (António Paulo Costa)
utilitarismo
Uma forma de ética consequencialista segundo a qual a nossa única obrigação fundamental é promover imparcialmente a felicidade ou o bem-estar, isto é, dar o mesmo peso aos interesses de todos os que serão afectados pela nossa conduta. Alguns utilitaristas, como Mill, defendem o hedonismo, mas outros, como Hare e Singer, concebem o bem-estar de um ser em termos da satisfação dos seus desejos ou preferências. Alguns utilitaristas defendem que temos de maximizar o bem-estar, isto é, promovê-lo tanto quanto possível. (Pedro Galvão)
utopia
Etimologicamente, o termo deriva das palavras gregas “ου" (não) e “τοπος" (lugar) e significa “que não está em nenhum lugar”. O seu uso tem origem na obra Utopia (1516) de Thomas More, em que uma sociedade concebida para a prática da virtude e a obtenção da felicidade, donde estão excluídos o dinheiro e a propriedade, é apresentada como a solução para o egoísmo da vida privada e pública da Europa de então. Contudo, já antes de More outros autores tinham apresentado utopias, sem usar esse nome: é o caso de A República (trad. 2001, Gulbenkian), de Platão. Uma utopia é uma descrição de um lugar ou de uma sociedade humana ideais e, a maior parte das vezes, constitui, ao mesmo tempo, uma crítica da sociedade do autor e uma sugestão de reformas sociais a implementar ou de objectivos a atingir. (Álvaro Nunes)
V
vagueza
Uma afirmação é vaga quando dá origem a casos de fronteira indecidíveis. Por exemplo, a frase “Sócrates era calvo” é vaga porque apesar de ser obviamente verdadeira caso Sócrates tenha zero cabelos, e falsa caso tenha muitos milhares, há casos intermédios em que não se sabe se a frase é verdadeira ou falsa. Toda a linguagem é vaga, mas devemos tentar ser tão pouco vagos e tão precisos quanto possível, particularmente em filosofia. Por exemplo, no dia-a-dia diz-se que o Fédon, de Platão, “tem a ver com” a imortalidade da alma, e que “remete para” problemas metafísicos. Mas em filosofia quer-se maior precisão: uma formulação e discussão clara dos problemas, teorias e argumentos discutidos e apresentados no Fédon. (Desidério Murcho)
validade formal e material
A validade formal e material é uma forma popular e confusa de falar de contradição e de verdade. Dizer que uma afirmação como “Os círculos são quadrados” não tem “validade formal” é apenas uma maneira confusa de dizer que essa afirmação é uma contradição (que não resulta, ironicamente, da sua forma lógica). E dizer que uma afirmação como “A neve é branca” tem “validade material” é apenas dizer que a afirmação é verdadeira. Em nenhum dos casos se trata realmente de validade e invalidade. Ver também a priori e a posteriori. (Desidério Murcho)
validade e invalidade
A correcção ou incorrecção de um argumento. Há dois tipos de validade: a dedutiva e a não dedutiva. Um argumento dedutivo é válido quando é impossível que as suas premissas sejam verdadeiras e a sua conclusão falsa; se isso for possível, o argumento é inválido. Um argumento não dedutivo é válido quando é improvável, mas não impossível, que as suas premissas sejam verdadeiras e a sua conclusão falsa; se for provável, é inválido. Não deve confundir-se este sentido lógico dos termos “validade” e “invalidade” com o seu sentido popular, que significa “com valor” e “sem valor”. Assim, popularmente diz-se que uma proposição é válida ou inválida, querendo dizer que tem valor ou que não tem valor (e, muitas vezes, que é verdadeira ou falsa). Mas não se pode dizer que uma proposição é válida ou inválida no sentido lógico do termo. No sentido lógico do termo só os argumentos podem ser válidos ou inválidos; as proposições são verdadeiras ou falsas, interessantes ou entediantes, e muitas outras coisas, mas nunca podem ter a propriedade da validade argumentativa. Ver verdade. (Desidério Murcho)
valor
Quando reconhecemos um valor nas coisas (por exemplo, considerando-as belas, justas ou sagradas), inclinamo-nos a ter uma atitude favorável para com elas que se reflecte nos nossos actos e escolhas (ver acção). Quem tem uma postura objectivista em relação aos valores julga que as coisas são valiosas independentemente de as valorizarmos, mas para um subjectivista as coisas são valiosas simplesmente porque as valorizamos. Atribuir valor instrumental a uma coisa é considerá-la valiosa apenas em virtude de esta ser um meio para alcançar aquilo que julgamos ter valor em si — isto é, aquilo que julgamos ter valor intrínseco. Ver hedonismo, objectivismo e subjectivismo, juízo de facto e juízo de valor. (Pedro Galvão)
valor de verdade
Ver verdade, valor de.
variável
Em lógica, um símbolo usado para representar um objecto ou uma proposição. No cálculo proposicional as letras P, Q, etc. são normalmente usadas como variáveis proposicionais para representar qualquer proposição. Por exemplo, a expressão “Se P, então Q” permite representar a afirmação “Se está a chover, não vou à praia”, representando P “Está a chover” e Q “Não vou à praia”. No cálculo de predicados as letras x, y, etc., são normalmente usadas como variáveis predicativas para representar qualquer objecto de um conjunto especificado de objectos. Por exemplo, dado o conjunto dos seres humanos, o símbolo x pode ser usado em “x é mortal”, para representar qualquer um de nós. Ver lógica e símbolos lógicos. (Célia Teixeira)
verdade lógica
Ver tautologia.
verdade, condições de
Ver tabela de verdade.
verdade, tabela de
Ver tabela de verdade.
verdade, valor de
O valor de verdade de uma proposição é o facto de essa proposição ser verdadeira ou falsa. Por exemplo, o valor de verdade de “A neve é branca” é “verdadeiro”, e o valor de verdade de “A neve é azul” é “falso”. Alguns filósofos defendem que há outros valores de verdade; outros que nem todas as proposições têm valor de verdade. Do ponto de vista estritamente lógico pode-se ter os valores de verdade que se quiser; a dificuldade é saber se estamos apenas a inventar ficções ou a falar de valores de verdade reais. (Desidério Murcho)
verdade e falsidade
A verdade e a falsidade são propriedades de afirmações ou de proposições, e não de argumentos, conceitos ou coisas extralinguísticas. Os argumentos não podem ser verdadeiros nem falsos, mas são válidos ou inválidos (ver validade e invalidade); por exemplo: o modus tollens não pode ser verdadeiro nem falso. Os conceitos não podem ser verdadeiros nem falsos, mas têm extensão ou não; por exemplo, o conceito homem imortal não tem extensão porque não há homens imortais. E as coisas extra-linguísticas não podem ser verdadeiras nem falsas (excepto metaforicamente), mas são reais ou não; por exemplo: uma laranja ou uma obra de arte não podem ser verdadeiras nem falsas. Uma afirmação como “A neve é branca” é verdadeira se, e só se, a neve é branca; e é falsa se a neve não for branca. Esta é a noção central de verdade e falsidade, que por vezes se exprime assim: Uma afirmação “P” é verdadeira se, e só se, P. Há várias teorias que tentam desenvolver esta noção central de verdade, nomeadamente teorias da verdade como coerência, correspondência, descitação, etc. (Desidério Murcho)
verificabilidade
Diz-se de uma afirmação que é verificável. Por exemplo, a frase “Há relva verde” é verificável, pois podemos observar a relva para ver se a frase é ou não verdadeira. Já a frase “As ideias incolores verdes dormem furiosamente juntas” não é verificável, pois nada há que possamos observar de modo a podermos ver se é ou não verdadeira. Este princípio só se aplica a frases sintéticas (ver analítico e sintético). Os positivistas lógicos (ver positivismo lógico) defendiam que as frases que não são verificáveis nem analíticas não têm sentido. Ver verificacionismo. (Célia Teixeira)
verificacionismo
Tese central do positivismo lógico segundo a qual o significado de uma frase é o seu método de verificação. Esta tese foi usada pelos positivistas nos seus ataques à metafísica. Para eles, as frases de natureza metafísica não eram verificáveis, e como tal a metafísica devia ser abandonada. Por “verificação” entende-se em geral “verificação empírica”, de modo que este princípio apenas se aplica a frases sintéticas (ver analítico e sintético). Dado que para os positivistas as frases analíticas não tinham conteúdo factual, isto é, não eram acerca do mundo, esta tese não se lhes aplicava. Quine foi um dos maiores opositores do verificacionismo, defendendo que as frases não podem ser verificadas isoladamente; têm de o ser em conjunto (ver holismo). Ver Carnap, Wittgenstein. (Célia Teixeira)
verificável
Ver verificabilidade.
vida, sentido da
Ver sentido da vida.
virtude
Ver ética das virtudes.
vontade
O poder de desejar um certo resultado. Muitos filósofos distinguiram a vontade do simples apetite ou inclinação, reservando para aquela um estatuto mais elevado por depender da capacidade de antecipar resultados, que por sua vez depende do raciocínio. Jean-Jacques Rousseau (1712–78), no seu livro O Contrato Social (1762, trad. 1981, Europa-América) defendeu que a vontade geral é a vontade da sociedade civil concretizada nas instituições políticas. Para Kant, a vontade boa é aquela que, lutando contra os desejos e inclinações egoístas, determina a acção de acordo com o imperativo moral, e a vontade santa é aquela que o faria espontaneamente e sem tal luta. Para Nietzsche, a vontade de poder é a característica fundamental da natureza humana. Ver razão, desejo e intenção. (António Paulo Costa)
vontade boa
Designa, em Kant, a vontade que respeita a lei moral por si mesma, considerando imperativo cumprir o dever incondicionalmente. Qualquer outro sentimento, qualquer cálculo interessado ou outras inclinações sensíveis retiram todo o valor moral às decisões e acções da vontade, tornando-a dependente de algo exterior, ou seja, heterónoma. Obedecendo unicamente às exigências da razão (a lei moral é uma lei puramente racional) a vontade boa é a vontade autónoma. (Luís Rodrigues)
W
Weltanschauung
Termo alemão que significa “concepção geral do mundo”.
Wittgenstein, Ludwig (1889–1951)
Filósofo austríaco. Wittgenstein nasceu em Viena e estudou filosofia, em Cambridge, sob a orientação de Russell. Enquanto prisioneiro de guerra terminou, em 1919, o manuscrito do seu Tractatus Logico-Philosophicus, com o qual pensava ter resolvido todos os problemas filosóficos genuínos. Depois de um interregno, em que foi professor primário e jardineiro, regressou à Universidade de Cambridge em 1929. Durante a Segunda Guerra Mundial chegou a trabalhar como porteiro, mas em 1945 voltou a dar aulas em Cambridge. Desagradado com a vida académica, demitiu-se em 1947. Morreu de cancro em 1951. O contributo de Wittgenstein para a filosofia costuma, por facilidade, dividir-se em dois períodos, identificados pelas suas duas mais representativas obras (o Tractatus, publicado em 1921 e as Investigações Filosóficas, publicadas postumamente em 1953; ambos trad. 1995, Gulbenkian). Na primeira expõe a sua teoria pictórica da linguagem, segundo a qual as proposições expressas em frases com significado são como representações pictóricas dos factos a que se referem (na medida em que se deixam analisar em elementos básicos que correspondem aos indivíduos e às relações entre indivíduos que constituem esses factos). Para além de proposições com conteúdo factual determinado e tautologias, nada pode dar origem a frases com sentido (as afirmações éticas, estéticas e a esmagadora maioria das teses defendidas pelos filósofos ao longo da história, em particular metafísicas, são assim desqualificadas como destituídas de sentido — uma concepção adoptada pelos positivistas lógicos). Na segunda fase da sua vida filosófica, Wittgenstein adoptou um ponto de vista diferente acerca da linguagem e do tipo de deficiências que a podem afectar. Preocupou-se, em particular, com a relação entre a linguagem e as intenções com as quais a usamos em contextos particulares, praticando assim alguma acção (por exemplo, pedir, perguntar, ordenar, informar, etc.). A cada tipo de acção (e de intenção associada) corresponde um “jogo de linguagem" com regras próprias, cuja infracção leva à produção de sequências linguísticas sem sentido (de modo que aquilo que Wittgenstein considerava ser a esterilidade da filosofia tradicional é agora visto como o resultado deste tipo de infracção). O ponto comum às duas fases da filosofia de Wittgenstein é a preocupação com os limites da linguagem e com as pseudo-afirmações, pseudo-argumentos e pseudo-teses que o desrespeito desses limites pode gerar. A sua concepção da filosofia como disciplina essencialmente terapêutica, cujo objectivo é apenas curar-nos das “enfermidades" conceptuais resultantes desse desrespeito, manteve-se constante. A visão catastrófica de Wittgenstein acerca dos problemas filosóficos tradicionais deixou de ter aceitação, mas a sua influência (sobretudo na filosofia analítica) no modo como os filósofos se precavêem contra o uso incorrecto, impreciso ou superficial da linguagem perdurou até hoje. Por outro lado, as suas tendências místicas e o seu versátil conceito de “jogo de linguagem" influenciam ainda hoje algumas correntes filosóficas e, em alguma medida, as ciências humanas (o referido conceito inspira frequentemente teorias relativistas — ver relativismo). Wittgenstein produziu ainda contributos importantes em filosofia da matemática e em filosofia da mente, e a sua ênfase na relação entre linguagem e acção foi uma influência decisiva no desenvolvimento da pragmática. Além do Tractatus e das Investigações, outras obras importantes de Wittgenstein são Remarks on the Foundations of Mathematics (1956) e O Livro Azul (1958; trad. 1992, Edições 70) e O Livro Castanho (1958; trad. 1992, Edições 70). Ver também filosofia da linguagem. (Pedro Santos)
Kenny, Anthony, História Concisa da Filosofia Ocidental, cap. 22 (Lisboa: Temas e Debates, 1999).
Magee, Bryan, Os Grandes Filósofos, cap. 15 (Lisboa: Presença, 1989).
X
Xenófanes de Colofonte (c. 570–c. 475 a. C.)
Filósofo pré-socrático, poeta e rapsodo, considerado por Platão e Aristóteles o fundador da escola eleática, por ter antecipado os pontos de vista de Parménides. Criticou o antropomorfismo e o imoralismo dos deuses em Homero e Hesíodo, apontando no sentido de um Deus único, espiritual e transcendente, que foi o primeiro a defender por meios estritamente racionais. Também afirmou que não é possível conhecer a verdade e que todo o conhecimento é conjectural. Dos seus escritos apenas chegaram até nós pequenos fragmentos. (Álvaro Nunes)
Z
Zenão de Cítio (334-262 a. C.)
Filósofo grego que fundou em Atenas, cerca de 300 a. C., a escola estóica (ver estoicismo) — de Stoa Poikilê (pórtico pintado), o nome do local onde dava as suas lições. Foi discípulo dos filósofos cínicos Crato de Tebas e Estílpone de Mégara e do filósofo platónico Xenócrates. Todos os seus escritos se perderam, mas sabe-se que escreveu uma obra, intitulada República, em que defendeu a importância da lei e a universalidade das instituições políticas. Defendeu também uma concepção absoluta do dever moral e que a felicidade consiste na conformidade da nossa vontade à razão divina que governa o universo. O estoicismo, que além da ética incluía a lógica, a teoria do conhecimento e a física, constituiu a escola filosófica mais importante do período helenístico. (Álvaro Nunes)
Zenão de Eleia (n. c. 490 a. C.)
Filósofo grego, discípulo de Parménides. Escreveu um livro, do qual se conhecem apenas fragmentos, a defender as ideias do seu mestre de que o movimento e a pluralidade não passam de ilusões (ver ilusão). Os seus quatro argumentos contra a realidade do movimento, conhecidos como “paradoxos de Zenão”, sobretudo o paradoxo da corrida entre Aquiles e a tartaruga, tornaram-no muito famoso. (Aires Almeida)
Zeitgeist
Termo alemão que significa “espírito do tempo”, isto é, a mentalidade de uma dada época. (Desidério Murcho)
ISSN 1749-8457