Ver superfícies e objectos físicos

Não poucos filósofos de admirável inteligência consideraram que o facto de normalmente não conseguimos ver de um objecto físico mais do que uma parte da sua superfície tem consequências paradoxais, ou seja, que dele decorre que a crença de “senso comum” segundo a qual podemos ver objectos físicos e, com base nisso, saber que há tais objectos tem de ser ou decididamente rejeitada ou substancialmente modificada.¹ A reacção crítica normal a essa perspectiva tem sido a de que, pelo contrário, ver um objecto físico simplesmente é (em termos triviais) ver uma parte da sua superfície. Segundo os críticos,² alguns filósofos deixaram-se impressionar excessivamente por um facto trivial, em virtude de pressuporem que faz parte do significado de “ver” esta palavra se aplicar a A somente se sucede de aplicar-se a toda e qualquer parcela de A.

Será que esses críticos têm razão? Terá sido por fazerem tal pressuposição que os filósofos foram levados a pensar que o facto de normalmente não podermos ver de um objecto físico senão parte da sua superfície (ao qual me referirei, em prol da concisão, como “facto-Q”, sendo “Q” uma forma de abreviar “quanto”) não é trivial mas que tem importantes e surpreendentes consequências epistemológicas? Será, na verdade, o alegado facto-Q realmente trivial?

I

Como sustentam tal conclusão os filósofos que consideram não ser trivial o facto-Q? É interessante que não apresentem argumento algum a seu favor. Pelo contrário, falam como se nos bastasse constatar que não podemos ver o lado oposto ou o interior, mas apenas parte da superfície do objecto diante de nós, para então vermos imediatamente que a nossa posição não é tão boa quanto supunha o senso comum. Falam como se chegar à conclusão a que chegam fosse como repararmos subitamente em um ruído no motor, que antes nos passara despercebido, o que nos despertaria imediatamente da nossa falsa complacência. Porém, dificilmente resistimos a rejeitar sem mais considerações esta sugestão, pois poderá algo ser mais absurdo do que supor que tenha passado despercebido a gerações de pessoas simples o facto de normalmente não podermos ver senão uma parte da superfície de um objecto físico? Logo, dificilmente se evita a ideia de que alguma(s) premissa(s) não explícitas devem ter levado o filósofo a pensar que o facto-Q tem consequências paradoxais.

Não obstante, jamais faremos jus à posição do filósofo se, ao rejeitar a descrição que o próprio nos dá de como chega às suas conclusões paradoxais, nos pormos em busca de pressuposições que imaginamos que ele deve ter feito. Haveria obviamente uma verdade importante na sua própria descrição, tivesse o filósofo argumentado como faz P aqui:

Consideremos uma situação em que outra pessoa X observa um objecto físico, digamos, um tomate, em condições normais (representadas pelo diagrama VT; sendo “VT ” uma abreviação para “Ver o Tomate”). Talvez esteja sentada à secretária no seu gabinete e o tomate esteja à sua frente, sobre a dita secretária. É este o tipo de situação em que diríamos que outra pessoa, X, pode ver um tomate.

Porém, quanto do tomate pode X ver? Não pode ver porção alguma do lado oposto ou do interior. Assinalemos este facto no diagrama, indicando as marcações cruzadas a porção do objecto físico que X não pode ver. (Em condições ideais, digamos, em uma palestra, usando um quadro negro, começaríamos por VT, aí assinalando em seguida esses factos. Aqui, contudo, temos de os assinalar em um diagrama separado, VTa, que é o mesmo que VT, excepto as marcações. A letra “a” em “VTa ” é uma abreviação para “assinalado”. As marcações cruzadas na metade do tomate orientada para X indicam que toda esta metade, excepto a superfície do hemisfério orientada para X, não é vista por X. ) Do objecto físico, X não consegue senão ver uma porção da superfície orientada para si. Indiquemos esse facto mais explicitamente no diagrama, marcando a negro a porção de superfície que ele consegue ver.

Como nos parecem as coisas, agora que assinalámos esses factos no diagrama?

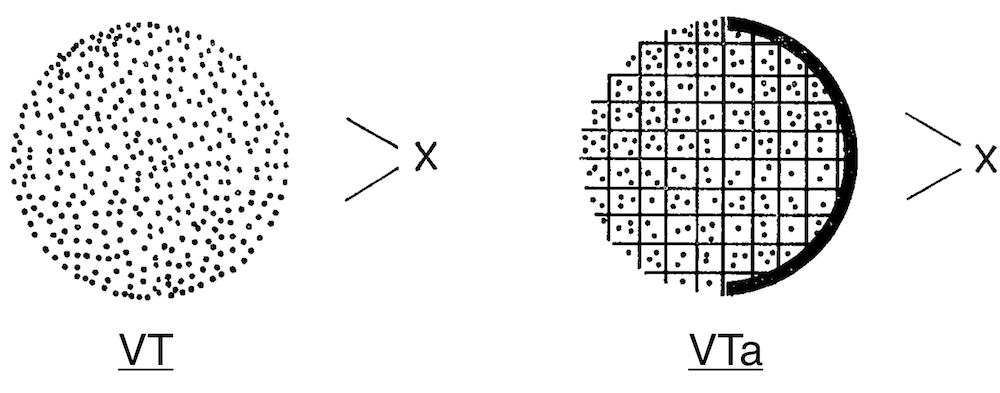
(Evidentemente, estamos a considerar agora VTa. ) Afirmámos ser este o tipo de situação em que diríamos que X pode ver o tomate. Mas será que pode? Não, não pode. Como é óbvio, tudo o que ele pode realmente ver é aquela porção da superfície orientada para si, indicada pela linha preta. Podemos assim ver que nos enganámos ao supor que X podia realmente ver o próprio objecto físico.

A apresentação que P nos dá das suas razões revela como puderam os filósofos vir a pensar que tendo nós (meramente) constatado o facto-Q vemos que não estamos perceptualmente em uma tão boa posição como imaginávamos. Quando passamos de VT para VTa parece, como afirma P, que simplesmente nos apercebemos ou que assinalámos o facto de que X não pode ver do objecto físico senão parte da sua superfície. No entanto, quando passamos para VTa, a posição de X subitamente parece mesmo pior. O quebra-cabeças não é sobre como P poderia ter suposto que uma vez tendo (meramente) constatado o facto-Q veria que a posição de X é pior do que ele ou nós, como pessoas simples, teríamos suposto — pois isto é precisamente o que parece suceder — mas antes sobre como pode não ser isto o que realmente sucede. A haver um truque mental aqui, qual é?

II

Embora possa considerar suficientemente óbvio que a posição perceptual de X não parece pior quando passamos para VTa, procurarei de seguida esclarecer ainda mais isto, ou antes, firmar uma asserção mais forte acerca do funcionamento da apresentação de P, pois afirmar que a posição perceptual de X em VTa parece, mas que apenas parece, pior do que a posição em que comummente supomos que ele pode estar em uma situação como VT é um eufemismo. A posição de X em VTa não é tão boa quanto a posição em que comummente supomos que ele pode estar. O ponto forte mais saliente na posição de P é o seguinte: depois de (aparentemente apenas) “constatarmos” o facto-Q vemos de facto que a posição perceptual de X não é tão boa quanto aquela em que pensávamos que ele se encontrava antes de “constatarmos” este facto. Logo, a haver algum truque mental na apresentação de P, residirá no “constatar”. Pois se o que fazemos consiste apenas em constatar o facto-Q então aprendemos genuinamente, como defende P, que a posição perceptual de X não pode ser tão boa quanto supõe o senso comum. Descobrimos genuinamente que o facto-Q tem esta consequência paradoxal, a menos que este “constatar” não seja genuíno, mas na verdade um ato que modifica a posição de X e o põe numa situação pior do que aquela em que se encontrava em VT. Se este “constatar” for espúrio nesse sentido, o que descobrimos é que a lógica de “ver” é tal que um certo ato que parece consistir apenas em constatar um facto pode, na verdade, piorar a posição perceptual de X.

Em suma, a apresentação de P é caracterizada pelas seguintes duas proposições:

• I. Fazemos o que parece apenas constatar um facto (o facto-Q) acerca do tipo de situação em que comummente supomos que outra pessoa pode ver um objecto físico.
• II. Após “constatar” este facto-Q, vemos que a posição perceptual em que X se encontra é inferior à posição em que considerávamos que ele se encontrava antes de “constatarmos” este facto.

A proposição (II) é deliberadamente ambígua. Afirma que em VTa a posição perceptual de X é pior do que a posição em que suporíamos que X estava em VT, mas deixa em aberto se “constatar” o facto-Q é um constatar genuíno, e portanto apenas uma parte de chegar a ver que a posição de X em VT é pior do que supúnhamos, ou se este “constatar” é espúrio, fazendo que a posição de X seja pior do que a sua posição anterior em VT. Se o “constatar” é genuíno, VTa revela o verdadeiro estado de coisas em VT. Se não é genuíno, VT e VTa são situações essencialmente diferentes.

Conjuntamente, (I) e (II) afirmam que P é levado à sua posição não pelo raciocínio nem pela argumentação, mas por fazer algo, por executar um ato, que parece apenas uma parte inocente de averiguar os factos acerca de uma situação. Faríamos bem, portanto, em não falar dos “argumentos” ou mesmo das “considerações” que levaram P à sua posição, mas antes, como farei, da aparentemente inocente “averiguação” que a isso conduz. Uma vez que esta averiguação se centra em ver parte da superfície de um objecto físico, referir-me-ei à mesma, em prol da concisão, como a “averiguação de superfície”.

Vejamos agora mais cuidadosamente se (II) se aplica ou não à averiguação de superfície levada a cabo por P. Temos também de ver ao certo de que maneira a posição perceptual de X em VTa é inferior à posição em que comummente supomos que ele se encontra em VT. Terá P razão? Isto é, será verdade em VTa que X não pode ver o tomate, que tudo o que pode realmente ver é parte da sua superfície?

É curioso, além de importante, que embora todo o filósofo que considera que o facto-Q tem uma consequência paradoxal pense que isso significa que, de algum modo, a crença de senso comum em como podemos ver objectos físicos está errada, não há entre tais filósofos acordo acerca de como, exactamente, essa crença está errada. Claramente Descartes, a partir do que afirma no seu exemplo dos “chapéus e capas”,³ consideraria que do facto-Q decorre que não podemos ver objectos físicos. Moore considera que dele decorre que “sempre que falamos, de maneira aproximada, em ver um qualquer objecto, é verdade que, em outro sentido mais estrito da palavra ver, apenas vemos uma parte do mesmo.”⁴ Broad defende que o que descobrimos é que “a situação perceptual inclui como constituinte” não o próprio objecto físico, como, de acordo com Broad, sugere o discurso de senso comum, mas, quando muito, apenas parte da superfície do objecto físico.⁵ A questão que gera esta controvérsia, expressa nos termos da averiguação de superfície de P, é a seguinte: “Podemos dizer de X que em VTa ele vê o tomate?” O facto de uma questão gerar essa controvérsia sem fim sugere que pode haver algo de errado na própria questão e argumentarei mais tarde que, na verdade, tal questão não é tão pacífica quanto esses filósofos supõem. Todavia, pretendo agora argumentar que que cada um destes vários filósofos tem razão em um aspecto, nomeadamente, que seja qual for ao certo a posição perceptual de X em VTa, ela não é tão boa quanto a posição em que suporíamos que ele se encontrava em VT. Para mostrar que assim é, procurarei agora tornar claro que ainda que de X se possa dizer que vê o tomate em VTa, o seu ver este objecto físico em VTa não é “tão bom quanto” supomos que pode ser numa situação como VT.

Considere o leitor qualquer objecto físico observável na sua proximidade, digamos, uma caneta. Agora imagine que uma fina porção da caneta (uma porção que inclui aquela parte da superfície orientada para si que pode ver, mas que também tem alguma espessura) se destaca da mesma e desloca ligeiramente na sua direcção e que esta porção obscurece completamente o resto da caneta. Que efeito tem isto no que o leitor, como pessoa simples — isto é, pondo de lado quaisquer convicções filosóficas que possa ter acerca de percepção —, diria que vê? Bom, sem dúvida diria que agora vê somente a porção destacada, não? Antes de a porção se destacar dizemos “vejo uma caneta”. Depois de estar destacada e deslocada para a frente dizemos “agora vejo apenas uma fina porção de uma caneta”.

Considere agora as seguintes figuras:

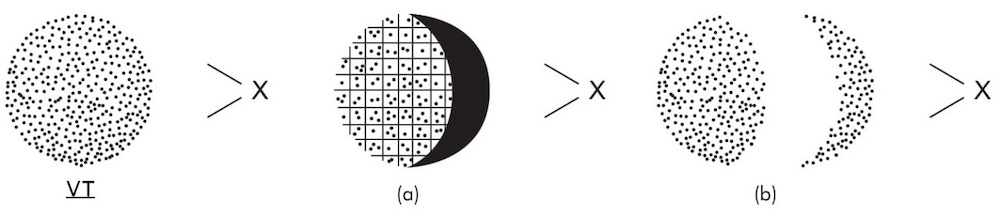
A figura à esquerda é, uma vez mais, VT. A fig. (a) é como VTa excepto que em (a) “assinalámos” no diagrama não o facto-Q propriamente dito mas o facto de que X não pode ver do tomate senão a sua quarta parte direita (sem com isso querer dizer, evidentemente, que ele pode ver sequer este tanto do tomate). Em (b) esta quarta parte direita está destacada e deslocada ligeiramente na direcção de X; oculta-lhe o resto do tomate. Se nós (como pessoas simples) começarmos por dizer em VT “Aqui X pode ver o tomate”, então quando passamos a (b) diríamos, no mesmo sentido, “Aqui X pode ver apenas a quarta parte direita do tomate”. Suponhamos, todavia, que começamos por (a) em vez de VT, dizendo de (a) “Aqui X pode ver o tomate”. O que, se dizemos isto, será então natural dizer no mesmo sentido quando passamos para (b)? Talvez não seja natural dizer coisa alguma. Seguramente, não deveríamos dizer: “Aqui X pode ver apenas a quarta parte direita”! No que diz respeito a apenas a quarta parte direita do tomate ser vista em (a) isso está, por assim dizer, “em paridade” com a quarta parte direita em (b), ao passo que em VT é o próprio tomate que parece estar em paridade com a quarta parte direita em (b). A posição perceptual produzida ao se cortar o tomate é consideravelmente pior do que a posição em que X parece estar em VT, mas mal difere (se é que, na verdade, difere em algo) da posição em que X se encontra após o “assinalamento”, isto é, em (a).

Evidentemente, o que se aplica ao “assinalar” do facto de que X não pode ver do objecto físico senão a sua quarta parte direita aplica-se também ao “assinalar” do próprio facto-Q.⁶ Ainda que se possa dizer de X que vê o objecto físico em VTa, o seu ver este objecto não é tão bom como parece em VTa, o seu ver este objecto não é tão bom como parece em VT. De que maneira, ao certo, é inferior, não é fácil especificar. Poderíamos dizer que, em VTa, X não pode ver o tomate “da maneira” como pode vê-lo em VT (não “directamente”, apenas “indirectamente”), ou que em VTa o tomate não tem bem o “estatuto” de ser visto que parece ter em VT. Não há que nos preocuparmos em demasia, porém, com o facto de que, ao tentar caracterizar a inferioridade a que o ver de X em VTa está sujeito, somos aparentemente forçados a usar distinções ou modos de expressão que, pelo menos neste caso, parecem duvidosos, pois estas dificuldades poderão muito bem dever-se ao facto de que, como irei sugerir mais tarde, ao conceder a verdade de que, em VTa, X pode ver o tomate, concedemos demasiado.

Concluo que a averiguação de superfície de P é apropriadamente descrita por (I) e (II) (reformuladas abaixo).

• I. Fazemos o que parece apenas constatar um facto (o facto-Q) acerca do tipo de situação em que comummente supomos que outra pessoa pode ver um objecto físico.
• II. Após “constatar” este facto-Q, vemos que a posição perceptual em que X se encontra é inferior à posição em que considerávamos que se encontrava antes de termos “constatado” este facto.

Como é óbvio, quando pensa que o facto-Q tem consequências paradoxais, o filósofo (Descartes, Moore, Broad, entre outros) está considerando o que ele pode ver, e não, como P, o que diria que outra pessoa pode ver. Tal diferença, porém, não tem quaisquer consequências neste caso, como cada um de nós pode verificar por si mesmo. Evidentemente, para “constatar” o facto-Q não assinalamos literalmente um diagrama ou objecto, mas podemos “assinalar” mentalmente o facto-Q no objecto diante de nós, por exemplo, imaginando marcas cruzadas sobre as porções do objecto que não podemos ver. Alternativamente, este “constatar” pode ser apropriadamente realizado imaginando um plano geométrico (bidimensional) inserido no objecto físico diante de nós, entre a porção proximal da sua superfície e o resto do objecto; ou podemos apenas, de uma qualquer maneira que pareça natural, tomar (“separar mentalmente”) esta porção da superfície ao resto do objecto. Quando fazemos qualquer uma destas coisas, parece mesmo que apenas constatamos o facto de que não podemos ver do objecto físico diante de nós senão a porção proximal da sua superfície, e, no entanto, este “constatar” tem exactamente as mesmas consequências para a nossa posição perceptual que o “assinalamento” teve para a posição de X. A única razão pela qual trabalhei aqui com a versão de P da averiguação de superfície é que me permitiu realizar aquele ato exigido de “constatar” publicamente, que, na versão mais fundamental, cada um de nós tem de realizar “na sua cabeça”.

III

Vimos que a menos que o “constatar” do facto-Q seja espúrio, redundando, na verdade, em um ato que, ao ser realizado, gera uma posição perceptual diferente, pior, a averiguação de superfície é válida, isto é, descobrimos realmente que em virtude de não podermos ver de um objecto físico senão parte da sua superfície, a nossa posição perceptual é pior do que, com optimismo, havíamos suposto. É um erro pensar que os filósofos consideraram o senso comum erróneo em virtude de suporem que parte do significado de “ver” está em que a palavra se aplica a A apenas quando se aplica a toda e qualquer porção de A. Este “pressuposto”, ou alguma versão aproximada do mesmo, verifica-se, de facto, em VTa. Aí, com efeito, é verdade que, em virtude de X não poder ver do objecto físico senão parte da sua superfície, não se pode dele dizer que vê este objecto “do modo” como parece que pode fazê-lo em VT (se é que, na verdade, se pode dizer que vê de todo o objecto). Não nos é dado compreender o filósofo se tomarmos este “pressuposto” como a base da sua perspectiva, pois fazer isso é tratar uma conclusão como se fosse uma premissa. É como supor que Zenão pressupõe tacitamente que não podemos percorrer uma distância finita e que as suas conclusões se desmoronam uma vez que se traga à luz este “pressuposto”. A única maneira de mostrar que o filósofo está errado é mostrar que o “constatar” do facto-Q envolve um truque, que na verdade produz uma situação perceptual diferente, mais pobre.

Como poderia esse “constatar” ser vicioso? A verdade, creio, está em que o culpado aqui é o “facto-Q”, pois não se trata realmente de um facto, e que o “constatar” é comparativamente inocente, pois “constatar” esse “facto” é ver o que seja ser verdade que não podemos ver de um objecto físico mais do que parte da sua superfície.

Para explicar isto, tenho de discutir certas propriedades particulares do conceito “ver”. Convém, todavia, considerar primeiro um conceito trivial, “estar mordiscado”⁷ , acerca do qual não temos quaisquer convicções, preconcepções ou preconceitos filosóficos. Demorar-me-ei um pouco, receio, neste conceito nada excitante, mas espero que com isto esclareçamos a natureza da percepção.

Podemos começar a nossa análise de “estar mordiscado” considerando os seguintes exemplos. A Fig. (1) abaixo representa um pedaço de queijo que está mordiscado (como se indica).

Com referência a (2), que representa o mesmo pedaço de queijo, é dito o seguinte: “Considere a metade do queijo marcada com linhas verticais e a metade⁸ marcada com linhas horizontais. Agora, quanto do pedaço de queijo está mordiscado? É natural responder: “Apenas a metade direita”. Na Fig. (3) há que considerar as secções marcadas com linhas verticais e horizontais. Se, acerca de (3), nos perguntassem “Quanto do pedaço de queijo está mordiscado?” responderíamos naturalmente “Apenas a quarta parte na extremidade direita”. É claro, a partir de (2) e (3), que os factores físicos não determinam por si sós quanto do pedaço de queijo está mordiscado. A quantidade que se diz ter sido mordiscada depende, evidentemente, de factores físicos, mas não exclusivamente desses factores; depende também de que porções do pedaço de queijo são tomadas como porções unitárias. É patentemente verdade, por assim dizer, em vez de apenas ser verdade em uma qualquer maneira de dizer, que em (2) metade do queijo está mordiscada. Não há em (2) uma porção do pedaço de queijo que, independentemente de qualquer especificação de porções unitárias relevantes, seja a porção realmente mordiscada. Em suma, não é um facto físico que uma certa porção de A está mordiscada.

Por outro lado, o facto de que uma certa porção do queijo foi mordiscada ⁹ é um facto físico. É também um facto físico que, por exemplo, em (2) a maior parte da metade direita do queijo não está mordiscada, mas, apesar deste facto físico, a metade direita ela mesma está mordiscada.

Em contextos onde não há indicação sobre que porções de A devem ser tomadas como unidades relevantes, não há tal coisa como uma porção de A que está mordiscada. Tal não significa, evidentemente, que nessas situações nenhuma parte de A está mordiscada, mas antes que em tais contextos a questão “Quanto de A está mordiscado” não tem resposta. O caso (1) (p. 106) ilustra isto. Imagine que em referência a (1) nos perguntam: “Quanto deste pedaço de queijo está mordiscado? A quarta parte direita? A metade direita? Ou...” O que havemos de responder? A única maneira de responder a esta pergunta é rejeitá-la. Para dizer quanto está mordiscado teríamos primeiro de designar algumas porções como unidades relevantes e não temos aqui base alguma para fazer uma escolha. É como se nos apresentassem uma série de bolas de borracha, todas igualmente em bom estado, e, sem que nos fosse dito algo mais excepto que nada mais há para dizer, nos perguntassem “Qual deveríamos escolher?” Não há, neste contexto, tal coisa como uma bola que deveria ser escolhida.

Em seguida, consideremos o que dizer acerca de A ele mesmo ter sido mordiscado em contextos em que há tal coisa como uma quantidade de A que está mordiscada.

Suponhamos que nos perguntam, na situação (2) (p. 106) “Está o pedaço de queijo mordiscado?” À partida, esta pergunta pode parecer bastante directa. Mas em vez de responder pela afirmativa, alguém poderia replicar: “Não, o pedaço de queijo não está mordiscado. Tudo o que na verdade está mordiscado é a metade direita.” O que dizer acerca desta resposta? Está errada? É ininteligível? Nenhuma destas. Experimente afirmá-lo. Quando o fazemos, parece haver algo em tal resposta. Na verdade, enquanto a damos, a resposta parece verdadeira. Pelo que essa resposta negativa à pergunta não pode simplesmente ser rejeitada como errada ou ininteligível. Não é claro o que, ao certo, deveríamos dizer acerca da mesma.

Além disso, simplesmente afirmar “Em (2) o pedaço de queijo está mordiscado” deixa por dizer algo importante. O próprio pedaço de queijo, de algum modo, não está em (2) tão bem no que diz respeito a ter sido mordiscado como está em (1). Talvez pudéssemos exprimir esta diferença dizendo que em (2) o “estatuto” do queijo, de estar mordiscado, não é tão bom quanto o “estatuto” de estar mordiscado, de que goza em (1). Em (2) somente a sua metade direita está, no que diz respeito a ser mordiscada, “em paridade” com o pedaço de queijo ele mesmo em (1). Reconhecemos esta diferença nas nossas respostas a certas perguntas. Suponhamos que nos perguntam, com referência a (1) “Em que consiste o pedaço de queijo estar mordiscado?” Deveríamos naturalmente responder do seguinte modo: “Consiste em um animal ou humano ter removido à dentada porções irregulares deste pedaço de queijo”. Ou seja, respondemos a esta pergunta afirmando, ou procurando afirmar, o que tem de acontecer para que se possa dizer correctamente de um objecto que este está mordiscado. É natural que respondamos diferentemente a esta pergunta, se feita a propósito de (2): “Consiste em metade do pedaço estar mordiscado”. Contudo, respondemos do modo como fizemos originalmente se a mesma pergunta for feita, a propósito de (2), acerca da metade direita.

Afirmar a propósito de (2) que o pedaço de queijo está mordiscado não é, portanto, tão directo, nem exactamente o mesmo que dizer isto a propósito de (1). Referi-me a esta disparidade como uma diferença de “estatuto”. Seja lá isso ao certo o que for, é claramente a mesma diferença que existe, a respeito de ser visto, entre o tomate em VT e o tomate em VTa (cf. pp. 103–104). Há que notar que se nos perguntassem em VTa “Em que consiste X ver o tomate?” responderíamos naturalmente “Consiste em X ver a parte proximal da sua superfície”, mas se nos fizessem a mesma pergunta em VT, ou ao olharmos para um objecto físico diante de nós (antes de “constatar” o facto-Q) responderíamos naturalmente à pergunta por ostensão, erguendo, por exemplo, um tomate diante do nariz do indagador, dizendo “Eis o que é ver um tomate”. Só após o “constatar” parecerá que ver o objecto físico envolve ver uma subopção do mesmo.

Será simplesmente verdade que em (2) o pedaço de queijo ele mesmo está mordiscado? Ao dizer que está, estaremos meramente a reportar um facto? Não haverá algo estranho na pergunta “O pedaço de queijo está mordiscado?” feita a propósito de (2) (ou de (3))? Considere esta série de perguntas: “O pedaço de queijo está mordiscado?”, acerca de (1). “Sim” (directamente). “A metade esquerda está mordiscada?”, acerca de (2) “Não” (directamente). “A metade direita está mordiscada?”, acerca de (2). “Sim” (directamente). “O pedaço de queijo está mordiscado?”, acerca de (2). Não parece esta pergunta algo estranha? Não hesitamos? A pergunta não parece apropriada em (2) e, na verdade, não o é. Hesitamos porque responder à pergunta afirmativamente ou negativamente implica termos de dizer que um objecto em um certo contexto está ou não mordiscado, quando, na verdade, não sucede uma coisa nem outra. Reconhecemos que o pedaço em (2) de algum modo não pertence à classe dos A s que estão mordiscados, embora, por outro lado, tampouco pertença à classe dos A s que não estão. Mas por que razão acabamos nesta terra de ninguém? Tome-se outro exemplo. Em (2) não hesitamos dizer que a metade direita está mordiscada; porém, hesitamos se nos perguntam isso a propósito de (3). Não há uma diferença física entre (2) e (3). A diferença crucial é que em (2) a metade direita é uma porção unitária, ao passo que em (3) é um composto de unidades. “Estar mordiscada ”¹⁰ aplica-se somente a unidades. O termo não foi concebido para se aplicar, afirmativa ou negativamente, a compostos de unidades como a metade direita em (3) e o pedaço de queijo em (2). Assim, se, sucumbindo à pressão de dizer ou que o pedaço de queijo em (2) está, ou que não está, mordiscado, dissermos que está, reconhecemos, não obstante, que há algo correcto em responder, ao invés, que na verdade não está mordiscado. Esta resposta negativa sublinha que o pedaço de queijo no contexto (2) não é inteiramente como um A ao qual “estar mordiscado” se aplica. Se consideramos que um composto de unidades (como o queijo em (2)) está mordiscado, temos então em mãos uma diferença a articular, e, ao procurar fazê-lo, damos connosco falando em coisas desconcertantes como estatutos ou modos de ter sido mordiscado. Não há dois “modos”, nem um “estatuto”, melhor ou pior, de ter sido mordiscado, até que tenhamos criado o “estatuto” inferior ou o segundo “modo”, forçando a aplicação de “mordiscado” a não unidades. Por fim, somente há que explicar um A ter sido mordiscado em termos de uma das suas porções ter sido mordiscada quando este A, uma vez mais, é um composto de unidades e, portanto, não é, seja como for, um membro do clube.

Concluo, assim, que há um tipo importante de incompatibilidade entre A estar mordiscada e o mesmo suceder com uma porção de A. O conceito de “estar mordiscada” tem as seguintes características especiais:

a) A expressão “estar mordiscada” apenas se aplica a A quando A é uma unidade. Porém, uma parte essencial de A ser uma unidade é não haver porções de A que são fixadas como unidades relevantes. Assim, quando “estar mordiscada” se aplica a A não há tal coisa como uma porção de A mordiscada.

b) Há uma porção de A mordiscada somente quando subporções de A são unidades. Que porção está mordiscada depende não apenas de condições físicas, mas também de que subporções são unidades. Assim, em circunstâncias nas quais há tal coisa como uma porção de A mordiscada, A não é uma unidade, mas um composto de unidades e, portanto, “mordiscada” nem se aplica nem deixa de se aplicar ao próprio A.

A qualquer conceito que tenha estas propriedades chamarei conceito unitário.¹¹

IV

Suponhamos, por enquanto, que “ver” é também um conceito unitário. Se assim é, então a verdade (ou antes, alguma da verdade) acerca da posição do filósofo deixa-se formular nas seguintes proposições:

1. O “facto-Q” não é um facto. Seria verdade que normalmente não podemos ver de um objecto físico senão parte da sua superfície somente se sucedesse de na maioria dos contextos (contextos quotidianos, normais) a porção proximal da superfície fosse fixada como uma das unidades relevantes. Porém, isto obviamente não sucede. É verdade que normalmente não podemos ver o lado oposto nem o interior de um objecto físico, mas, se “ver” é um conceito unitário, isto não significa que, portanto, não podemos ver do objecto senão a parte proximal da sua superfície. Considere os casos (2) e (3) uma vez mais (p. 106). Em (2), a metade direita está mordiscada, mas em (3) somente a quarta parte direita, ainda que em (2), tal como em (3), a segunda quarta parte a partir da direita não está ela mesma mordiscada. Que uma porção particular s de A não está ela mesma mordiscada não significa por si que não mais do que A -menos-s de A está mordiscada, a menos que s seja uma unidade relevante. Uma porção s que não está ela mesma mordiscada pode ser incluída na quantidade de A (apropriadamente) mordiscada.

Tudo isto se aplica também a “ver”, se este é um conceito unitário. “Mais” do que parte da superfície do objecto físico pode ser vista, pelo mesmo tipo de razão que “mais” é mordiscado em (2) do que em (3). Quanto algo é visto dependerá em parte do tamanho das unidades.

2. Ao pensar que o “facto-Q” tem consequências paradoxais, o filósofo tem, em um certo sentido, razão. Naquelas circunstâncias em que é verdade que de um objecto físico não podemos ver senão parte da sua superfície, “ver” nem se aplica nem deixa de aplicar ao objecto físico ele mesmo. (Pois nesses contextos a porção proximal da superfície é uma unidade, o objecto físico ele mesmo não o é.)

Embora nas discussões sobre percepção se ouça amiúde dizer ser trivialmente verdadeiro que ver um objecto físico envolve ver parte da sua superfície, alguns filósofos pensam, pelo contrário, que isto representa uma descoberta surpreendente, e que daí resulta que o nosso ver objectos físicos não corresponde às expectativas do senso comum. Se “ver” é um conceito unitário, então estes filósofos têm, mais uma vez, em um certo sentido, razão. O comum ver de um objecto físico não envolve ver parte da sua superfície (ou qualquer subporção dele), pois quando A é visto não há tal coisa como uma porção de A vista. Esse ver de um objecto físico que de facto envolve ver parte da sua superfície é a criação do próprio filósofo, o resultado de aplicar “ver” ao objecto físico em VTa, ou seja, ao objecto físico quando este é um composto de unidades. (A natureza de VTa é suplementarmente discutida em (3), mais adiante.) Este ver de um objecto físico, que é o único possível de um tal objecto quando é verdade que do objecto físico não podemos ver senão parte da sua superfície, é inferior ao ver comum.

3. Finalmente, o que sucede realmente, se “ver” é um conceito unitário, quando “constatamos” o “facto-Q”? Em VT nenhuma porção do tomate é fixa como unidade relevante; o próprio tomate é a unidade. Porém, em VTa, ou seja, quando o “facto-Q” foi “assinalado”, o próprio tomate não é mais uma unidade, pois uma porção da sua superfície é demarcada e, por assim dizer, colocada diante de nós para que a consideremos. Evidentemente, os outros modos de “constatar” o facto-Q (ver p. 105) realizam a mesma mudança de unidades. O “constatar” tem, no entanto, uma conexão íntima com o “facto-Q”. Em VT (ou quando, digamos, se observa um objecto físico no gabinete, sobre a secretária) não há tal coisa como uma quantidade do objecto físico vista. “Constatar” o “facto-Q” altera esta situação, exactamente na medida necessária para que do objecto físico não possamos ver senão parte de sua superfície. Assim, se “ver” é um conceito unitário, quando “constatamos” o “facto-Q” vemos qual é a nossa situação perceptual quando é verdade que de um objecto físico não podemos ver senão parte da sua superfície.

É interessante que este “constatar” seja, excepto quando usado em conexão com conceitos unitários, precisamente o que aparenta ser, e, quando usado em conexão com conceitos unitários, precisamente o que aparenta ser quando o facto “constatado” ou “assinalado” em uma situação é realmente um facto dessa situação.

É assim, portanto, que funciona a averiguação de superfície se “ver” é um conceito unitário. A questão é, evidentemente, se “ver” é ou não um conceito unitário.

O género de considerações aduzidas para mostrar que “estar mordiscada” é um conceito unitário, ainda que sejam adequadas a esse propósito, não servem para mostrar que “ver” é um tal conceito, a menos que, independentemente dessas considerações, possamos ver que o “facto-Q” não é um facto. Pois as nossas conclusões acerca de “mordiscada” tinham por base essencialmente “o que diríamos” em certas situações, e não vejo como se pode concluir justificadamente apenas com base em tais dados que é errado assentir ao facto-Q. Permita-se-me explicar. Suponhamos, por exemplo, que iniciamos a nossa análise de “ver” considerando os análogos para “ver” dos casos (1), (2) e (3) (p. 106). VT seria um análogo de (1), e, então, os análogos de (2) e (3) seriam construídos a partir de VT como (2) e (3) o são a partir de (1). Agora, se nos perguntassem, a propósito do análogo de (2), “Quanto do tomate pode X ver?”, responderíamos naturalmente, “Apenas a metade direita”, e, caso nos perguntassem o mesmo com referência ao análogo de (3), “Apenas a quarta parte direita”. Todavia, o que dizemos nestes casos tornaria claro que a porção de um objecto que é vista depende de que subporções são fixas como as porções unitárias relevantes (e, portanto, esclareceria que o “facto-Q” não é um facto) apenas se for absolutamente claro que as nossas respostas são, por assim dizer, patentemente correctas em vez de correctas apenas em uma certa maneira de falar ou para fins pragmáticos. Não tivemos de nos preocupar em mostrar isto quando considerávamos “mordiscada” pois não tínhamos razão alguma nesse caso para pensar que as nossas respostas poderiam estar correctas apenas em uma certa maneira de falar, ao passo que o forte apelo da crença no facto-Q constitui uma razão poderosa no caso de “ver”. Duvido de que considerar exemplos adicionais de “o que diríamos” em contextos particulares bastasse para superar o apelo desta crença e assim tornar claro que o que diríamos nesses casos está patentemente correcto.

É necessário um ataque directo ao facto-Q. De modo a preparar este ataque, examinemos agora directamente a averiguação de superfície.

O que sucede realmente na averiguação de superfície? Há três possibilidades. (1) O “facto-Q” é um facto. “Constatar” este facto é apenas constatar um facto previamente ignorado. (2) O “facto-Q” não é um facto. “Constatar” este “facto” altera a situação original — VT, ou o seu análogo na primeira pessoa —, e produz uma situação em que é verdade que do objecto físico não podemos ver senão uma porção da sua superfície. Que haja ainda uma terceira possibilidade é devido ao facto de que ao “constatar” o “facto-Q” fazemos duas coisas. (i) Focamo-nos numa porção da superfície do objecto físico, demarcando-a. (ii) Tomamos esta porção demarcada quando consideramos o que é de facto a verdade acerca de o próprio objecto físico poder ou não ser visto. (3) O “facto-Q” é um facto. Todavia, podemos ver objectos físicos apenas porque comummente o facto-Q não é tomado em consideração quando determinamos o que pode ser visto. Embora (i) possa ser legítima, sendo talvez apenas uma parte de atender ao facto-Q, (ii) não o é. Pois ao fazer (ii) alteramos a situação original — VT ou o seu análogo na primeira pessoa —, produzindo uma situação em que o facto-Q tem de ser tomado em consideração quando determinamos o que pode ser visto. A força desta terceira possibilidade é posta a nu constatando que quando o facto (inegável) de que o tomate tem uma fina membrana exterior é assinalado em VT, a posição perceptual de X fica pior, e quase exactamente do mesmo modo que quando o facto-Q é assinalado em VT.

Argumentarei agora que (1) e (3) devem ser rejeitadas. Consideremos primeiro (3). Quando, no análogo da primeira pessoa de VT, afirmamos “Não posso ver do objecto físico senão a porção próximal da sua superfície”, conseguimos dizer o que queríamos dizer e ver em que consiste ser verdade o que afirmamos somente quando demarcamos esta porção da superfície. (Compare-se proferir estas palavras sem demarcar esta porção e posteriormente enquanto as demarcamos.) Mas quando de facto queremos dizer o que dizemos, vemos que para ser verdade o que afirmamos, é necessário que o nosso ver abarque, por assim dizer, esta porção da superfície e somente esta porção. Quando cessamos de demarcar esta porção, o objecto físico volta a ser uma unidade e, aparentemente, passamos a estar numa posição perceptual diferente, pois agora o nosso ver parece abarcar o próprio objecto físico; a porção próxima da superfície não é agora abarcada per se mas incluída em um objecto que é abarcado per se. ¹² Esta posição perceptual é aquela em que nos encontrávamos, ou achávamos que nos encontrávamos, quando afirmámos, no início da averiguação de superfície, que podíamos ver o objecto físico. É imediatamente óbvio que ser verdade que vemos o objecto físico consiste em suceder que nos encontramos nesta posição perceptual. Assim, constatamos, contrariamente a (3), que não só a relevância mas também a verdade de “Não podemos ver do objecto físico senão a posição próxima da sua superfície” é incompatível com a verdade de “Podemos ver o objecto físico”. Somente se demarcamos a porção relevante da superfície e a tomamos como demarcada ((i) e (ii)) é que criamos o estado de coisas em que é verdade que do objecto físico não vemos senão a porção próxima da sua superfície.

Segue-se que se o “facto-Q” é um facto, a nossa posição perceptual é pior do que supõe o senso comum. Esta é em si mesma uma boa razão para considerar o “facto-Q” com (pelo menos alguma) suspeição. Contudo, há, creio, uma razão decisiva para rejeitar o “facto-Q” (e portanto a primeira possibilidade). A razão para aceitar o facto-Q é que quando demarcamos a porção próxima da superfície do objecto físico é patentemente verdade que não podemos ver do objecto senão esta porção. Assim, termos ou não uma boa razão para aceitar o facto-Q depende de termos ou não uma boa razão para acreditar que esta “demarcação” é directa, ou seja, apenas parte de constatar um facto. Porém, uma análise de “ver”, exactamente paralela ao estudo de “estar mordiscada”, revela que “ver” é um conceito unitário. Especificamente, revela que esta “demarcação”, se aplicada a VT — ou ao seu análogo na primeira pessoa — a qualquer subporção s (ou antes, a qualquer s que oculte completamente o resto do objecto físico), faz que seja verdade que do objecto físico não podemos ver senão s, e, consequentemente, que nem é verdadeiro nem falso que o próprio objecto físico seja visto. Assim, para ter uma razão para aceitar o facto-Q, deveríamos ter uma razão para defender, contra tal estudo, que essa “demarcação” é, em uma certa aplicação, ou seja, quando aplicada à porção próxima da superfície, directa. Mas que razão há para supor tal coisa?

Uma última palavra: há contextos em que A é visto e uma porção de A é vista. Este facto, contudo, não significa que A ser visto e uma porção de A ser vista não são mutuamente incompatíveis, pois pode-se mostrar (embora não no espaço dado ao presente artigo) que em tais contextos A é por vezes tratado como uma unidade, por vezes como um composto de unidades, e que é verdade que A é visto somente quando A é tratado como uma unidade e verdade que uma porção de A é vista somente quando A é tratado como um composto de unidades.¹³

Notas

1. Por exemplo: C. D. Broad, The Mind and Its Place in Nature, Nova Iorque, 1937, esp. pp. 148–151; G. E. Moore, Some Main Problems of Philosophy, Londres 1953, esp. 33–34.

   Esta seria também a posição alcançada no seguinte argumento que Descartes apresenta na Segunda Meditação, se esse argumento fosse levado à sua conclusão lógica:

   “Daqui devo concluir que conhecia a cera por meio da visão e não apenas pela intuição da mente; a menos que por acaso me lembre de que, ao olhar de uma janela e dizer que vejo homens passando na rua, na verdade não os vejo, mas infiro que são homens o que vejo, (...) E no entanto o que vejo da janela senão chapéus e capas que podem cobrir autómatos? Porém, ajuízo que se tratam de homens.”↩︎

2. Essas perspectivas têm tão ampla aceitação que poucos filósofos se dão ao trabalho de as pôr no papel. Mas veja-se, por exemplo: Martin Lean, Sense Perception and Matter, Nova Iorque 1953, esp. pp. 68–69.

   No seu livro recente, também Chisholm defendeu que o filósofo alcança a sua posição devido ao mencionado “pressuposto”.

   Roderick M. Chisholm, Perceiving: A Philosophical Study, Ithaca, Nova Iorque 1957, esp. pp. 153–156.↩︎

3. Ver acima, nota I, p. 1.↩︎
4. G. E. Moore, Some Main Problems of Philosophy, Londres 1953, p. 34.↩︎
5. C. D. Broad, The Mind and Its Place in Nature, Nova Iorque 1937, p. 149.↩︎
6. Que isto é o que achamos após “assinalar o facto-Q” poderia ter sido evidenciado mais directamente pela comparação entre VT, VTa e um caso em que a porção de superfície em causa é destacada e movida ligeiramente na direcção de X, desde que não hesitássemos em tomar parte na ficção de que o último caso mencionado faz sentido.↩︎
7. N. do T. Ver notas 9 e 10.↩︎
8. A metade é a metade original (antes de ser mordiscada).↩︎
9. O contraste entre “está mordiscada” e “foi mordiscada” pretende captar a diferença entre o inglês nibbled at e nibbled up, que é a diferença entre algo “ter mordiscadas” e ter sido consumido por esse processo. Uma solução para obviar ao facto de em português não termos uma expressão verbal composta correspondente a qualquer dos phrasal verbs em inglês: nibbled at e nibbled up. Assentamos assim a distinção na diferença entre formar a expressão com o verbo estar ou com o verbo ser. Em todo o caso, nibbled up ocorre apenas uma vez em todo o texto e só noutras duas ocasiões é preciso pensar explicitamente em nibbled at no contraste com nibbled up — ver nota 10. N. do T. ↩︎
10. Mais uma vez, nibbled at — aqui o contraste é com “foi mordiscada” (nibbled up ). Ver nota 9. N. do T. ↩︎
11. Há possíveis excepções a (a) e (B) que, todavia, não têm de nos preocupar aqui.

    (1) Não argumentei directamente que “mordiscada” não se aplica a uma não unidade A como a quarta parte direita no caso (2), p. 106.

    (2) Talvez se deva dizer de um composto de unidades que está mordiscado quando cada uma das suas unidades o foi.

    (3) Quando não houve de todo qualquer mordiscada em ligação com A, então é simultaneamente verdade que A não está mordiscada e que nenhuma porção de A está mordiscada.↩︎

12. Seria desejável, evidentemente, exprimir estes factos de uma maneira não tão metafórica, mas não procurarei fazê-lo aqui.↩︎
13. Quero agradecer ao American Council of Learned Societies a bolsa de estudo que me proporcionou um período livre das actividades lectivas, parcialmente ocupado pela redacção deste artigo.↩︎